参考算导第三版第16章 贪心算法
文章目录
求解最优化问题的算法,通常需要经过一系列的步骤,在每个步骤都面临多种选择。对于许多最优化问题,使用动态规划算法来求最优解有些小题大做了,可以用更简单、更高效的算法。贪心算法 greedy algorithm 就是这样的算法,它在每一步都做出当时看起来最佳的选择。也就是说,它总是做出局部最优的选择,寄希望这样的选择能导致全局最优解。这里介绍一些贪心算法能找到最优解的最优化问题。学习贪心之前,应该学习动态规划(算导第15章,尤其是算导15.3节)。
贪心算法并不保证得到最优解,但对很多问题确实可以求得最优解。
- 首先在(算导16.1节)介绍一个简单但非平凡的问题——活动选择问题,这是一个可以用贪心算法求得最优解的问题。首先考虑用动态规划解决这个问题,然后证明一直做出贪心选择,就可以得到最优解,从而得到一个贪心算法。
- (算导16.2节)回顾贪心方法的基本要素,并给出一个直接的方法,可用来证明贪心算法的正确性。
- (算导16.3节)提出贪心技术的一个重要应用:设计数据压缩编码(Huffman 编码)。
- (算导16.4节)讨论一种称为拟阵
matroid的组合结构的理论基础,贪心算法总是能获得这种结构的最优解。 - (算导16.5节)将拟阵应用于单位时间任务调度问题,每个任务均有截止时间和超时惩罚。
贪心方法是一种强有力的算法设计方法,可以很好地解决很多问题。利用贪心策略设计的算法,包括最小生成树(算导第23章)、单源最短路径的 Dijkstra 算法(算导第24章)以及集覆盖问题的 C h v a ˊ t a l \mathit{Chv\acute{a}tal} Chvaˊtal 贪心启发式算法(算导第35章),建议一起结合学习。
1. 活动选择问题
第一个例子是一个调度「竞争共享资源的多个活动」的问题,目标是选出一个最大的互相兼容的活动集。假定有一个
n
n
n 个活动 activity 的集
S
=
{
a
1
,
a
2
,
…
,
a
n
}
S = \{ a_1, a_2, \dots, a_n\}
S={a1,a2,…,an} ,这些活动使用同一个资源(例如一间教室),而这个资源在某个时刻只能供一个活动使用。
每个活动
a
i
a_i
ai 都有一个开始时间
s
i
s_i
si 和一个结束时间
f
i
f_i
fi ,其中
0
≤
s
i
<
f
i
<
∞
0 \le s_i < f_i < \infin
0≤si<fi<∞ 。如果被选中,任务
a
i
a_i
ai 发生在半开时间区间
[
s
i
,
f
i
)
[s_i, f_i)
[si,fi) 期间。如果两个活动
a
i
a_i
ai 和
a
j
a_j
aj 满足
[
s
i
,
f
i
)
[s_i, f_i)
[si,fi) 和
[
s
j
,
f
j
)
[s_j, f_j)
[sj,fj) 不重叠,则称它们是兼容的 compatible 。也就是说,若
s
i
≥
f
j
s_i \ge f_j
si≥fj 或
s
j
≥
f
i
s_j \ge f_i
sj≥fi ,则
a
i
a_i
ai 和
a
j
a_j
aj 是兼容的。在活动选择问题中,我们希望选出一个最大兼容活动集。
假定活动已按结束时间的单调递增顺序排序(稍后会看到这一假设的好处): f 1 ≤ f 2 ≤ f 3 ≤ ⋯ ≤ f n − 1 ≤ f n (16.1) f_1 \le f_2 \le f_3 \le \dots \le f_{n-1} \le f_n \tag{16.1} f1≤f2≤f3≤⋯≤fn−1≤fn(16.1)
例如,考虑下面的活动集
S
S
S :

对于这个例子,子集
{
a
3
,
a
9
,
a
11
}
\{ a_3, a_9, a_{11} \}
{a3,a9,a11} 由相互兼容的活动组成,但它不是一个最大集,因为子集
{
a
1
,
a
4
,
a
8
,
a
11
}
\{ a_1, a_4, a_8, a_{11} \}
{a1,a4,a8,a11} 更大。实际上,
{
a
1
,
a
4
,
a
8
,
a
11
}
\{ a_1, a_4, a_8, a_{11} \}
{a1,a4,a8,a11} 是一个最大兼容活动子集,另一个最大子集是
{
a
2
,
a
4
,
a
9
,
a
11
}
\{ a_2, a_4, a_9, a_{11} \}
{a2,a4,a9,a11} 。
下面分几个步骤来解决这个问题。
- 我们可以通过动态规划方法,将这个问题分为两个子问题,然后将两个子问题的最优解整合成原问题的一个最优解。在确定该将哪些子问题用于最优解时,要考虑几种选择。
- 稍后会发现,贪心算法只需要考虑一个选择(即贪心的选择),在做贪心选择时,子问题之一必是空的,因此只留下一个非空子问题。
- 基于这些观察,我们将找到一种递归贪心算法来解决活动调度问题,并将递归算法转换为迭代算法、以完成贪心方法的过程。
虽然本节介绍的步骤比典型的贪心算法的设计过程更为复杂,但它们说明了贪心算法和动态规划之间的关系。
1.1 活动选择问题的最优子结构
我们容易验证,活动选择问题具有最优子结构性质。令 S i j S_{ij} Sij 表示在 a i a_i ai 结束之后开始、且在 a j a_j aj 开始之前结束的那些活动的集。假定我们希望求 S i j S_{ij} Sij 的一个最大的相互兼容的活动子集,进一步假定 A i j A_{ij} Aij 就是这样一个子集,包含活动 a k a_k ak 。由于最优解包含活动 a k a_k ak ,我们得到两个子问题:寻找 S i k S_{ik} Sik 中的兼容活动(在 a i a_i ai 结束之后开始、且在 a k a_k ak 开始之前结束的那些活动)以及寻找 S k j S_{kj} Skj 中的兼容活动(在 a k a_k ak 结束之后开始、且在 a j a_j aj 开始之前结束的那些活动)。
令 A i k = A i j ∩ S i k A_{ik} = A_{ij} \cap S_{ik} Aik=Aij∩Sik 和 A k j = A i j ∩ S k j A_{kj} = A_{ij} \cap S_{kj} Akj=Aij∩Skj ,这样 A i k A_{ik} Aik 包含 A i j A_{ij} Aij 中那些在 a k a_k ak 开始之前结束的活动, A k j A_{kj} Akj 包含 A i j A_{ij} Aij 中那些在 a k a_k ak 结束之后开始的活动。因此,我们有 A i j = A i k ∪ { a k } ∪ A k j A_{ij} = A_{ik} \cup \{ a_k \} \cup A_{kj} Aij=Aik∪{ak}∪Akj ,而且 S i j S_{ij} Sij 中最大兼容任务子集 A i j A_{ij} Aij 包含 ∣ A i j ∣ = ∣ A i k ∣ + ∣ A k j ∣ + 1 |A_{ij}| = | A_{ik} | + |A_{kj} | + 1 ∣Aij∣=∣Aik∣+∣Akj∣+1 个活动。
我们仍然用剪切-粘贴法 cut-and-paste 证明,最优解
A
i
j
A_{ij}
Aij 必然包含两个子问题
S
i
k
S_{ik}
Sik 和
S
k
j
S_{kj}
Skj 的最优解。否则,如果可以找到
S
k
j
S_{kj}
Skj 的一个兼容活动子集
A
k
j
′
A_{kj}'
Akj′ ,满足
∣
A
k
j
′
∣
>
∣
A
k
j
∣
|A_{kj}' | > |A_{kj} |
∣Akj′∣>∣Akj∣ ,则可以将
A
k
j
′
A_{kj}'
Akj′ 而不是
A
k
j
A_{kj}
Akj 作为
S
i
j
S_{ij}
Sij 的最优解的一部分。这样就构造出一个兼容活动集,其大小
∣
A
i
k
∣
+
∣
A
k
j
′
∣
+
1
>
∣
A
i
k
∣
+
∣
A
k
j
∣
+
1
=
∣
A
i
j
∣
|A_{ik} | + | A_{kj}' | + 1 > |A_{ik} | + | A_{kj} |+ 1 = | A_{ij}|
∣Aik∣+∣Akj′∣+1>∣Aik∣+∣Akj∣+1=∣Aij∣ ,与
A
i
j
A_{ij}
Aij 是最优解的假设矛盾。对子问题
S
i
k
S_{ik}
Sik 类似可证。
这样刻画活动选择问题的最优子结构,意味着我们可以用动态规划方法求解活动选择问题。如果用 c [ i , j ] c[i, j] c[i,j] 表示集 S i j S_{ij} Sij 的最优解的大小,则可得递归式: c [ i , j ] = c [ i , k ] + c [ k , j ] + 1 c[i, j] = c[i, k] + c[k, j] +1 c[i,j]=c[i,k]+c[k,j]+1
当然,如果不知道 S i j S_{ij} Sij 的最优解包含活动 a k a_k ak ,就需要考察 S i j S_{ij} Sij 中所有活动,寻找哪个活动可获得最优解。于是: c [ i , j ] = { 0 若 S i j = ∅ max a k ∈ S i j { c [ i , k ] + c [ k , j ] + 1 } 若 S i j ≠ ∅ (16.2) c[i, j] = \begin{cases} 0 \quad &若 S_{ij} = \varnothing \\ \displaystyle \max_{a_k \in S_{ij}} \{ c[i, k] +c[k, j] + 1 \} \quad &若S_{ij} \ne \varnothing \end{cases} \tag{16.2} c[i,j]=⎩⎨⎧0ak∈Sijmax{c[i,k]+c[k,j]+1}若Sij=∅若Sij=∅(16.2)
于是,接下来可以设计一个带备忘机制的递归算法,或者使用自底向上法填写表项。但我们可能忽略了活动选择问题的另一个重要性质,而这一性质可以极大地提高问题求解速度。
1.2 贪心选择
假如我们无需求解所有子问题,就可以选择出一个活动加入到最优解,将会怎样?这将使我们省去递归式 ( 16.2 ) (16.2) (16.2) 中固有的考查所有选择的过程。实际上,对于活动选择问题,我们只需考虑一个选择:贪心选择。
对于活动选择问题,什么是贪心选择?直观上,我们应该选择这样一个活动,选出它后剩下的资源,应能被尽量多的其他任务所用。现在考虑可选的活动,其中必然有一个最先结束。因此,直觉告诉我们,应该选择 S S S 中最早结束的活动,因为它剩下的资源、可供它之后尽量多的活动使用(如果 S S S 中最早结束的活动有多个,我们可以任选其中一个)。换句话说,由于活动已按结束时间单调递增的顺序排序,贪心选择就是活动 a 1 a_1 a1 。选择最早结束的活动并不是本问题唯一的贪心选择方法,还可(算导练习16.1-3要求)设计其他贪心选择方法。
当做出贪心选择后,只剩下一个子问题需要我们求解:寻找在 a 1 a_1 a1 结束后开始的活动。为什么不需要考虑在 a 1 a_1 a1 开始前结束的活动呢?因为 s 1 < f 1 s_1 < f_1 s1<f1 且 f 1 f_1 f1 是最早结束的活动,所以不会有活动的结束时间早于 s 1 s_1 s1 。因此,所有与 a 1 a_1 a1 兼容的活动、都必须在 a 1 a_1 a1 结束之后开始。
而且,我们已经证明,活动选择问题具有最优子结构性质。令 S k = { a i ∈ S ∣ s i ≥ f k } S_k = \{ a_i \in S \mid s_i \ge f_k \} Sk={ai∈S∣si≥fk} 为在 a k a_k ak 结束后开始的任务集。当我们做出贪心选择,选择了 a 1 a_1 a1 后,剩下的 S 1 S_1 S1 是唯一需要求解的子问题(我们有时用 S k S_k Sk 表示子问题而不是活动集。根据上下文,可以清楚判定 S k S_k Sk 表示一个活动集、还是以该活动集为输入的子问题)。最优子结构性质告诉我们,如果 a 1 a_1 a1 在最优解中,那么原问题的最优解由活动 a 1 a_1 a1 和子问题 S 1 S_1 S1 中所有活动组成。
现在还剩下一个大问题:我们的直觉是正确的吗?贪心选择——最早结束的活动——总是最优解的一部分吗?下面的定理证明了这一点。
定理16.1 考虑任意非空子问题
S
k
S_k
Sk ,令
a
m
a_m
am 是
S
k
S_k
Sk 中结束时间最早的活动,则
a
m
a_m
am 在
S
k
S_k
Sk 的某个最大兼容活动子集中。
证明:令
A
k
A_k
Ak 是
S
k
S_k
Sk 的一个最大兼容活动子集,且
a
j
a_j
aj 是
A
k
A_k
Ak 中结束时间最早的活动。
- 若 a j = a m a_j = a_m aj=am ,则已经证明 a m a_m am 在 S k S_k Sk 的某个最大兼容活动子集中。
- 若 a j ≠ a m a_j \ne a_m aj=am ,令集 A k ′ = A k − { a j } ∪ { a m } A_k' = A_k - \{ a_j \} \cup \{ a_m \} Ak′=Ak−{aj}∪{am} ,即将 A k A_k Ak 中的 a j a_j aj 替换为 a m a_m am 。 A k ′ A_k' Ak′ 中的活动都是不相交的,因为 A k A_k Ak 中的活动都是不相交的, a j a_j aj 是 A k A_k Ak 中结束时间最早的活动,而 f m ≤ f j f_m \le f_j fm≤fj 。由于 ∣ A k ′ ∣ = ∣ A k ∣ |A_k'| = |A_k| ∣Ak′∣=∣Ak∣ ,因此得出结论 A k ′ A_k' Ak′ 也是 S k S_k Sk 的一个最大兼容活动子集,且它包含 a m a_m am 。 ■ \blacksquare ■
因此我们看到,虽然可以用动态规划方法求解活动选择问题,但并不需要这样做(此外,我们并未检查活动选择问题是否具有重叠子问题性质)。相反,我们可以反复选择最早结束的活动,保留与此活动兼容的活动,重复这一过程,直到不再有剩余活动。而且,因为我们总是选择最早结束的活动,所以选择的活动的结束时间必然是严格递增的。我们只需按结束时间的单调递增顺序处理所有活动,每个活动只考察一次。
求解活动选择问题的算法,不必像基于表格的动态规划算法那样、自底向上地进行计算。相反,可以自顶向下进行计算——选择一个活动放入最优解,然后对剩余的子问题(包含与已选择的活动兼容的活动)进行求解。贪心算法通常都是这种自顶向下的设计:做出一个选择,然后求解剩下的那个子问题,而不是自底向上地求解出很多子问题,然后再做出选择。
1.3 递归贪心算法
我们已经看到,如何绕过动态规划方法、而使用自顶向下的贪心算法来求解活动选择问题,现在可以设计一个直接的递归过程来实现贪心算法。过程 RECURSIVE-ACTIVITY-SELECTOR 为两个数组
s
s
s 和
f
f
f ,表示活动的开始和结束时间,下标
k
k
k 指出要求解的子问题
S
k
S_k
Sk ,以及问题规模
n
n
n 。它返回
S
k
S_k
Sk 的一个最大兼容活动集。
我们假定输入的
n
n
n 个活动已经按结束时间的单调递增顺序排列好(公式
(
16.1
)
(16.1)
(16.1) )。如果未排好序,我们可在
O
(
n
log
n
)
O(n\log n)
O(nlogn) 时间内对它们进行排序,结束时间相同的活动可以任意排列。为了方便算法初始化,我们添加一个虚拟活动
a
0
a_0
a0 ,其结束时间
f
0
=
0
f_0 = 0
f0=0 ,这样子问题
S
0
S_0
S0 就是完整的活动集
S
0
S_0
S0 。求解原问题即可调用 RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n) 。
RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n)
m = k + 1
while m <= n and s[m] < f[k] // find the first activity in Sk to finish
m = m + 1
if m <= n
return { am } ∪ RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n)
else return ∅
图16-1显示了算法的执行过程。在一次递归调用 RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n) 的过程中,第
2
∼
3
2 \sim 3
2∼3 行 while 循环查找
S
k
S_k
Sk 中最早结束的活动。循环检查
a
k
+
1
,
a
k
+
2
,
…
,
a
n
a_{k+1}, a_{k+2}, \dots, a_n
ak+1,ak+2,…,an ,直到找到第一个与
a
k
a_k
ak 兼容的活动
a
n
a_n
an 。此活动满足
s
m
≥
f
k
s_m \ge f_k
sm≥fk 。如果循环因为查找成功而结束,第
5
5
5 行返回
{
a
m
}
\{ a_m \}
{am} 与「 RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n) 返回的
S
m
S_m
Sm 的最大兼容活动子集」的并集。循环也可能因为
m
>
n
m > n
m>n 而终止,这意味着我们已经检查了
S
k
S_k
Sk 中所有活动,未找到与
a
k
a_k
ak 兼容者。在这种情况下,
S
k
=
∅
S_k = \varnothing
Sk=∅ ,因此第
6
6
6 行返回
∅
\varnothing
∅ 。

假定活动已经按结束时间排好序,则递归调用 RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n) 的运行时间为
Θ
(
n
)
\Theta(n)
Θ(n) ,我们稍后将证明这个结论。在整个递归调用过程中,每个活动被且只被第
2
2
2 行的 while 循环检查一次。特别地,活动
a
i
a_i
ai 在
k
<
i
k < i
k<i 的最后一次调用中被检查。
1.4 迭代贪心算法
我们可以很容易地将算法转换为迭代形式。过程 RECURSIVE-ACTIVITY-SELECTOR 几乎就是尾递归(算导思考题7-4):它以一个对自身的递归调用再接一次并集操作结尾。将一个尾递归过程改为迭代形式,通常是很直接的。实际上,某些特定语言的编译器可以自动完成这一工作。如前所述,RECURSIVE-ACTIVITY-SELECTOR 用来求解子问题
S
k
S_k
Sk ,即由最后要完成的活动组成的子问题 i.e., subproblems that consist of the last activities to finish(?)。
过程 GREEDY-ACTIVITY-SELECTOR 是过程 RECURSIVE-ACTIVITY-SELECTOR 的一个迭代版本。它也假定输入活动已按结束时间单调递增顺序排好序。它将选出的活动存入集
A
A
A 中,并将
A
A
A 返回调用者。
GREEDY-ACTIVITY-SELECTOR(s, f)
n = s.length
A = { a_1 }
k = 1
for m = 2 to n
if s[m] >= f[k]
A = A ∪ { a_m }
k = m
return A
过程执行如下。变量 k k k 记录了最近加入集 A A A 的活动的下标,它对应递归算法中的活动 a k a_k ak 。由于我们按结束时间的单调递增顺序处理活动, f k f_k fk 总是 A A A 中活动的最大结束时间。也就是说: f k = max { f i ∣ a i ∈ A } (16.3) \tag{16.3} f_k = \max \{ f_i \mid a_i \in A \} fk=max{fi∣ai∈A}(16.3)
第
2
∼
3
2 \sim 3
2∼3 行选择活动
a
1
a_1
a1 ,将
A
A
A 的初值设置为只包含此活动,并将
k
k
k 的初值设为此活动的下标。第
4
∼
7
4 \sim 7
4∼7 行的 for 循环查找
S
k
S_k
Sk 中最早结束的活动。循环依次处理每个活动
a
m
a_m
am ,
a
m
a_m
am 若与之前选出的活动兼容,则将其加入
A
A
A ,这样选出的
a
m
a_m
am 必然是
S
k
S_k
Sk 中最早结束的活动。为了检测活动
a
m
a_m
am 是否与
A
A
A 中所有活动都兼容,过程检查公式
(
16.3
)
(16.3)
(16.3) 是否成立,即检查活动的开始时间
s
m
s_m
sm 是否不早于最近加入到
A
A
A 中的活动的结束时间
f
k
f_k
fk 。如果活动
a
m
a_m
am 是兼容的,则第
6
∼
7
6 \sim 7
6∼7 行将其加入
A
A
A 中,并将
k
k
k 设置为
m
m
m 。GREEDY-ACTIVITY-SELECTOR(s, f) 返回的集
A
A
A 与 RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n) 返回的集完全相同。
与递归版本类似,在输入活动已按结束时间排序的前提下,GREEDY-ACTIVITY-SELECTOR 的运行时间为
Θ
(
n
)
\Theta(n)
Θ(n) 。
2. 贪心算法原理
贪心算法通过做出一系列选择、来求出问题的最优解。在每个决策点,它做出在当时看来最佳的选择。这种启发式策略并不保证总能找到最优解,但对有些问题确实有效,如活动选择问题。本节讨论贪心方法的一些一般性质。
(算导16.1节中)设计贪心算法的过程,比通常的过程繁琐一些,我们当时经历了如下几个步骤:
- 确定问题的最优子结构。
- 设计一个递归算法(对活动选择问题,我们给出了递归式 ( 16.2 ) (16.2) (16.2) ,但跳过了基于此递归式设计递归算法的步骤)。
- 证明,如果我们做出一个贪心选择,则只剩下一个子问题。
- 证明,贪心选择总是安全的(步骤 3 , 4 3, 4 3,4 的顺序可以调换)。
- 设计一个递归算法实现贪心策略。
- 将递归算法转换为迭代算法。
在这个过程中我们详细地看到了,贪心算法是如何以动态规划方法为基础的。例如,在活动选择问题中,我们首先定义了子问题 S i j S_{ij} Sij ,其中 i i i 和 j j j 都是可变的。然后我们发现,如果总是做出贪心选择,则可以将子问题限定为 S k S_k Sk 的形式。
换句话说,我们可以通过贪心选择来改进最优子结构,使得选择后只留下一个子问题。在活动选择问题中,我们可以一开始就将第二个下标去掉,将子问题定义为 S k S_k Sk 的形式。然后我们可以证明,贪心选择( S k S_k Sk 中最早结束的活动 a m a_m am )与剩余兼容活动集的最优解组合在一起,就会得到 S k S_k Sk 的最优解。
更一般地,我们可以按如下步骤设计贪心算法。
- 将最优化问题转换为这样的形式:对其作出一次选择后,只剩下一个子问题需要求解。
- 证明,做出贪心选择后,原问题总是存在最优解,即贪心选择总是安全的。
- 证明,做出贪心选择后,剩余的子问题满足性质:其最优解与贪心选择组合,即可得到原问题的最优解,这样就得到了最优子结构。
在剩余部分中,我们将使用这种更直接的设计方法。但应该知道,在每个贪心算法之下,几乎总有一个更繁琐的动态规划算法。
我们如何证明,一个贪心算法是否能求解一个最优化问题呢?并没有适合所有情况的方法,但贪心选择性质和最优子结构是两个关键要素。如果我们能够证明问题具有这些性质,就向贪心算法迈出了重要一步。
2.1 贪心选择性质
第一个关键要素是贪心选择性质 greedy-choice property :我们可以通过做出局部最优(贪心)选择来构造全局最优解。换句话说,当进行选择时,我们直接做出在当前问题中看来最优的选择,而不必考虑子问题的解。
这也是贪心算法与动态规划的不同之处:
- 在动态规划方法中,每个步骤都要进行一次选择,但选择通常依赖于子问题的解。因此,我们通常以一种自底向上的方法求解动态规划问题,先求解较小的子问题,然后是较大的子问题(我们也可以自顶向下求解,但需要备忘机制。当然,即使算法是自顶向下进行计算,我们仍然需要先求解子问题再进行选择)。
- 在贪心算法中,我们总是做出当时看来最佳的选择,然后求解剩下的唯一的子问题。贪心算法进行选择时可能依赖之前做出的选择,但不依赖任何将来的选择或是子问题的解。因此,与动态规划先求解子问题才能进行第一次选择不同,贪心算法进行第一次选择之前不求解任何子问题。
- 一个动态规划算法是自底向上进行计算的,而一个贪心算法通常是自顶向下的,进行一次又一次选择,将给定问题实例变得更小。
当然,我们必须证明,每个步骤都做出贪心选择、能生成全局最优解。如定理16.1所示,这种证明首先考查某个子问题的最优解,然后用贪心选择替换某个其他选择来修改此解,从而得到一个相似但更小的子问题。
如果进行贪心选择时、我们不得不考虑众多选择,通常意味着可以改进贪心选择,使其更为高效。例如,在活动选择问题中,假定我们已经将活动按结束时间单调递增顺序排好序,则对每个活动能只需处理一次。通过对输入进行预处理、或者使用适合的数据结构(通常是优先队列),我们通常可以使贪心选择更快速,从而得到更高效的算法。
2.2 最优子结构
如果一个问题的最优解包含其子问题的最优解,则称此问题具有最优子结构性质。此性质是能否应用动态规划和贪心方法的关键要素。还是以(算导16.1节的)活动选择问题为例,如果一个子问题 S i j S_{ij} Sij 的最优解包含活动 a k a_k ak ,那么它必然也包含子问题 S i k S_{ik} Sik 和 S k j S_{kj} Skj 的最优解。给定这样的最优子结构,我们可以得出结论,如果知道 S i j S_{ij} Sij 的最优解应该包含哪个活动 a k a_k ak ,就可以组合 a k a_k ak 以及「 S i k S_{ik} Sik 和 S k j S_{kj} Skj 的最优解中所有活动」来构造 S i j S_{ij} Sij 的最优解。基于对最优子结构的这种观察结果,我们就可以设计出递归式 ( 16.2 ) (16.2) (16.2) 来描述最优解值的计算方法。
当应用于贪心算法时,我们通常使用更为直接的最优子结构。如前所述,我们可以假定,通过对原问题应用贪心选择、即可得到子问题。我们真正要做的全部工作就是论证:将子问题的最优解与贪心选择组合在一起,就能生成原问题的最优解。这种方法隐含地对子问题使用了数学归纳法,证明了在每个步骤进行贪心选择、会生成原问题的最优解。
2.3 贪心对动态规划
由于贪心和动态规划都利用了最优子结构性质,我们可能会对一个可用贪心算法求解的问题设计一个动态规划算法,或者对实际上需要用动态规划求解的问题使用了贪心方法。为了说明两种方法之间的细微差别,我们研究一个经典最优化问题的两个变形。
- 0-1背包问题
0-1 knapsack problem是这样的:一个正在抢劫商店的小偷发现了 n n n 个商品,第 i i i 个商品价值 v i v_i vi 美元,重 w i w_i wi 磅, v i , w i v_i, w_i vi,wi 都是整数。这个小偷希望拿走价值尽量高的商品,但她的背包最多只能容纳 W W W 磅重的商品, W W W 是一个整数。她应该拿那些商品呢?(这个问题是0-1背包问题,因为对每个商品,小偷要么完整拿走,要么把它留下;她不能只拿走一个商品的一部分,或者把一个商品拿走多次)。 - 分数背包问题
fractional knapsack problem中,设定与0-1背包问题是一样的,但对每个商品,小偷可以拿走其一部分,而不是只能做出二元选择。
两个背包问题都具有最优子结构性质。
- 对0-1背包问题,考虑重量不超过 W W W 磅、且价值最高的负载。如果我们从该负载中移除物品 j j j ,则剩余负载必须是小偷可以从 n − 1 n - 1 n−1 个其他商品(不包括 j j j )中获取的、重量不超过 W − w j W - w_j W−wj 磅的最有价值的负载。
- 对于可比较的分数背包问题,考虑如果我们从最优负载中移除一个商品 j j j 的 w w w 磅重量,则剩余的负载必须是小偷可以从「 n − 1 n - 1 n−1 个其它商品加上 w j − w w_j - w wj−w 磅的商品 j j j 」中获取的、重量不超过 W − w W - w W−w 磅的最有价值的负载。
虽然两个问题相似,但我们用贪心策略可以求解分数背包问题,而不能求解0-1背包问题。为了求解分数背包问题,我们首先计算每个商品的每磅价值 v i w i \dfrac{ v_i } {w_i} wivi 。遵循贪心策略,小偷首先尽量多地拿走每磅价值最高的商品。如果该商品已全部拿走、而背包尚未满,她继续尽量多地拿走每磅价值第二高的商品,依此类推,直至达到重量上限 W W W 。因此,通过将商品按每磅价值排序,贪心算法的运行时间为 O ( n log n ) O(n\log n) O(nlogn) 。分数背包问题的贪心选择性质的证明,见(算导练习16.2-1)。
为了说明这一贪心策略对0-1背包问题无效,考虑图16-2(a)所示的问题实例。此例包含 3 3 3 个商品和一个能容纳 50 50 50 磅重量的背包,商品 1 , 2 , 3 1,2,3 1,2,3 分别重 10 , 20 , 30 10,20,30 10,20,30 磅,价值分别为 60 , 100 , 120 60,100,120 60,100,120 美元。因此,商品 1 , 2 , 3 1,2,3 1,2,3 的每磅价值分别为 6 , 5 , 4 6,5,4 6,5,4 美元。上述贪心策略会首先拿走商品 1 1 1 。但是如图16-2(b)的实例分析所示,最优解应该拿走商品 2 , 3 2, 3 2,3 、而留下商品 1 1 1 。拿走商品 1 1 1 的两种方案都是次优的。
但是如图16-2 c)所示,对于分数背包问题,上述贪心策略首先拿走商品
1
1
1 ,是可以生成最优解的。拿走商品
1
1
1 的策略对于0-1背包问题无效,是因为小偷无法装满背包,空闲空间降低了方案的有效每磅价值。在0-1背包问题中,当我们考虑是否将一个商品装入背包时,必须比较包含此商品的子问题的解、与不包含它的子问题的解,然后才能做出选择。这会导致大量的重叠子问题——动态规划的标识,(算导16.2-2要求)证明,可以用动态规划方法求解0-1背包问题。

3. 哈夫曼编码
哈夫曼编码可以很有效地压缩数据,通常可以节省 20 % ∼ 90 % 20\% \sim 90\% 20%∼90% 的空间,具体压缩率依赖于数据的特性。我们将待压缩数据看做字符序列。根据每个字符的出现频率,哈夫曼贪心算法构造出字符的最优二进制表示。
假设我们希望压缩一个
10
10
10 万个字符的数据文件。图16-3给出了文件中出现的字符和它们的出现频率。即文件中只出现了
6
6
6 个不同字符,其中字符
a
a
a 出现了
45000
45 000
45000 次。

我们有很多方法可以表示这个文件的信息。本节中,考虑一种二进制字符编码方法,每个字符用一个唯一的二进制串表示,称为码字。如果使用定长编码 fixed-length code ,需要用
3
3
3 位表示
6
6
6 个字符:
a
=
000
,
b
=
001
,
…
,
f
=
101
a = 000, b = 001, \dots, f = 101
a=000,b=001,…,f=101 。这种方法需要
300000
300 000
300000 个二进制位来编码文件。是否有更好的编码方案呢?
变长编码 variable-length code 可以达到比定长编码好得多的压缩率,其思想是赋予高频字符短码字、低频字符长码字。图16-3显示了本例的一种变长编码:
1
1
1 位的串
0
0
0 表示
a
a
a ,
4
4
4 位的串
1100
1100
1100 表示
f
f
f 。因此,这种编码表示此文件需要:
(
45
×
1
+
13
×
3
+
12
×
3
+
16
×
3
+
9
×
4
+
5
×
4
)
×
1000
=
224000
位
(45 \times 1 + 13 \times 3 + 12 \times 3 + 16 \times 3 + 9 \times 4 + 5 \times 4) \times 1000 = 224 000位
(45×1+13×3+12×3+16×3+9×4+5×4)×1000=224000位 与定长编码相比节约了
25
%
25\%
25% 的空间。实际上,我们将看到,这是此文件的最优字符编码。
3.1 前缀码
我们这里只考虑所谓前缀码 prefix code(可能无前缀码 prefix-free code 是一个更好的名字,但在相关文献中,前缀码是一致认可的标准术语),即没有任何码字是其他码字的前缀 no codeword is also a prefix of some other codeword 。虽然我们这里不会证明,但与任何字符编码相比,前缀码确实可以保证达到最优数据压缩率,因此我们只关注前缀码,不会丧失一般性。
任何二进制字符码的编码过程都很简单,只要将表示每个字符的码字连接起来、即可完成文件压缩。例如,使用图16-3所示的变长压缩码,可以将 3 3 3 个字符的文件 a b c abc abc 编码为 0 ⋅ 101 ⋅ 100 = 0101100 0 \cdot 101 \cdot 100 = 0101100 0⋅101⋅100=0101100 ,这里用 ⋅ \cdot ⋅ 表示连接操作。
前缀码的作用是简化解码过程。由于没有码字是其他码字的前缀,编码文件的开始码字是无歧义的。我们可以简单地识别出开始码字,将其转换回原字符,然后对编码文件剩余部分重复这种解码过程。在我们的例子中,二进制串
001011101
0010 11101
001011101 可以唯一地解析为
0
⋅
0
⋅
101
⋅
1101
0 \cdot 0 \cdot 101 \cdot 1101
0⋅0⋅101⋅1101 ,解码为
a
a
b
e
aabe
aabe 。
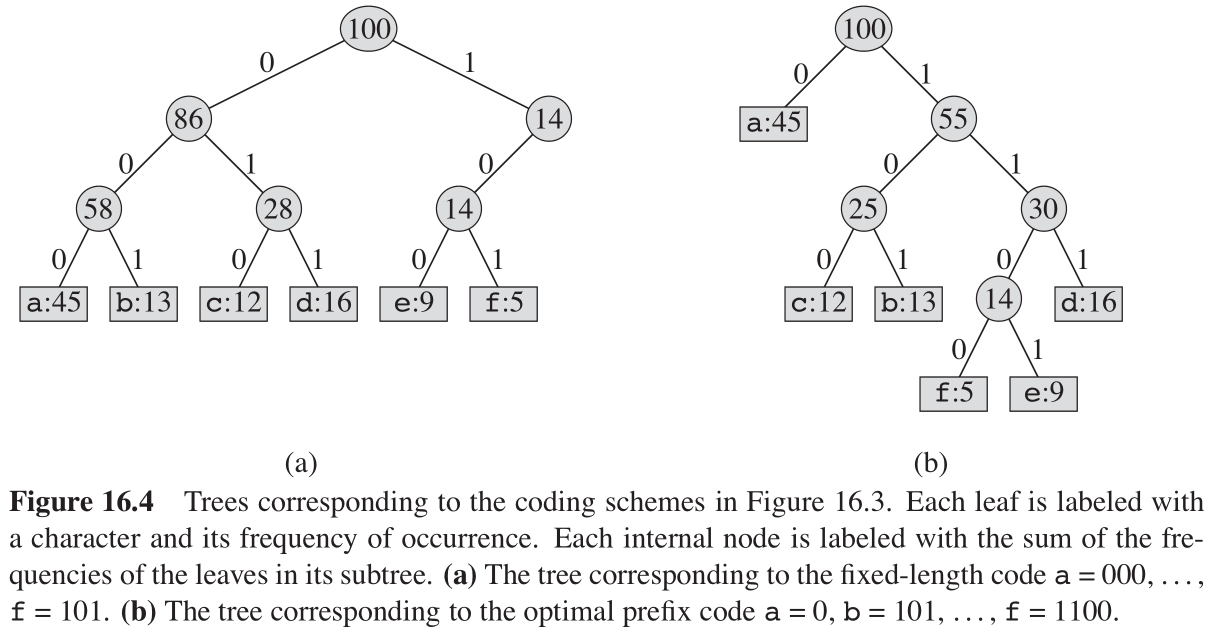
解码过程需要前缀码的一种方便的表示形式,以便我们可以容易地截取开始码字。一种二叉树表示可以满足这种需求,其叶结点为给定的字符。字符的二进制码字用从根结点到该字符叶结点的简单路径表示,其中 0 0 0 意味着“转向左孩子”, 1 1 1 意味着“转向右孩子”。图16-4给出了两个编码示例的二叉树表示。注意,编码树并不是二叉搜索树,因为叶结点并未有序排列,而内部结点并不包含字符关键字。
文件的最优编码方案总是对应一棵“满 full 二叉树”,即每个非叶结点都有两个孩子结点(算导练习16.3-2)。前文给出的定长编码实例不是最优的,因为它的二叉树表示并非“满二叉树”,如图16-4(a)所示:它包含以
10
10
10 开头的码字,但不包含以
11
11
11 开头的码字。现在我们可以只关注“满二叉树”了,因此可以说,若
C
C
C 为字母表、且所有字符的出现频率均为正数,则最优前缀码对应的树恰有
∣
C
∣
|C|
∣C∣ 个叶结点,每个叶结点对应字母表中一个字符,且恰有
∣
C
∣
−
1
|C| - 1
∣C∣−1 个内部结点(算导练习B.5-3)。
给定一棵对应前缀码的树 T T T ,我们可以容易地计算出编码一个文件需要多少个二进制位。对于字母表 C C C 中的每个字符 c c c ,令属性 c . f r e q c.freq c.freq 表示 c c c 在文件中出现的频率,令 d T ( c ) d_T(c) dT(c) 表示 c c c 的叶结点在树中的深度。注意, d T ( c ) d_T(c) dT(c) 也是字符 c c c 的码字的长度。则编码文件需要: B ( T ) = ∑ c ∈ C c . f r e q ⋅ d T ( c ) (16.4) B(T) = \sum_{c\ \in\ C} c.freq \cdot d_T(c) \tag{16.4} B(T)=c ∈ C∑c.freq⋅dT(c)(16.4)
个二进制位,我们将 B ( T ) B(T) B(T) 定义为 T T T 的代价。
3.2 构造哈夫曼编码
哈夫曼设计了一个贪心算法来构造最优前缀码,即哈夫曼编码 Huffman code 。与(算导16.2节中)我们的观察一致,它的正确性证明也依赖于贪心选择性质与最优子结构。接下来,我们并不是先证明这些性质然后再设计算法,而是与之相反。这样做可以帮助我们明确算法是如何做出贪心选择的。
下面给出的伪代码中,我们假定 C C C 是一个 n n n 个字符的集,而其中每个字符 c ∈ C c \in C c∈C 都是一个对象,其属性 c . f r e q c.freq c.freq 给出了字符的出现频率。算法自底向上地构造出对应最优编码的二叉树 T T T 。它从 ∣ C ∣ |C| ∣C∣ 个叶结点开始,执行 ∣ C ∣ − 1 |C| - 1 ∣C∣−1 个“合并”操作创建出最终的二叉树。算法使用一个以属性 f r e q freq freq 为关键字的最小优先队列 Q Q Q ,以识别两个最低频率的对象来将其合并。当合并两个对象时,得到的新对象的频率设置为原来两个对象的频率之和。
HUFFMAN(C)
n = |C|
Q = C
for i = 1 to n - 1
allocate a new node z
z.left = x = EXTRACT-MIN(Q)
z.right = y = EXTRACT-MIN(Q)
z.freq = x.freq + y.freq
INSERT(Q, z)
return EXTRACT-MIN(Q) // return the root of the tree
对前文给出的例子,哈夫曼算法的执行过程如图16-5所示。由于字母表包含 6 6 6 个字母,初始队列大小为 n = 6 n = 6 n=6 ,需要 5 5 5 个合并步骤构造二叉树。最终的二叉树表示最优前缀码。一个字母的码字为「根结点到该字母叶结点的简单路径」上边标签的序列。
- 第 2 2 2 行用 C C C 中字符初始化最小优先队列 Q Q Q 。
- 第 3 ∼ 8 3 \sim 8 3∼8 行的 for 循环,反复从队列中提取两个频率最小的结点 x , y x, y x,y ,将它们合并为一个新结点 z z z 替代它们。 z z z 的频率为 x , y x, y x,y 的频率之和(第 7 7 7 行),结点 z z z 将 x x x 作为其左孩子、将 y y y 作为其右孩子(顺序是任意的,交换左右孩子会生成一个不同的编码,但代价完全一样)。
- 经过
n
−
1
n - 1
n−1 次合并后,第
9
9
9 行返回队列中剩下的唯一结点——编码树的根结点。

如果我们不使用变量 x x x 和 y y y(第 5 , 6 5, 6 5,6 行直接对 z . l e f t , z . r i g h t z.left, z.right z.left,z.right 赋值,将第 7 7 7 行改为 z . f r e q = z . l e f t . f r e q + z . r i g h t . f r e q z.freq = z.left.freq + z.right.freq z.freq=z.left.freq+z.right.freq ),算法还是会生成相同的结果,但后面在证明算法正确性时,我们需要用到结点名 x x x 和 y y y 。因此,保留 x x x 和 y y y 更方便。
为了分析哈夫曼算法的运行时间,我们假定
Q
Q
Q 是使用最小二叉堆实现的(算导第
6
6
6 章)。对于一个
n
n
n 个字符的集
C
C
C ,我们在第
2
2
2 行用 BUILD-MIN-HEAP 过程(算导第6.3节)将
Q
Q
Q 初始化,花费时间为
O
(
n
)
O(n)
O(n) 。第
3
∼
8
3 \sim 8
3∼8 行的 for 循环执行了
n
−
1
n - 1
n−1 次,且每个堆操作需要
O
(
log
n
)
O(\log n)
O(logn) 的时间,所以循环对总时间的贡献为
O
(
n
log
n
)
O(n\log n)
O(nlogn) 。因此,处理一个
n
n
n 个字符的集,HUFFMAN 的总运行时间为
O
(
n
log
n
)
O(n\log n)
O(nlogn) 。如果将最小二叉堆转换为 van Emde Boas 树(算导第20章),我们可以将运行时间减少为
O
(
n
log
log
n
)
O(n\log \log n)
O(nloglogn) 。
3.3 哈夫曼算法的正确性
为了证明贪心算法 HUFFMAN 是正确的,我们证明:确定最优前缀码的问题具有贪心选择和最优子结构性质。下面的引理证明,问题具有贪心选择性质。
引理16.2 令
C
C
C 为一个字母表,其中每个字符
c
∈
C
c \in C
c∈C 都有一个频率
c
.
f
r
e
q
c.freq
c.freq 。令
x
,
y
x, y
x,y 是
C
C
C 中频率最低的两个字符,那么存在
C
C
C 的一个最优前缀码,
x
,
y
x, y
x,y 的码字长度相同,且只有最后一个二进制位不同。
证明:证明的思路是,令
T
T
T 表示任意一个最优前缀码所对应的编码树,对其进行修改,得到表示另外一个最优前缀码的编码树,使得在新树中,
x
x
x 和
y
y
y 是深度最大的叶结点,且它们为兄弟结点。如果可以构造出这样一棵树,那么
x
,
y
x, y
x,y 的码字将有相同长度,且只有最后一位不同。
令 a , b a, b a,b 是 T T T 中深度最大的兄弟叶结点。不失一般性,假定 a . f r e q ≤ b . f r e q a.freq \le b.freq a.freq≤b.freq 且 x . f r e q ≤ y . f r e q x.freq \le y.freq x.freq≤y.freq 。由于 x . f r e q x.freq x.freq 和 y . f r e q y.freq y.freq 是叶结点中最低的两个频率,而 a . f r e q a.freq a.freq 和 b . f r e q b.freq b.freq 是两个任意频率,因此我们有 x . f r e q ≤ a . f r e q x.freq \le a.freq x.freq≤a.freq 且 y . f r e q ≤ b . f r e q y.freq \le b.freq y.freq≤b.freq 。
在证明的剩余部分,有可能 x . f r e q = a . f r e q x.freq = a.freq x.freq=a.freq 或 y . f r e q = b . f r e q y.freq = b.freq y.freq=b.freq 成立。但是如果 x . f r e q = b . f r e q x.freq = b.freq x.freq=b.freq ,则有 a . f r e q = b . f r e q = x . f r e q = y . f r e q a.freq = b.freq = x.freq = y.freq a.freq=b.freq=x.freq=y.freq(算导练习16.3-1),此时引理显然是成立的。因此,我们假定 x . f r e q ≠ b . f r e q x.freq \ne b.freq x.freq=b.freq ,这意味着 x ≠ b x \ne b x=b 。
如图16-6所示,我们在
T
T
T 中交换
x
x
x 和
a
a
a 生成一棵新树
T
′
T'
T′ ,并在
T
′
T'
T′ 中交换
b
b
b 和
y
y
y 生成一棵新树
T
′
′
T''
T′′ ,那么在
T
′
′
T''
T′′ 中
x
,
y
x, y
x,y 是深度最深的两个兄弟叶结点(注意,如果
x
=
b
x = b
x=b 但
y
≠
a
y \ne a
y=a ,那么
T
′
′
T''
T′′ 中
x
x
x 和
y
y
y 不是深度最深的兄弟叶结点)。由公式
(
16.4
)
(16.4)
(16.4) ,
T
T
T 和
T
′
T'
T′ 的代价差为:
B
(
T
)
−
B
(
T
′
)
=
∑
c
∈
C
c
.
f
r
e
q
⋅
d
T
(
c
)
−
∑
c
∈
C
c
.
f
r
e
q
⋅
d
T
′
(
C
)
=
x
.
f
r
e
q
⋅
d
T
(
x
)
+
a
.
f
r
e
q
⋅
d
T
(
a
)
−
x
.
f
r
e
q
⋅
d
T
′
(
x
)
−
a
.
f
r
e
q
⋅
d
T
′
(
a
)
=
x
.
f
r
e
q
⋅
d
T
(
x
)
+
a
.
f
r
e
q
⋅
d
T
(
a
)
−
x
.
f
r
e
q
⋅
d
T
(
a
)
−
a
.
f
r
e
q
⋅
d
T
(
x
)
=
(
a
.
f
r
e
q
−
x
.
f
r
e
q
)
(
d
T
(
a
)
−
d
T
(
x
)
)
≥
0
\begin{aligned}B(T) - B(T') &= \sum_{c\ \in\ C} c.freq \cdot d_T(c) - \sum_{c\ \in \ C} c.freq \cdot d_{T'}(C) \\ &= x.freq \cdot d_T(x) + a.freq \cdot d_T(a) - x.freq \cdot d_{T'} (x) - a.freq \cdot d_{T'}(a) \\ &= x.freq \cdot d_T(x) + a.freq \cdot d_T(a) - x.freq \cdot d_T(a) - a.freq \cdot d_T(x) \\ &= (a.freq - x.freq) (d_T(a) - d_T(x)) \\ &\ge 0\end{aligned}
B(T)−B(T′)=c ∈ C∑c.freq⋅dT(c)−c ∈ C∑c.freq⋅dT′(C)=x.freq⋅dT(x)+a.freq⋅dT(a)−x.freq⋅dT′(x)−a.freq⋅dT′(a)=x.freq⋅dT(x)+a.freq⋅dT(a)−x.freq⋅dT(a)−a.freq⋅dT(x)=(a.freq−x.freq)(dT(a)−dT(x))≥0
因为 a . f r e q − x . f r e q a.freq - x.freq a.freq−x.freq 和 d T ( a ) − d T ( x ) d_T(a) - d_T(x) dT(a)−dT(x) 都是非负的。更具体地, a . f r e q − x . f r e q a.freq - x.freq a.freq−x.freq 是非负的,因为 x x x 是出现频率最低的叶结点; d T ( a ) − d T ( x ) d_T(a) - d_T(x) dT(a)−dT(x) 是非负的,因为 a a a 是 T T T 中深度最深的叶结点。
类似地,交换 y y y 和 b b b 也不能增加代价,所以 B ( T ′ ) − B ( T ′ ′ ) B(T') - B(T'') B(T′)−B(T′′) 也是非负的。因此 B ( T ′ ′ ) ≤ B ( T ) B(T'') \le B(T) B(T′′)≤B(T) ,由于 T T T 是最优的,我们有 B ( T ) ≤ B ( T ′ ′ ) B(T) \le B(T'') B(T)≤B(T′′) ,这意味着 B ( T ′ ′ ) = B ( T ) B(T'') = B(T) B(T′′)=B(T) 。因此, T ′ ′ T'' T′′ 也是最优树,且 x x x 和 y y y 是其中深度最深的兄弟叶结点,引理成立。 ■ \blacksquare ■
引理16.2说明,不失一般性,通过合并来构造最优树的过程,可以从合并出现频率最低的两个字符这样一个贪心选择开始。为什么这是一个贪心选择?我们可以将一次合并操作的代价、看作是被合并的两项的频率之和。(算导练习16.3-4要求)证明,构造编码树的总代价等于所有合并操作的代价之和。在每一步可选的所有合并操作中,HUFFMAN 选择的是代价最小的那个。
下面的引理证明了,构造最优前缀码的问题具有最优子结构性质。
引理16.3 令
C
C
C 为一个给定的字母表,其中每个字符
x
∈
C
x \in C
x∈C 都定义了一个频率
c
.
f
r
e
q
c.freq
c.freq 。令
x
x
x 和
y
y
y 是
C
C
C 中频率最低的两个字符。令
C
′
C'
C′ 为
C
C
C 去掉字符
x
x
x 和
y
y
y 、加入一个新字符
z
z
z 后得到的字母表,即
C
′
=
C
−
{
x
,
y
}
∪
{
z
}
C' = C - \{ x, y \} \cup \{ z\}
C′=C−{x,y}∪{z} 。类似
C
C
C ,也为
C
′
C'
C′ 定义
f
r
e
q
freq
freq ,不同之处只是
z
.
f
r
e
q
=
x
.
f
r
e
q
+
y
.
f
r
e
q
z.freq = x.freq + y.freq
z.freq=x.freq+y.freq 。令
T
′
T'
T′ 为字母表
C
′
C'
C′ 的任意一个最优前缀码对应的编码树。于是我们可以将
T
′
T'
T′ 中叶结点
z
z
z 替换为一个以
x
x
x 和
y
y
y 为孩子的内部结点,得到树
T
T
T ,而
T
T
T 表示字母表
C
C
C 的一个最优前缀码(看不太懂?是说贪心选择+子问题最优解=原问题最优解?)。
证明:首先说明如何用树
T
′
T'
T′ 的代价
B
(
T
′
)
B(T')
B(T′) 来表示树
T
T
T 的代价
B
(
T
)
B(T)
B(T) ,方法是考虑公式
(
16.4
)
(16.4)
(16.4) 中每项的代价。对于每个字符
c
∈
C
−
{
x
,
y
}
c \in C - \{ x, y\}
c∈C−{x,y} ,我们有
d
T
(
c
)
=
d
T
′
(
c
)
d_T(c) = d_{T'} (c)
dT(c)=dT′(c) ,因此
c
.
f
r
e
q
⋅
d
T
(
c
)
=
c
.
f
r
e
q
⋅
d
T
′
(
c
)
c.freq \cdot d_T(c) = c.freq \cdot d_{T'} (c)
c.freq⋅dT(c)=c.freq⋅dT′(c) 。由于
d
T
(
x
)
=
d
T
(
y
)
=
d
T
′
(
z
)
+
1
d_T(x) = d_T(y) = d_{T'} (z ) + 1
dT(x)=dT(y)=dT′(z)+1 ,我们有:
x
.
f
r
e
q
⋅
d
T
(
x
)
+
y
.
f
r
e
q
⋅
d
T
(
y
)
=
(
x
.
f
r
e
q
+
y
.
f
r
e
q
)
(
d
T
′
(
z
)
+
1
)
=
z
.
f
r
e
q
⋅
d
T
′
(
z
)
+
(
x
.
f
r
e
q
+
y
.
f
r
e
q
)
x.freq \cdot d_T(x) +y.freq \cdot d_T(y) = (x.freq + y.freq) (d_{T'} (z) + 1) \\ = z.freq \cdot d_{T'} (z) + (x.freq + y.freq)
x.freq⋅dT(x)+y.freq⋅dT(y)=(x.freq+y.freq)(dT′(z)+1)=z.freq⋅dT′(z)+(x.freq+y.freq)
于是可以得到结论: B ( T ) = B ( T ′ ) + x . f r e q + y . f r e q B(T)= B(T') + x.freq + y.freq B(T)=B(T′)+x.freq+y.freq
或者等价地: B ( T ′ ) = B ( T ) − x . f r e q − y . f r e q B(T') = B(T) - x.freq - y.freq B(T′)=B(T)−x.freq−y.freq
现在用反证法来证明引理。假定
T
T
T 对应的前缀码并不是
C
C
C 的最优前缀码。存在最优编码树
T
′
′
T''
T′′ 满足
B
(
T
′
′
)
<
B
(
T
)
B(T'') < B(T)
B(T′′)<B(T) 。不失一般性(由引理16.2),
T
′
′
T''
T′′ 包含兄弟结点
x
x
x 和
y
y
y 。令
T
′
′
′
T'''
T′′′ 为将
T
′
′
T''
T′′ 中
x
,
y
x, y
x,y 及它们的父结点替换为叶结点
z
z
z 得到的树,其中
z
.
f
r
e
q
=
x
.
f
r
e
q
+
y
.
f
r
e
q
z.freq = x.freq + y.freq
z.freq=x.freq+y.freq 。于是:
B
(
T
′
′
′
)
=
B
(
T
′
′
)
−
x
.
f
r
e
q
−
y
.
f
r
e
q
<
B
(
T
)
−
x
.
f
r
e
q
−
y
.
f
r
e
q
=
B
(
T
′
)
B(T''') = B(T'') - x.freq - y.freq < B(T)- x.freq - y.freq = B(T')
B(T′′′)=B(T′′)−x.freq−y.freq<B(T)−x.freq−y.freq=B(T′)
与 T ′ T' T′ 对应 C ′ C' C′ 的一个最优前缀码的假设矛盾。因此, T T T 必然表示字母表 C C C 的一个最优前缀码。 ■ \blacksquare ■
定理16.4 过程 HUFFMAN 会生成一个最优前缀码。
证明:由引理16.2和引理16.3即可得。
■
\blacksquare
■
4. 拟阵和贪心算法
这里概略介绍一种与贪心算法相关的漂亮的理论。该理论描述了很多贪心方法生成最优解的情形。它涉及一种称为“拟阵”的组合结构。虽然这种理论不能涵盖贪心方法适用的所有情况(例如,它不能用于活动选择问题和哈夫曼编码问题),但它确实覆盖了很多有实际意义的情况。而且这种理论的扩展,还覆盖了其他很多应用(算导第16章注记)。
4.1 拟阵
一个拟阵 matroid 就是一个满足如下条件的序偶
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) :
- S S S 是一个有限集。
-
ℓ
ℓ
ℓ 是
S
S
S 的子集的一个非空族
a nonempty family of subsets of S,(这些子集)称为 S S S 的独立子集independent subsets,使得如果 B ∈ ℓ B \in ℓ B∈ℓ 且 A ⊆ B A \subseteq B A⊆B ,则 A ∈ ℓ A \in ℓ A∈ℓ 。如果 ℓ ℓ ℓ 满足此性质,我们称 ℓ ℓ ℓ 是遗传的hereditary。注意,空集 ∅ \varnothing ∅ 必然是 ℓ ℓ ℓ 的成员。 - 如
A
∈
ℓ
,
B
∈
ℓ
A \in ℓ, B \in ℓ
A∈ℓ,B∈ℓ 且
∣
A
∣
<
∣
B
∣
|A| < |B|
∣A∣<∣B∣ ,那么存在某个元素
x
∈
B
−
A
x \in B - A
x∈B−A ,使得
A
∪
{
x
}
∈
ℓ
A \cup \{ x \} \in ℓ
A∪{x}∈ℓ ,则称
M
M
M 满足交换性质
exchange property。
“拟阵”一词最早是 Hassler Whitney 提出的。他当时在研究矩阵拟阵 matric matroid ,其中
S
S
S 的元素是一个给定矩阵的所有行,而行之间的独立性质与通常意义上的线性无关性质是等价的 a set of rows is independent if they are linearly independent in the usual sense 。(算导练习16.4-2要求)证明,这个结构定义了一个拟阵。
另一个拟阵的例子是图拟阵 graphic matroid
M
G
=
(
S
G
,
ℓ
G
)
M_G = (S_G, ℓ_G)
MG=(SG,ℓG) ,它定义在一个给定的无向图
G
=
(
V
,
E
)
G=(V, E)
G=(V,E) 之上:
- S G S_G SG 定义为 E E E ,即 G G G 的边集。
- 如果 A A A 是 E E E 的子集,则 A ∈ ℓ G A \in ℓ_G A∈ℓG 当且仅当 A A A 是无圈的。也就是说,一组边 A A A 是独立的当且仅当子图 G A = ( V , A ) G_A = (V, A) GA=(V,A) 形成一个森林。
图拟阵 M G M_G MG 与最小生成树问题是紧密相关的(算导第23章可能讨论)。
定理16.5 如果
G
=
(
V
,
E
)
G = (V, E)
G=(V,E) 是一个无向图,则
M
G
=
(
S
G
,
ℓ
G
)
M_G = (S_G, ℓ_G)
MG=(SG,ℓG) 是一个拟阵。
证明:显然
S
G
=
E
S_G = E
SG=E 是一个有限集。而且,
ℓ
G
ℓ_G
ℓG 是遗传的,因为森林的子集还是森林。换句话说,从一个无圈的边集中删除边不会产生圈 removing edges from an acyclic set of edges cannot create cycles 。
因此,接下来只需证明 M G M_G MG 满足交换性质。假定 G A = ( V , A ) G_A = (V, A) GA=(V,A) 和 G B = ( V , B ) G_B = (V, B) GB=(V,B) 是 G G G 的森林,且 ∣ B ∣ > ∣ A ∣ |B| > |A| ∣B∣>∣A∣ 。也就是说, A A A 和 B B B 是无圈边集,且 B B B 包含更多的边。
我们有结论:
F
=
(
V
F
,
E
F
)
F= (V_F, E_F)
F=(VF,EF) 恰好包含
∣
V
F
∣
−
∣
E
F
∣
| V_F | - |E_F|
∣VF∣−∣EF∣ 棵树。为了证明此结论,假定
F
F
F 包含
t
t
t 棵树,其中第
i
i
i 棵树包含
v
i
v_i
vi 个顶点和
e
i
e_i
ei 条边。于是有:
∣
E
F
∣
=
∑
i
=
1
t
e
i
=
∑
i
=
1
t
(
v
i
−
1
)
由
定
理
B
.
2
=
∑
i
=
1
t
v
i
−
t
=
∣
V
F
∣
−
t
\begin{aligned} |E_F| &= \sum^t_{i=1} e_i = \sum^t_{i=1} (v_i - 1) \quad 由定理B.2 \\ &= \sum^t_{i=1} v_i - t = |V_F |- t \end{aligned}
∣EF∣=i=1∑tei=i=1∑t(vi−1)由定理B.2=i=1∑tvi−t=∣VF∣−t 这意味着
t
=
∣
V
F
∣
−
∣
E
F
∣
t = |V_F | - |E_F|
t=∣VF∣−∣EF∣ 。因此,森林
G
A
G_A
GA 包含
∣
V
∣
−
∣
A
∣
|V| - |A|
∣V∣−∣A∣ 棵树,森林
G
B
G_B
GB 包含
∣
V
∣
−
∣
B
∣
|V| - |B|
∣V∣−∣B∣ 棵树。
由于森林 G B G_B GB 中树的数量比森林 G A G_A GA 少,它必然包含某棵树 T T T ,其顶点在森林 G A G_A GA 中属于两棵不同的树。而且,由于 T T T 是连通的,它必然包含一条边 ( u , v ) (u, v) (u,v) ,使得顶点 u u u 和 v v v 在森林 G A G_A GA 中属于两棵不同的树。由于边 ( u , v ) (u, v) (u,v) 连接了森林 G A G_A GA 中两棵不同的树中的顶点,可以将边 ( u , v ) (u, v) (u,v) 加入森林 G A G_A GA ,而不会产生圈。因此, M G M_G MG 满足交换性质。至此,已证明 M G M_G MG 是拟阵。 ■ \blacksquare ■
给定一个拟阵
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) ,如果对一个集
A
∈
ℓ
A \in ℓ
A∈ℓ 和一个元素
x
∉
A
x \notin A
x∈/A ,将
x
x
x 加入
A
A
A 且保持独立性质,则称
x
x
x 是
A
A
A 的一个扩展 extension 。也就是说,如果
A
∪
{
x
}
∈
ℓ
A \cup \{ x\} \in ℓ
A∪{x}∈ℓ ,则
x
x
x 是
A
A
A 的一个扩展。我们以图拟阵
M
G
M_G
MG 为例,如果
A
A
A 是一个独立的边集,那么边
e
e
e 是
A
A
A 的一个扩展、当且仅当
e
e
e 不在
A
A
A 中且将
e
e
e 加入
A
A
A 中不会形成圈。
对拟阵
M
M
M 中的一个独立子集
A
A
A ,如果它不存在扩展,则称它是最大的 maximal 。也就是说,如果
A
A
A 不包含于任何更大的
M
M
M 的独立子集中,则
A
A
A 是最大的。下面的性质通常很有用。
定理16.6 拟阵中所有最大独立子集都具有相同大小。
证明:假定命题不成立,拟阵
M
M
M 存在一个最大独立子集
A
A
A 和另一个更大的独立子集
B
B
B 。那么,交换性质意味着对于某个
x
∈
B
−
A
x \in B - A
x∈B−A ,我们可以将
A
A
A 扩展为一个更大的独立子集
A
∪
{
x
}
A \cup \{ x\}
A∪{x} ,与
A
A
A 是最大独立子集的假设矛盾。
■
\blacksquare
■
作为此定理的一个示例,我们考虑一个连通无向图
G
G
G 的图拟阵
M
G
M_G
MG 。
M
G
M_G
MG 的每个最大独立子集必定是一棵边数为
∣
V
∣
−
1
|V| - 1
∣V∣−1 、连接了
G
G
G 的所有顶点的自由树 free tree ,这样一棵树称为
G
G
G 的生成树 spanning tree 。
如果一个拟阵
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) 关联一个权重函数
w
w
w ,为每个元素
x
∈
S
x \in S
x∈S 赋予一个严格大于
0
0
0 的权重
w
(
x
)
w(x)
w(x) ,则称
M
M
M 是加权的 weighted 。通过求和,可将权重函数
w
w
w 扩展到
S
S
S 的任意子集
A
A
A :
w
(
A
)
=
∑
x
∈
A
w
(
x
)
w(A) = \sum_{x \in A} w(x)
w(A)=x∈A∑w(x)
例如,如果令 w ( e ) w(e) w(e) 表示图拟阵 M G M_G MG 中边 e e e 的权重,那么 w ( A ) w(A) w(A) 就表示边集 A A A 中所有边的权重之和。
4.2 加权拟阵上的贪心算法
很多可以用贪心算法得到最优解的问题,都可以形式化为「在一个加权拟阵中寻找最大权重独立子集」的问题。也就是说,给定一个加权拟阵 M = ( S , ℓ ) M = (S, ℓ) M=(S,ℓ) ,我们希望寻找独立集 A ∈ ℓ A \in ℓ A∈ℓ 、使得 w ( A ) w(A) w(A) 最大。我们称这种「独立且具有最大可能权重的子集」为拟阵的最优子集。由于任何元素 x ∈ S x \in S x∈S 的权重 w ( x ) w(x) w(x) 都是正的,则最优子集必然是最大独立子集——它总是有助于使 A A A 尽可能大。
例如,在最小生成树问题中,给定一个连通无向图
G
=
(
V
,
E
)
G = (V, E)
G=(V,E) 和一个长度函数
w
w
w ,使得
w
(
e
)
w(e)
w(e) 表示边
e
e
e 的长度(正值)(这里我们用“长度”表示图中边的原始权重,用“权重”表示关联的拟阵的权重)。我们希望找到一个边的子集,能连接所有顶点,且具有最小总长度。为了将此问题描述为「寻找拟阵最优子集」的问题,考虑加权拟阵
M
G
M_G
MG ,其权重函数为
w
′
w'
w′ ,这里
w
′
(
e
)
=
w
0
−
w
(
e
)
w'(e) = w_0 - w(e)
w′(e)=w0−w(e) ,其中
w
0
w_0
w0 为大于最大边长度的值。在此加权拟阵中,所有权重均为正,且最优子集即为原图中的最小总长度生成树。更具体地,每个最大独立子集
A
A
A 都对应一棵
∣
V
∣
−
1
|V| - 1
∣V∣−1 条边的生成树,而且由于对所有最大独立子集
A
A
A ,有:
w
′
(
A
)
=
∑
e
∈
A
w
′
(
e
)
=
∑
e
∈
A
(
w
0
−
w
(
e
)
)
=
(
∣
V
∣
−
1
)
w
0
−
∑
e
∈
A
w
(
e
)
=
(
∣
V
∣
−
1
)
w
0
−
w
(
A
)
w'(A) = \sum_{e \in A} w'(e) = \sum_{e \in A} (w_0 - w(e)) = ( | V| - 1) w_0 - \sum_{e \in A}w(e) = (|V| - 1) w_0 - w(A)
w′(A)=e∈A∑w′(e)=e∈A∑(w0−w(e))=(∣V∣−1)w0−e∈A∑w(e)=(∣V∣−1)w0−w(A) 因此,最大化
w
′
(
A
)
w'(A)
w′(A) 必然最小化
w
(
A
)
w(A)
w(A) 。因此,任何能求得任意拟阵中最优子集
A
A
A 的算法,均可求解最小生成树问题。
(算导第23章给出最小生成树的算法)但现在我们给出适用于任何加权拟阵的算法。算法接受一个加权拟阵 M = ( S , ℓ ) M = (S, ℓ) M=(S,ℓ) 及其关联的正加权函数 w w w 作为输入,返回最优子集 A A A 。在我们的伪码中,用 M . S M.S M.S 和 M . ℓ M.ℓ M.ℓ 表示 M M M 的组成部分,加权函数表示为 w w w 。这个算法是一个贪心算法,因为它按权重单调递减的顺序、考虑每个元素 x ∈ S x \in S x∈S ,如果 A ∪ { x } A \cup \{ x\} A∪{x} 是独立的,就立即将 x x x 加入到累积集 A A A 中。
GREEDY(M, w)
A = ∅
sort M.S into monotonically decreasing order by weight w
for each x in M.S, taken in monotonically decreasing order by weight w(x)
if A ∪ {x} in M.ℓ
A = A ∪ {x}
return A
第四行检查加入
x
x
x 后
A
A
A 是否保持独立集性质,若是则在第五行将
x
x
x 加入
A
A
A ,否则丢弃
x
x
x 。由于空集是独立的,且每步 for 循环都保持
A
A
A 的独立性,因此由归纳法可知,
A
A
A 始终是独立的。因此,GREEDY 总是返回一个独立子集
A
A
A 。稍后,我们会看到
A
A
A 是具有最大可能权重的子集,因而是一个最优子集。
GREEDY 的运行时间很容易分析。令
n
n
n 表示
∣
S
∣
|S|
∣S∣ ,则排序阶段花费时间为
O
(
n
log
n
)
O(n\log n)
O(nlogn) 。第四行严格执行了
n
n
n 次,每次处理
S
S
S 的一个元素。第四行每执行一次需要检查一个集
A
∪
{
x
}
A\cup \{x\}
A∪{x} 是否独立。如果每次检查花费时间为
O
(
f
(
n
)
)
O(f(n))
O(f(n)) ,则算法运行时间为
O
(
n
log
n
+
n
f
(
n
)
)
O(n\log n + n f(n))
O(nlogn+nf(n)) 。
现在证明 GREEDY 返回一个最优子集。
引理16.7(拟阵具有贪心选择性质 Matroids exhibit the greedy-choice property )假定
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) 是一个加权拟阵,加权函数为
w
w
w ,且
S
S
S 已按权重单调递减顺序排序。令
x
x
x 是
S
S
S 中第一个满足
{
x
}
\{ x\}
{x} 独立的元素(如果存在)。如果存在这样的
x
x
x ,那么存在
S
S
S 的一个最优子集
A
A
A 包含
x
x
x 。
证明:如果不存在这样的
x
x
x ,唯一的独立子集是空集,显然引理成立。否则,令
B
B
B 为任意非空最优子集。假定
x
∉
B
x \notin B
x∈/B ,因为否则的话,显然
B
B
B 就是我们要找的包含
x
x
x 的最优子集
A
A
A 。
我们有结论, B B B 中元素的权重都不大于 w ( x ) w(x) w(x) 。原因在于,我们观察到 y ∈ B y \in B y∈B 意味着 { y } \{ y \} {y} 是独立的(因为 B ∈ ℓ B \in ℓ B∈ℓ 且 ℓ ℓ ℓ 是遗传的),因此我们选择 x x x 的方式(第一个形成独立集的元素)保证了对任意 y ∈ B y \in B y∈B ,有 w ( x ) ≥ w ( y ) w(x) \ge w(y) w(x)≥w(y) 。
于是可以这样构造集 A A A 。以 A = { x } A = \{ x\} A={x} 开始,由于 x x x 的性质,集 A A A 保证是独立的。使用交换性质,反复寻找 B B B 中一个可以加入 A A A 中的新元素(同时保持 A A A 的独立性),直到 ∣ A ∣ = ∣ B ∣ |A| = |B| ∣A∣=∣B∣ 。此时, A A A 和 ∣ B ∣ |B| ∣B∣ 的差别仅在于 A A A 包含 x x x 、而 B B B 包含另一个元素 y y y 。也就是说, A = B − { y } ∪ { x } A = B - \{ y \} \cup \{ x \} A=B−{y}∪{x} , y y y 为 B B B 中某个元素,且: w ( A ) = w ( B ) − w ( y ) + w ( x ) ≥ w ( B ) w(A) = w(B) - w(y) + w(x) \ge w(B) w(A)=w(B)−w(y)+w(x)≥w(B)
由于集 B B B 是最优的,因此集 A A A 必然也是最优的,且包含 x x x 。 ■ \blacksquare ■
下面证明,如果一个元素在初始时不是最优的选择,那么在随后也不会被选入最优集中。
引理16.8 令
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) 是一个拟阵。如果
x
x
x 是
S
S
S 中一个元素,而且是
S
S
S 的某个独立子集
A
A
A 的一个扩展,则
x
x
x 也是
∅
\varnothing
∅ 的一个扩展。
证明:由于
x
x
x 是
A
A
A 的一个扩展,可知
A
∪
{
x
}
A\cup \{ x\}
A∪{x} 是独立的。由于
ℓ
ℓ
ℓ 是遗传的,
{
x
}
\{ x\}
{x} 必然是独立的。因此,
x
x
x 是
∅
\varnothing
∅ 的一个扩展。
■
\blacksquare
■
推论16.9 令
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) 是一个拟阵。如果
x
x
x 是
S
S
S 中一个元素,且它不是
∅
\varnothing
∅ 的一个扩展,那么它也不是
S
S
S 的任何独立子集
A
A
A 的扩展。
证明:此推论为引理16.8的逆否命题。
■
\blacksquare
■
推论16.9表明,任何元素如果首次不能用于构造独立集,则之后永远也不可能被用到了。因此,GREEDY 跳过
S
S
S 中那些不是
∅
\varnothing
∅ 的扩展的初始元素,不会导致错误结果,因为那些元素永远不会被用到。
引理16.10(拟阵具有最优子结构性质 Matroids exhibit the optimal-substructure property )令
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) 是一个加权拟阵,
x
x
x 是
S
S
S 中第一个被 GREEDY 算法选出的元素,则接下来寻找一个包含
x
x
x 的最大权重独立子集的问题,归结为寻找加权拟阵
M
′
=
(
S
′
,
ℓ
′
)
M' = (S', ℓ')
M′=(S′,ℓ′) 的一个最大权重独立子集的问题,其中:
S
′
=
{
y
∈
S
∣
{
x
,
y
}
∈
ℓ
}
ℓ
′
=
{
B
⊆
S
−
{
x
}
∣
B
∪
{
x
}
∈
ℓ
}
\begin{aligned} S' &= \{ y \in S \mid \{ x , y \} \in ℓ\} \\ ℓ' &= \{ B \subseteq S - \{ x \} \mid B \cup \{ x\} \in ℓ\}\end{aligned}
S′ℓ′={y∈S∣{x,y}∈ℓ}={B⊆S−{x}∣B∪{x}∈ℓ}
M
′
M'
M′ 的权重函数就是
M
M
M 的权重函数,但只局限于
S
′
S'
S′ 中元素(我们称
M
′
M'
M′ 为
M
M
M 在元素
x
x
x 上的收缩 contraction )。
证明:若
A
A
A 是
M
M
M 的任意一个包含
x
x
x 的最大权重独立子集,则
A
′
=
A
−
{
x
}
A' = A - \{ x \}
A′=A−{x} 是
M
′
M'
M′ 的一个独立子集。相反,任何
M
′
M'
M′ 的独立子集
A
′
A'
A′ 可生成
M
M
M 的独立子集
A
=
A
′
∪
{
x
}
A = A' \cup \{ x \}
A=A′∪{x} 。由于对两种情况均有
w
(
A
)
=
w
(
A
′
)
+
w
(
x
)
w(A) = w(A') + w(x)
w(A)=w(A′)+w(x) ,因此
M
M
M 的包含
x
x
x 的最大权重独立子集、必然生成
M
′
M'
M′ 的最大权重独立子集,反之亦然(?)。
■
\blacksquare
■
定理16.11(拟阵上贪心算法的正确性)若
M
=
(
S
,
ℓ
)
M = (S, ℓ)
M=(S,ℓ) 是一个加权拟阵,权重函数是
w
w
w ,那么 GREEDY(M, w) 返回一个最优子集。
证明:由推论16.9,GREEDY 跳过的任何不是
∅
\varnothing
∅ 的扩展的初始元素可永远丢弃,因为这些元素永远不会被用到。一旦 GREEDY 算法选出第一个元素
x
x
x ,引理16.7表明算法将
x
x
x 加入
A
A
A 不会导致错误结果,因为必然存在包含
x
x
x 的最优子集。最终,引理16.10说明,剩下的问题就是如何寻找拟阵
M
′
M'
M′ 的最优子集了,
M
′
M'
M′ 是
M
M
M 在
x
x
x 上的收缩。在 GREEDY 将
A
A
A 设置为
{
x
}
\{ x\}
{x} 后,我们可以将之后它的所有步骤解释为拟阵
M
′
=
(
S
′
,
ℓ
′
)
M' = (S', ℓ')
M′=(S′,ℓ′) 上的操作,因为对所有集
B
∈
ℓ
′
B \in ℓ'
B∈ℓ′ ,
B
B
B 在
M
′
M'
M′ 中独立当且仅当
B
∪
{
x
}
B \cup \{ x\}
B∪{x} 在
M
M
M 中独立。因此,GREEDY 随后的操作将会找到
M
′
M'
M′ 的一个最大权重独立子集,而其所有操作的总体效果就是找到
M
M
M 的一个最大权重独立子集。
■
\blacksquare
■
5. 用拟阵求解任务调度问题
一个可以用拟阵来求解的问题,是单处理器上的单位时间任务最优调度问题 optimally scheduling unit-time tasks on a single processor ,其中每个任务有一个截止时间、以及错过截止时间后的惩罚值。问题看起来很复杂,但我们可以用一个异常简单的方法求解它——将其转换为一个拟阵、并用贪心算法求解。
单位时间任务是严格需要一个时间单位来完成的作业,如运行在计算机上的一个程序。给定一个单位时间任务的有限集 S S S ,对 S S S 的一个调度是指 S S S 的一个排列,它指明了任务执行的顺序。第一个被调度的任务开始于时刻 0 0 0 ,终止于时刻 1 1 1 ;第二个任务开始于时刻 1 1 1 ,终止于时刻 2 2 2 ;以此类推。单处理器上带截止时间和惩罚的单位时间任务调度问题有如下输入:
- n n n 个单位时间任务的集合 S = { a 1 , a 2 , … , a n } S = \{ a_1, a_2, \dots, a_n\} S={a1,a2,…,an} 。
- n n n 个整数截止时间 d 1 , d 2 , … , d n d_1, d_2, \dots, d_n d1,d2,…,dn ,每个 d i d_i di 满足 1 ≤ d i ≤ n 1 \le d_i \le n 1≤di≤n ,我们期望任务 a i a_i ai 在时间 d i d_i di 之前完成。
- n n n 个非负权重或惩罚 w 1 , w 2 , … , w n w_1, w_2, \dots, w_n w1,w2,…,wn ,若任务 a i a_i ai 在时间 d i d_i di 之前没有完成,我们就会受到 w i w_i wi 这么多的惩罚,如果任务在截止时间前完成,则不会受到惩罚。
我们希望找到
S
S
S 的一个调度方案,能最小化超过截止时间导致的惩罚总和。考虑一个给定的调度方案,如果方案中一个任务在截止时间后完成,我们称它是延迟的 late ;否则我们称它是提前的 early 。对于任意调度方案,我们总是可以将其转换为提前优先形式 early-first form ,即将提前的任务都置于延迟的任务之前。原因在于,如果某个提前任务
a
i
a_i
ai 位于某个延迟任务
a
j
a_j
aj 之后,我们可以交换它们的位置,显然
a
i
a_i
ai 仍然是提前的,
a
j
a_j
aj 仍然是延迟的。
而且,我们总是可以将一个任意的调度方案转换为规范形式 canonical form ——提前任务都在延迟任务之前,且提前任务按截止时间单调递增的顺序排列。为了进行这种转换,我们首先将调度方案转换为提前优先形式。然后只要调度方案中存在两个提前任务
a
i
a_i
ai 和
a
j
a_j
aj ,分别在时刻
k
k
k 和
k
+
1
k+1
k+1 完成,使得
d
j
<
d
i
d_j < d_i
dj<di ,我们就交换
a
i
a_i
ai 和
a
j
a_j
aj 的位置。由于交换前
a
j
a_j
aj 是提前的,我们有
k
+
1
≤
d
j
k + 1 \le d_j
k+1≤dj ,因此
k
+
1
<
d
i
k +1 < d_i
k+1<di ,因而交换后
a
i
a_i
ai 是提前的。由于
a
j
a_j
aj 被移动到更靠前的时间,因此在交换后它保持提前。
这样,寻找最优调度方案的问题,就归结为在最优调度下寻找提前任务集合 A A A 的问题。确定 A A A 之后,我们可以将 A A A 中元素按截止时间递增的顺序排列,然后将延迟任务(即 S − A S - A S−A )以任意顺序排列其后,就得到了最优调度方案的规范形式。
我们称一个任务集合 A A A 是独立的,如果存在一个调度方案使 A A A 中所有任务都不延迟。显然,一个调度方案的提前任务集合构成了一个独立的任务集合。令 I I I 表示所有独立任务集的集合。下面考虑如何确定一个给定集合 A A A 是否独立的问题。对 t = 0 , 1 , 2 , … , n t = 0, 1, 2, \dots, n t=0,1,2,…,n ,令 N t ( A ) N_t(A) Nt(A) 表示 A A A 中截止时间小于等于 t t t 的任务数。注意,对任意集合 A A A 均有 N 0 ( A ) = 0 N_0(A) = 0 N0(A)=0 。
引理16.12 对任意任务集合 A A A ,下面的性质是等价的:
- A A A 是独立的。
- 对 t = 0 , 1 , 2 , … , n t = 0, 1, 2, \dots, n t=0,1,2,…,n ,有 N t ( A ) ≤ t N_t(A) \le t Nt(A)≤t 。
- 如果 A A A 中任务按截止时间单调递增的顺序调度,则没有任务是延迟的。
证明: 为了证明由(1)可得(2),我们证明逆否命题:如果对某个 t t t , N t ( A ) > t N_t(A) > t Nt(A)>t ,则集合 A A A 的任何调度方案都会有任务延迟的情况发生,因为超过 t t t 个任务必须在时刻 t t t 前完成(而每个任务都花费一个时间单位)。因此,由(1)可得(2)。如果(2)成立,则(3)必然也成立:当按截止时间单调递增顺序调度任务时,不会发生“卡住”的现象,因为(2)成立意味着第 i i i 大的截止时间至少是 i i i 。最后,由(3)显然能推导出(1)。 ■ \blacksquare ■
利用引理16.12的性质2,我们可以简单计算出一个给定任务集合是否独立(算导练习16.5-2)。最小化延迟任务的惩罚之和的问题,与最大化提前任务的惩罚之和是等价的。下面的定理确保,我们可以使用贪心算法、求出总惩罚最大的独立任务集 A A A 。
定理16.13 如果
S
S
S 是一个给定了截止时间的单位时间任务集合,
I
I
I 是所有独立任务集合的集合,则对应的系统
(
S
,
I
)
(S, I)
(S,I) 是一个拟阵。
证明:每个独立任务集合的子集必然也是独立的。为了证明交换性质,假定
B
B
B 和
A
A
A 是独立任务集合,且
∣
B
∣
>
∣
A
∣
|B|> |A|
∣B∣>∣A∣ 。令
k
k
k 是满足
N
t
(
B
)
≤
N
t
(
A
)
N_t(B) \le N_t(A)
Nt(B)≤Nt(A) 的最大的
t
t
t(这样的
t
t
t 肯定存在,因为
N
0
(
A
)
=
N
0
(
B
)
=
0
N_0(A) = N_0(B) = 0
N0(A)=N0(B)=0 )。由于
N
n
(
B
)
=
∣
B
∣
N_n(B) = |B|
Nn(B)=∣B∣ 且
N
n
(
A
)
=
∣
A
∣
N_n(A) = |A|
Nn(A)=∣A∣ ,但
∣
B
∣
>
∣
A
∣
|B| > |A|
∣B∣>∣A∣ ,因此对
k
+
1
≤
j
≤
n
k + 1\le j \le n
k+1≤j≤n 间的所有
j
j
j ,必然有
k
<
n
k < n
k<n 以及
N
j
(
B
)
>
N
j
(
A
)
N_j(B)> N_j(A)
Nj(B)>Nj(A) 。因此,
B
B
B 比
A
A
A 包含更多截止时间为
k
+
1
k +1
k+1 的任务。令
a
i
a_i
ai 为
B
−
A
B - A
B−A 中截止时间为
k
+
1
k +1
k+1 的任务,令
A
′
=
A
∪
{
a
i
}
A' = A\cup \{ a_i \}
A′=A∪{ai} 。
下面利用引理16.12的性质2,证明 A ′ A' A′ 必然是独立的。因为 A A A 是独立的,对 0 ≤ t ≤ k 0 \le t \le k 0≤t≤k ,我们有 N t ( A ′ ) = N t ( A ) ≤ t N_t(A') = N_t(A) \le t Nt(A′)=Nt(A)≤t 。因为 B B B 是独立的,对 k < t ≤ n k < t \le n k<t≤n ,我们有 N t ( A ′ ) ≤ N t ( B ) ≤ t N_t(A') \le N_t(B) \le t Nt(A′)≤Nt(B)≤t 。因此, A ′ A' A′ 是独立的,从而得证 ( S , I ) (S, I) (S,I) 是一个拟阵。 ■ \blacksquare ■
由定理16.11,我们可以用贪心算法求出一个最大权重的独立任务集
A
A
A 。然后可以创建一个最优调度方案,以
A
A
A 中任务为提前任务。这个算法是求解单处理器上带截止时间和惩罚的单位时间任务调度问题的一种高效算法。使用 GREEDY 的运行时间为
O
(
n
2
)
O(n^2)
O(n2) ,因为算法共进行了
O
(
n
)
O(n)
O(n) 独立性检查,每次花费
O
(
n
)
O(n)
O(n) 时间(算导练习16.5-2)。(算导思考题16-4)给出了一个更快的实现。

图16-7给出了单处理器上带截止时间和惩罚的单位时间任务调度问题的一个例子。在此例中,贪心算法按顺序选择任务
a
1
,
a
2
,
a
3
,
a
4
a_1, a_2, a_3, a_4
a1,a2,a3,a4 ,然后拒绝
a
5
a_5
a5(因为检查到
t
=
4
t=4
t=4 时有
N
4
(
{
a
1
,
a
2
,
a
3
,
a
4
,
a
5
}
)
=
5
N_4( \{ a_1, a_2, a_3, a_4, a_5\} ) = 5
N4({a1,a2,a3,a4,a5})=5 )和
a
6
a_6
a6(因为检查到
t
=
4
t=4
t=4 时有
N
4
(
{
a
1
,
a
2
,
a
3
,
a
4
,
a
6
}
)
=
5
N_4( \{ a_1, a_2, a_3, a_4, a_6\} ) = 5
N4({a1,a2,a3,a4,a6})=5 ),最后接受
a
7
a_7
a7 。最终的最优调度为:
⟨
a
2
,
a
4
,
a
1
,
a
3
,
a
7
,
a
5
,
a
6
⟩
\langle a_2, a_4, a_1, a_3, a_7, a_5, a_6\rangle
⟨a2,a4,a1,a3,a7,a5,a6⟩
总惩罚为 w 5 + w 6 = 50 w_5 + w_6 = 50 w5+w6=50 。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










