四、递归&记忆化

递归

一个函数反复调用自己的过程叫递归。

一个例子：

你有事找A老师，但是A老师说这事不归他管，你得找B老师，	
然后你去找了B老师，B老师说这事不归她管，你得找A老师。
这时候就形成了一个递归过程，你反复使用了“找老师”的操作，但是显而易见，这个例子的是无法解决的，因为这形成了一个递归的死循环。

另一个例子：

怎么样判断一个数是正整数？
或许我们不知道怎么定义一个正整数，但是我们知道以下两个定论：
(1) 1 是正整数
(2) 如果 n 是正整数，那 n+1 也是正整数
基于此，我们就可以判断一个数是不是正整数了。

又一个例子：

数学函数也能定义递归过程，如下是阶乘的数学表达式：
$$n!=\{\begin{array}{l}f(0)=1\\ f(x)=f(x-1)\ast x(1\le x\le n)\end{array}$$
将此公式改写成代码则如下：

	int f(int n){
		if(n == 0)return 1;
		else return f(n - 1) * n;
	}

假如我们现在调用 f (3) ，则可以抽象比喻成下面的例子：

皇上：大臣帮我算一下f(3);
大臣：知县帮我算一下f(2)；
知县：师爷帮我算一下f(1);
师爷翻书一看f(0) = 1;
然后开始上报
师爷上报知县说：f(1) = 1 //f(1) = f(0) * 1
然后知县上报大臣说：f(2) = 2 //f(2) = f(1) * 2
最后大臣上报皇上说：f(3) = 6 //f(3) = f(2) * 3

可以看出递归时，上级函数处于等待下级函数“回话”的过程。虽然浅显易懂，但相对会有很多弊端。弊端将在下一个例子讲解。

最后一个例子：

众所周知斐波那契数的递推式为：
$$fib(n)=\{\begin{array}{l}fib(1)=1\\ fib(2)=1\\ fib(n)=fib(n-1)+f(n-1)(n\ge 3)\end{array}$$
转化为程序则如下：

int fib(int n){
	if(n == 1 || n == 0)return 1;
	else return fib(n - 1) + fib(n - 2);
}

过程如图，弊端十分明显：fib(3)被反复调用了两次，做了大量的无用功。

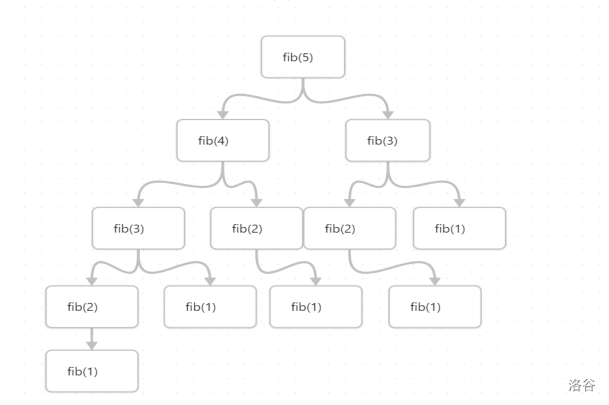
记忆化搜索

接上个例子，我们发现fib(3)被反复调用，并且fib的每一项都是固定不变的，那这样的话我们就可以把前面出现过的所有fib都记录下来，如果某一项有记录，那就直接返回有记录的一项即可，这样就可以避免反复调用同一个函数而浪费大量时间了。
我们用dp[ i ]来记录第i项的斐波那契数，dp初始赋值为-1，如果dp[ i ]有值，就直接返回dp[ i ]，否则就计算并保存dp[ i ]。
如果用上一个程序，在n = 50 时就会花费大量时间，但是下面的程序计算几千几万都会很快。

#include<bits/stdc++.h>  
using namespace std;  
const int p = 1000005;  
long long dp[1000005];  
long long fib(long long n){  
	if(dp[n] != -1)return dp[n];  
	if(n == 1 || n == 0) return dp[n] = 1;  
	//这里借用了C语言的特性：赋值具有返回值  
	else {  
		return dp[n] = (fib(n - 1) + fib(n - 2))% p;  
	}  
}  
int main(){  
	int n;  
	memset(dp, -1, sizeof dp);  
	while(cin >> n){  
		cout << fib(n) << endl;  
	}  
	return 0;  
}

1、计算f(n, x)

已知 $f(x,n)=\sqrt{n+\sqrt{(n-1)+\sqrt{(n-2)+\sqrt{...+2+\sqrt{1+x}}}}}$。
计算 $f(x,n)$ 的值。

输入格式

输入 $x$ 和 $n$。

输出格式

函数值，保留两位小数。

样例输入 #1

4.2 10

样例输出 #1

3.68

你能写出数学函数式吗？
$$f(x,n)=\{\begin{array}{l}\sqrt{1+x},n=1\\ \sqrt{n+f(x,n-1)},n\ge 2\end{array}$$
answer：

double func(double n, double x){
	if(n == 1){
		return sqrt(1+x);
	}
	return (sqrt(n + func(n-1, x)));
}

2、再求f(n,x)

再求 f(x,n)

已知$f(x,n)=\frac{x}{n+\frac{x}{(n-1)+\frac{x}{(n-2)+\frac{⋮}{\cdots +\frac{x}{1+x}}}}}$。

输入格式

第一个数是 $x$ 的值，第二个数是 $n$ 的值。（$x$ 为实数，$n$ 为整数）

输出格式

函数值，保留两位小数。

样例输入 #1

1 2

样例输出 #1

0.40

你能写出来吗？
$$
f(n,x) =
\begin{cases}
\dfrac{x}{1 + x}\ \ \ \ (n = 1)\
\dfrac{x}{n + f(n - 1, x)}\ \ \ \ (n \ge2)

\end{cases}
$$

double func(int n, double x){
	if(n == 1){
		return x/(1+x);
	}
	return x/(n+func(n-1, x));
}

3、小猴吃桃

一只小猴买了若干个桃子。第一天他刚好吃了这些桃子的一半，又贪嘴多吃了一个；接下来的每一天它都会吃剩余的桃子的一半外加一个。第 $n$ 天早上起来一看，只剩下 $1$ 个桃子了。请问小猴买了几个桃子？

输入格式

输入一个正整数 $n$，表示天数。$n\le 30$。

输出格式

输出小猴买了多少个桃子。

样例输入 #1

4

样例输出 #1

22

你能写出来吗？
$$day(n)=\{\begin{array}{l}1，n=1\\ 2\ast [day(n-1)+1]，n\ge 2\end{array}$$

long long func(int n){
	if(n == 1)return 1;
	else return 2*(func(n - 1) + 1);
}

4、Function

对于一个递归函数 $w(a,b,c)$

• 如果 $a\le 0$ 或 $b\le 0$ 或 $c\le 0$ 就返回值$1$。
• 如果 $a>20$ 或 $b>20$ 或 $c>20$ 就返回 $w(20,20,20)$
• 如果 $a<b$ 并且 $b<c$ 就返回$w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c)$。
• 其它的情况就返回 $w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1)$

这是个简单的递归函数，但实现起来可能会有些问题。当 $a,b,c$ 均为 $15$ 时，调用的次数将非常的多。你要想个办法才行。
注意：例如 $w(30,-1,0)$ 又满足条件 $1$ 又满足条件 $2$，请按照最上面的条件来算，答案为 $1$。

输入格式

会有若干行，每行三个数：a，b，c，
$a,b,c\in [-9223372036854775808,9223372036854775807]$ （long long)
并以 $-1,-1,-1$ 结束。

输出格式

输出若干行，每一行格式：
w(a, b, c) = ans

样例输入 #1

1 1 1
2 2 2
-1 -1 -1

样例输出 #1

w(1, 1, 1) = 2
w(2, 2, 2) = 4

你能写出来吗？
$$f(a,b,c)=\{\begin{array}{l}1，ifaorborc=0;\\ \\ f(20,20,20)，ifaorborc\ge 20;\\ \\ f(a,b,c-1)+f(a,b-1,c-1)-f(a,b-1,c)，ifa<bandb<c;\\ \\ f(a-1,b,c)+f(a-1,b-1,c)+f(a-1,b,c-1)-f(a-1,b-1,c-1)，else;\end{array}$$
以下给出部分代码：

long long func(a,b,c){
	if(a < 0 || b < 0 || c < 0)return 1;
	if(a > 20 || b > 20 || c > 20)return func(20, 20, 20);
	if(a < b && b < c)
		return func(a, b, c - 1) + func(a, b - 1, c - 1) - func(a, b - 1, c);
	else 
		return func(a-1,b,c)+func(a-1,b-1,c)+func(a-1,b,c-1)-func(a-1,b-1,c-1);
}

但是显然这个的速度是不够用的，尝试用记忆化搜索改写。

tips：可以用dp{i, j, k}记录，i, j, k，分别表示a, b, c 的状态。