SUPER-ADAM: Faster and Universal Framework of Adaptive Gradients

看了啥：

主要来看看别人是如何证明收敛的，围绕算法SUPER-ADAM 的更新过程和论文后面的证明，（这篇证明比上周的亲切多了，我哭死）仔细看了证明每一步的推导（至于作者如何想出的，还没有去考虑）

又顺了一遍证明，开头几个引理是证明收敛性的关键，这几个引理是直接引用的其他文章，不附带证明。在这开头的引理下，开启我们的引理。证明收敛性之前，多个引理层层递进，用的都是已知条件或者就是上文已经证明的引理或条件。对于放缩用的就是柯西、均值、用已知参数范围放缩、甚者就是狠狠放缩，放的很宽。

---

论文基本信息： 

摘要：为自适应梯度算法设计一个通用的框架。我们通过引入一个包括大多数现有自适应梯度形式的通用自适应矩阵，提出了一个更快、更通用的自适应梯度框架(即Super-Adam)。此框架可以结合动量和方差减少技术。特别是，新框架为自适应梯度方法在非凸环境下的收敛分析提供了支持。

本文的三个贡献：

1：摘要提到的，设计了一个自适应梯度框架，框架可以灵活地结合动量和方差减少技术。

2：在较温和的条件下，我们为非凸环境下的自适应梯度法提供了一种新的收敛分析框架

3：SUPER-ADAM (τ = 1)) 运用momentum-based variance reduced gradient estimator

---

论文一些信息:

自适应矩阵Ht 以一般形式给出  其中，矩阵At包括从具有噪声的随机梯度生成的自适应信息，并且调谐参数λ平衡这些自适应信息与噪声。(Id是单位矩阵）

---

 step9：可以灵活地使用不同的自适应学习速率和不同的随机梯度估计器gt  

---

---

不懂的：

p5:  这个形式怎么就是梯度下降更新了    （先不用管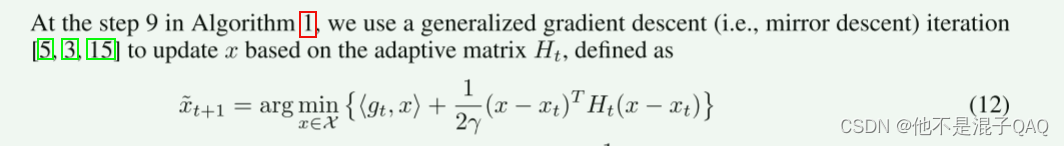

---

 记录：

 回顾一下adam更新过程

Adam的变量包括mt​（一阶矩量，即梯度的指数加权移动平均）和 vt​（二阶矩量，即梯度平方的指数加权移动平均）。 

---

 Young不等式    感觉论文里提到的和这个不太一样诶？

---

逐维学习率  coordinate-wise learning rates 

---