傅里叶变换详解：从级数到变换-CSDN博客

本文深入探讨傅里叶级数和傅里叶变换，包括周期为2π和T的傅里叶级数、傅里叶变换的性质、离散傅里叶变换（DFT）及其快速算法（FFT）。通过实例分析和代码演示，展示了傅里叶变换在连续和离散信号处理中的应用，以及在图像处理中的二维傅里叶变换。最后提到了OpenCV中的getOptimalDFTSize函数在最佳DFT尺寸计算中的作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

3，离散傅里叶变换（DFT）、快速傅里叶变换（FFT）

（5）Demo4——更简单的离散非周期信号

一，傅里叶级数

1，三角函数系

{1, cos x, sin x, cos 2x, sin 2x,......}在[-π，π]上正交

2，周期为2π的傅里叶级数

f在[-π，π]上按段光滑，f周期为2π

$S(x)=\frac{a_0}{2}+\sum _{n>0}(a_ncos\, nx+b_nsin\, nx)$

其中， $a_n=\frac{1}{\pi}\int_{-\pi}^\pi f(x)cos\,nxdx,n\geq 0$ , $b_n=\frac{1}{\pi}\int_{-\pi}^\pi f(x)sin\,nxdx,n> 0$

3，部分和数列

f在[-π，π]上按段光滑，f周期为2π，则

$S_n(x)=\frac{1}{\pi}\int_{-\pi}^\pi f(x+t)\frac{sin(n+\frac{1}{2})t}{2sin\frac{1}{2}t}dt$

证明：

4，贝塞尔不等式（Bessel）

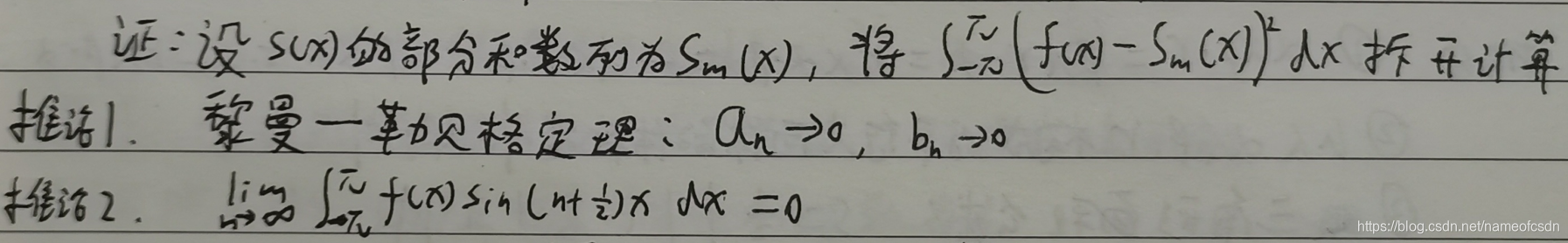
5，傅里叶级数的狄利克雷收敛定理

任意x，f(x+0)+f(x-0)=2S(x)

6，周期为T的傅里叶级数

$S(x)=\frac{a_0}{2}+\sum _{n>0}(a_ncos\, \frac{2\pi}{T}nx+b_nsin\, \frac{2\pi}{T}nx)$

其中， $a_n=\frac{2}{T}\int_{0}^T f(x)cos\,\frac{2\pi}{T}nxdx,n\geq 0$ , $b_n=\frac{2}{T}\int_{0}^T f(x)sin\,\frac{2\pi}{T}nxdx,n>0$

7，傅里叶级数的复数形式

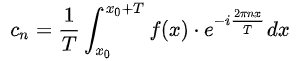
其中 $c_n$ 要么是实数要么是纯虚数

8，Demo1——连续周期信号

先构造函数：（周期为2pi）

$f(x)=\left\{\begin{matrix} 1,-\pi<x<0 \\ -1,0<x<\pi \end{matrix}\right.$

构造点阵，然后画图：

from numpy import *
from matplotlib.pyplot import *
from pylab import *
import math

pi = 3.1415926
x = linspace(-pi * 2, pi * 2, 1000)
y = [1 if int((i + pi * 2) / pi + 1) % 2 == 0 else -1 for i in x]
plot(x, y)
show()

运行结果：

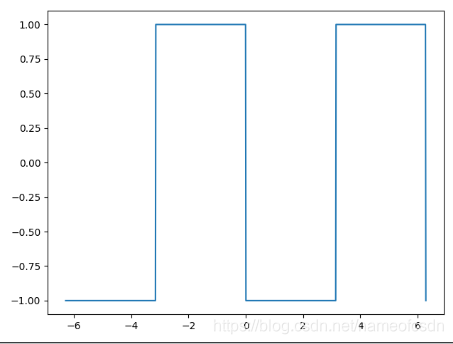
然后计算傅里叶级数：

$S(x)=\sum _{n>0}(b_nsin\, nx)$ ，其中 $b_n=\frac{2((-1)^n-1)}{n\pi}$

当n为偶数时， $b_n$ = 0

然后画图显示傅里叶级数：

s = 0
for n in range(1,100,2):
    bn = ((-1)**n-1)*2/n/pi
    s1 = bn* sin(n*x)
    s += s1
    plot(x, y)
    plot(x, s)
    plot(x, s1)
    show()
    #time.sleep(2)

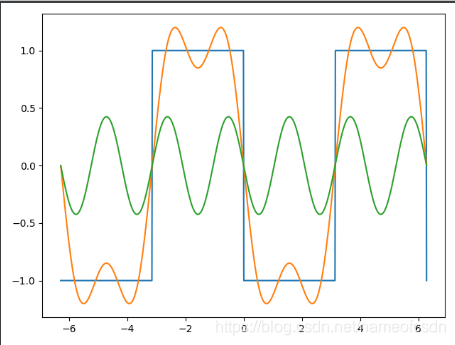
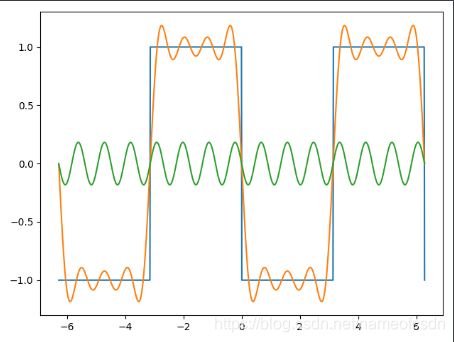
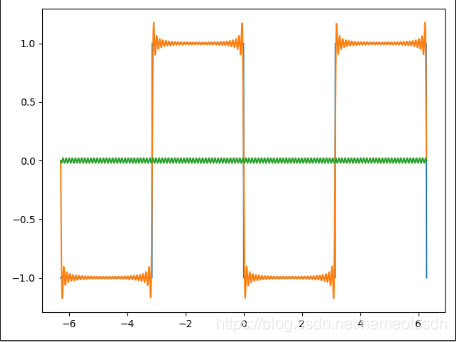
蓝色的是原始函数，绿色的是傅里叶级数的第n项，橙色的是傅里叶级数的前n项和。

当n越来越大时，部分和数列越来越接近原始函数。

二，一维傅里叶变换

1，傅里叶级数的极限

对于非周期函数，可以理解为周期是无穷大。

对上面的式子，我给出了不是特别严谨的数学证明：

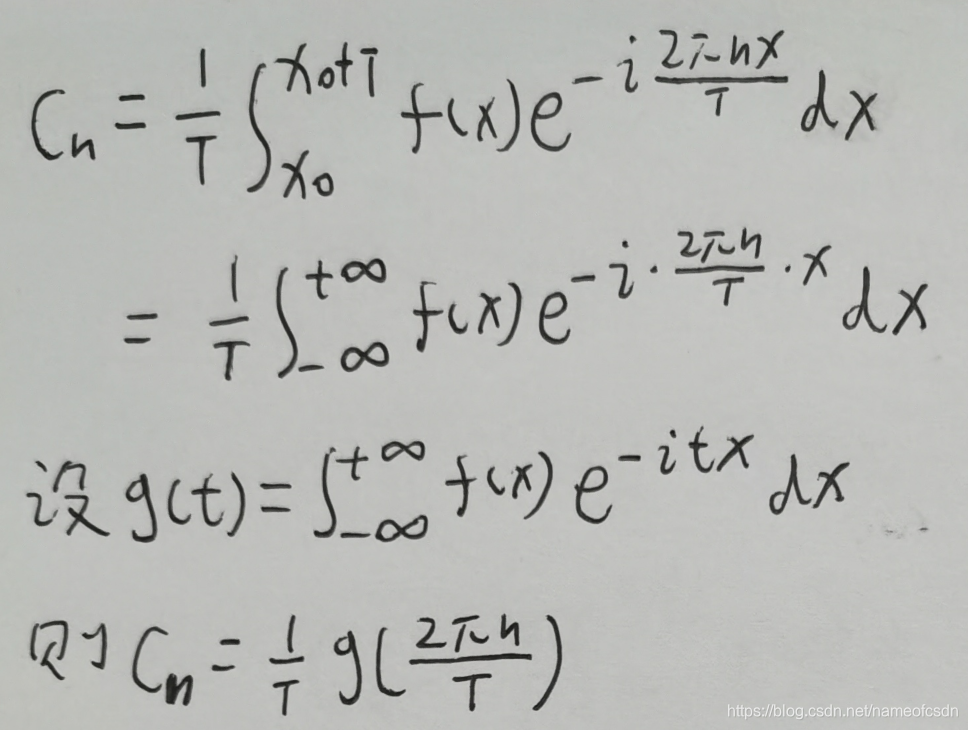
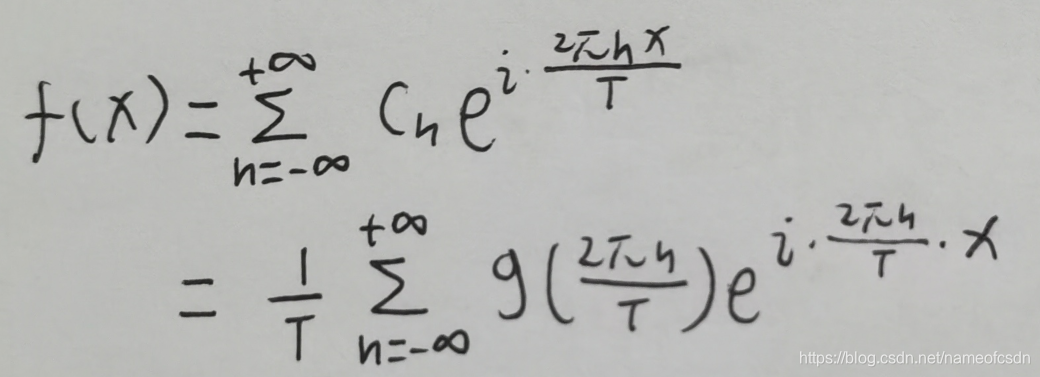
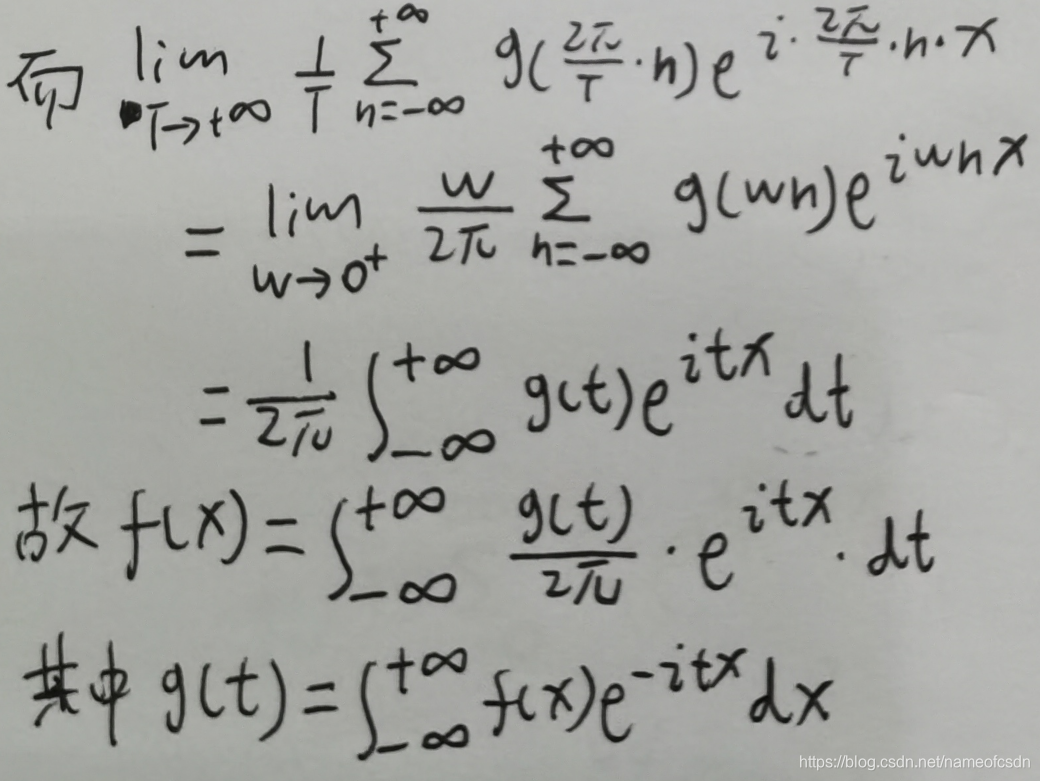
2，傅里叶变换（FT）

傅里叶变换：

$F(\omega)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f(x) e^{-i \omega x} d x$

逆变换：

$f(x)=\int_{-\infty}^{\infty} F(\omega) e^{i \omega x}d\omega$

（1）深入理解FT

把F按照实部和虚部分开表示：

$F(\omega)=F_1(\omega)-iF_2(\omega), F_1(\omega)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f(x) cos(\omega x) dx, F_2(\omega)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f(x) sin(\omega x) dx$

即F1是F的实部，F2是F的虚部。

而实函数一定可以表示成奇函数和偶函数之和，不妨设 $f(x)=f_1(x)+f_2(x)$ ，其中f1是偶函数，f2是奇函数，则 $F_1(\omega)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f_1(x) cos(\omega x) dx, F_2(\omega)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f_2(x) sin(\omega x) dx$

所以f中的偶函数分量经过傅里叶变换之后会得到实部，奇函数分量经过傅里叶变换之后会得到虚部。

另一方面，F1显然是偶函数，F2显然是奇函数，所以也可以说，f中的偶函数分量经过傅里叶变换之后会得到偶函数，奇函数分量经过傅里叶变换之后会得到奇函数。

而对于逆变换：

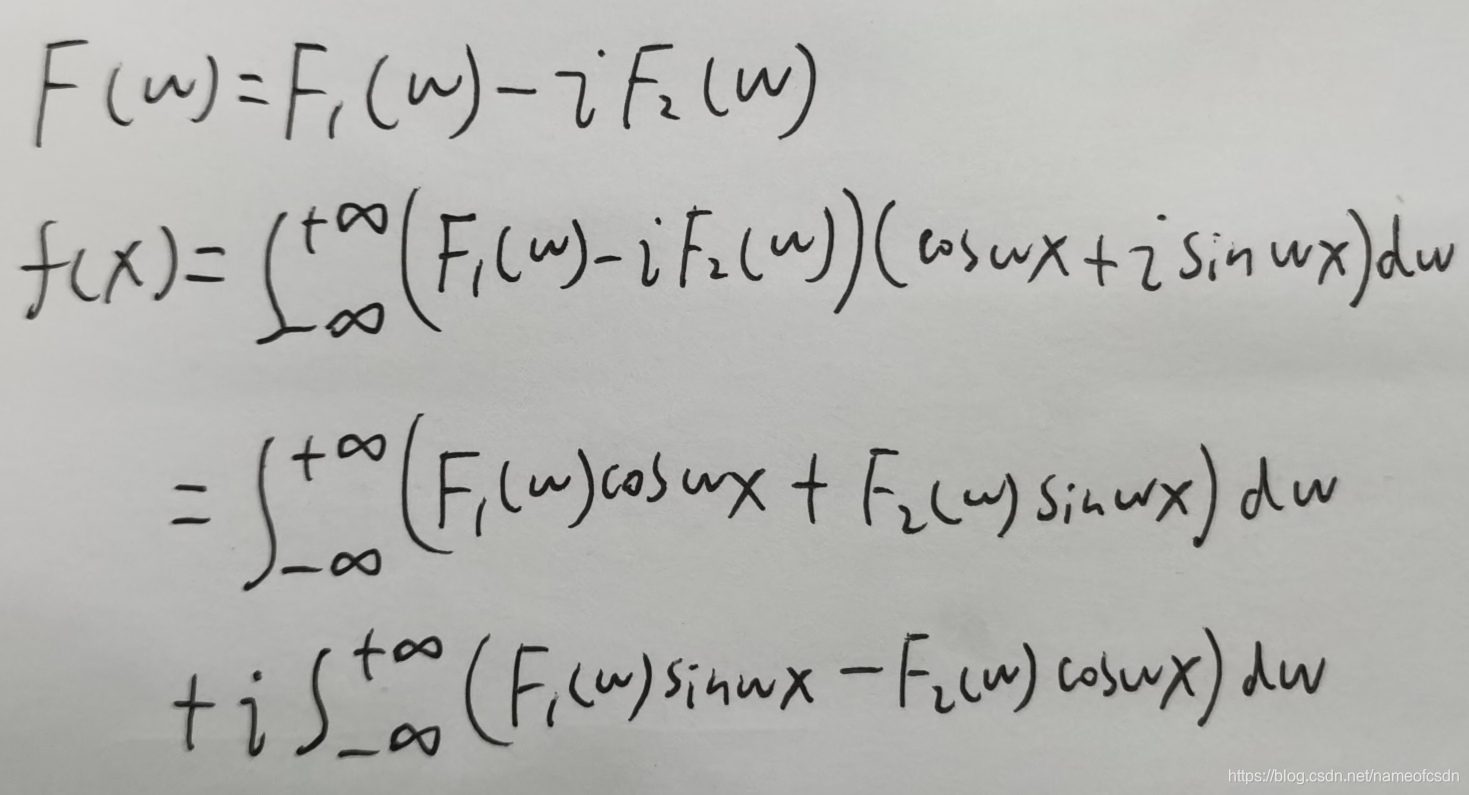
因为F1是偶函数，F2是奇函数，所以也能推导出f的虚部为0，最终得到：

$f(x)=\int_{-\infty}^{\infty} (F_1(\omega) cos(\omega x)+F_2(\omega) sin(\omega x))d\omega$

即F中的偶函数分量经过逆变换之后会得到偶函数，奇函数分量经过逆变换之后会得到奇函数。

（2）Demo2——连续非周期信号

$f(x)=\left\{\begin{matrix} 1,-\pi<x<0 \\ -1,0<x<\pi \end{matrix}\right.$

import numpy
from pylab import *

x = numpy.lins