目录
一,不同元素的划分——斯特林数(Stirling数)
1,第一类斯特林数


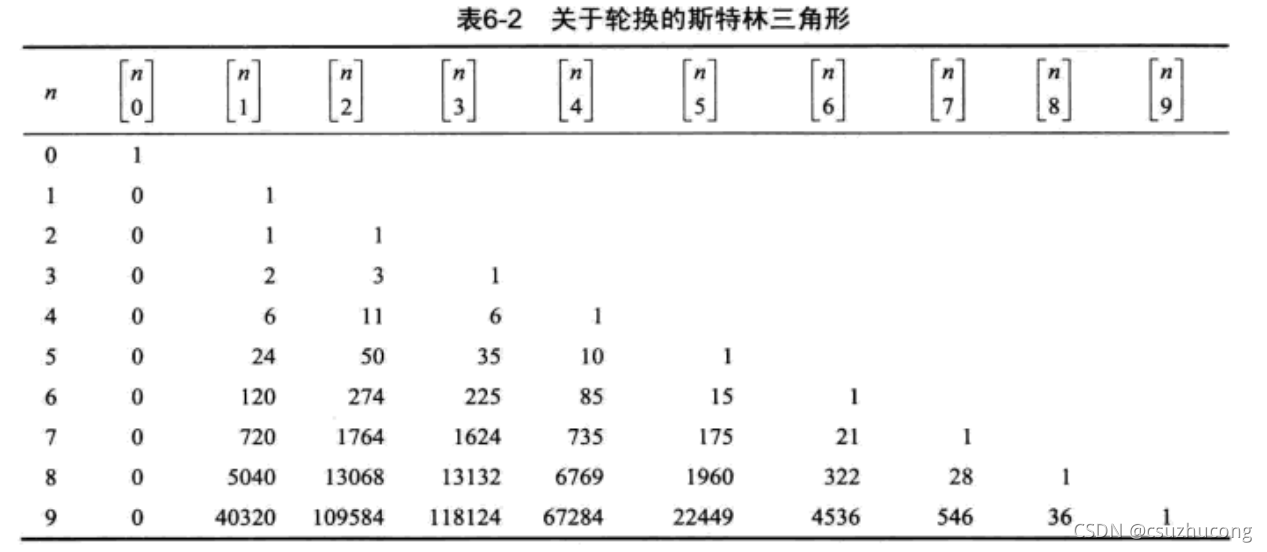
2,第二类斯特林数

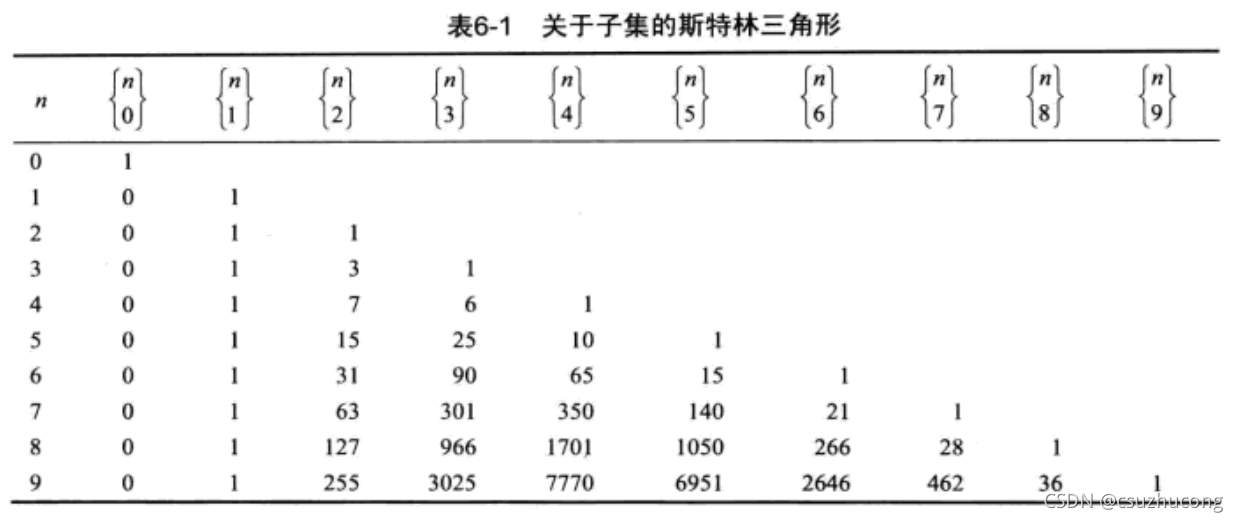
3,斯特林数的性质
二,贝尔数
1,贝尔数
Bn是基数为n的集合划分数目。

其中S是第二类斯特林数
例如,
B1=1,
B2=1+1=2,
B3=1=3+1=5,
B4 = 1+7+6+1 = 15,
B5=1+15+25+10+1=52
2,贝尔数的递推式


3,OJ实战
FZU 1570 集合划分问题
题目:
Description
n个元素的集合{1,2,...,n}可以划分若干个非空子集。例如,当n=4时,集合{1,2,3,4}可以划分为15个不同的非空子集如下:
{
{1},{2},{3},{4}},
{
{1,2},{3},{4}},
{
{1,3},{2},{4}},
{
{1,4},{2},{3}},
{
{2,3},{1},{4}},
{
{2,4},{1},{3}},
{
{3,4},{1},{2}},
{
{1,2},{3,4}},
{
{1,3},{2,4}},
{
{1,4},{2,3}},
{
{1,2,3},{4}},
{
{1,2,4},{3}},
{
{1,3,4},{2}},
{
{2,3,4},{1}},
{
{1,2,3,4}}
给定正整数n(1<=n<=20),计算出n个元素的集合{1,2,...,n} 可以化为多少个不同的非空子集。
Input
多组输入数据,每组数据1行,表示元素个数n.
Output
对于每组数据,输出一行一个数,表示不同的非空子集的个数。
Sample Input
2
4
Sample Output
2
15
用递归法求出第二类Stirling数,然后求和得到sum即为答案。
代码:
#include<iostream>
using namespace std;
const int l = 21;
long long Stirling[l][l];
long long sum[l];
void getStirling()
{
for (int i = 0; i < l; i++)
{
sum[i] = 0;
for (int j = 0; j < l; j++)Stirling[i][j] = 0;
}
Stirling[0][0] = 1;
for (int i = 1; i < l; i++)for (int j = 1; j <= i; j++)
{
Stirling[i][j] = Stirling[i - 1][j - 1] + Stirling[i - 1][j] * j;
sum[i] += Stirling[i][j];
}
}
int main()
{
getStirling();
int n;
while (cin >> n)cout << sum[n] << endl;
return 0;
}4,有序贝尔数
其中S是第二类斯特林数
例如,OB(0)=1, OB(1)=1, OB(2)=3, OB(3)=13, OB(4)=75
5,有序贝尔数的递推式
三,相同元素的划分
HDU 2566 统计硬币(常数时间解法)
题目:
Description
假设一堆由1分、2分、5分组成的n个硬币总面值为m分,求一共有多少种可能的组合方式(某种面值的硬币可以数量可以为0)。
Input
输入数据第一行有一个正整数T,表示有T组测试数据;
接下来的T行,每行有两个数n,m,n和m的含义同上。
Output
对于每组测试数据,请输出可能的组合方式数;
每组输出占一行。
Sample Input
2
3 5
4 8
Sample Output
1
2
首先判断n*5>=m是否成立,如果不成立的话,方案数就是0了
如果n*5>=m,那么5分硬币的数量可能是0,1,2......m/5
假设5分硬币的数目是i,0<=i<=m/5
那么现在就是考虑,n-i个1分和2分的硬币组成m-i*5分有多少种方案?
规律很简单,如果n-i<=m-i*5<=(n-i)*2那么方案数为1,否则为0
综上所述,如果n*5<m那么方案数为0,否则,方案数是闭区间[0,m/5]和闭区间[(m-n*2)/3.0,m-n/4]的交集所包含的整数的数量,之间用交集的上界减下界即可。
代码:
#include <iostream>
using namespace std;
int f(int n, int m)
{
if (n * 5 < m || m < n)return 0;
int up = n * 5, down = 0;
if ((m - n) / 4 < up)up = (m - n) / 4;
if ((m - n * 2) >= 3)down = (m - n * 2 + 2) / 3;
return up-down+1;
}
int main()
{
int t, n, m;
cin >> t;
while (t--)
{
cin >> n >> m;
cout << f(n, m) << endl;
}
return 0;
}POJ 1664 放苹果
题目:
Description
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
Input
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
Output
对输入的每组数据M和N,用一行输出相应的K。
Sample Input
1
7 3
Sample Output
8
这个题目自然是递归,但不是所有人的递归式都是一样的。
假设本题对应的答案是list[n][m],n,m非负,
那么首先,当n为0时list[0][i] = (i == 0);
其次,找递归式。
如果这n个盘子里面,存在空盘子,那么去掉它,就变成“把m个相同的苹果放入n-1个相同的盘子”这个子问题了。
否则,每个盘子都至少有1个苹果,那么去掉这n个苹果,就变成“把m-n个苹果放入n个相同的盘子”这个子问题了。
所以,递归式就是list[n][m]=list[n-1][m]+list[n][m-n]
代码:
#include<iostream>
#include<stdio.h>
using namespace std;
const int l = 11;
int list[l][l];
void getList()
{
for (int i = 0; i < l; i++)list[0][i] = (i == 0);
for (int i = 1; i < l; i++)for (int j = 0; j < l; j++)
{
list[i][j] = list[i - 1][j];
if (j >= i)list[i][j] += list[i][j - i];
}
}
int main()
{
getList();
int t, m, n;
scanf("%d", &t);
while (t--)
{
scanf("%d%d", &m, &n);
printf("%d\n", list[n][m]);
}
return 0;
}九度OJ 1084 整数拆分
题目描述:
一个整数总可以拆分为2的幂的和,例如:
7=1+2+4
7=1+2+2+2
7=1+1+1+4
7=1+1+1+2+2
7=1+1+1+1+1+2
7=1+1+1+1+1+1+1
总共有六种不同的拆分方式。
再比如:4可以拆分成:4 = 4,4 = 1 + 1 + 1 + 1,4 = 2 + 2,4=1+1+2。
用f(n)表示n的不同拆分的种数,例如f(7)=6.
要求编写程序,读入n(不超过1000000),输出f(n)%1000000000。
输入:
每组输入包括一个整数:N(1<=N<=1000000)。
输出:
对于每组数据,输出f(n)%1000000000。
样例输入:
7
样例输出:
6
这个题目找递推式的方法,和 POJ - 1664 放苹果 本质差不多
代码:
#include<iostream>
using namespace std;
int list[1000001];
int main()
{
list[1] = 1, list[2] = 2;
for (int i = 3; i <= 1000000; i++)list[i] = (list[i - 2] + list[i / 2]) % 1000000000;
int n;
while (cin >> n)cout << list[n] << endl;
return 0;
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








