环路检测

目录

一，无向图

HDU 1272 小希的迷宫

力扣 1559. 二维网格图中探测环

力扣 261. 以图判树

二，有向图

力扣 207. 课程表

三，环路长度

力扣 2127. 参加会议的最多员工数

---

一，无向图

判断一个无向图是否有环，可以用并查集，在merge2个节点时，如果发现2个节点已经是同一个祖先，则表示已经形成环。

HDU 1272 小希的迷宫

Description

上次Gardon的迷宫城堡小希玩了很久（见Problem B），现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样，首先她认为所有的通道都应该是双向连通的，就是说如果有一个通道连通了房间A和B，那么既可以通过它从房间A走到房间B，也可以通过它从房间B走到房间A，为了提高难度，小希希望任意两个房间有且仅有一条路径可以相通（除非走了回头路）。小希现在把她的设计图给你，让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子，前两个是符合条件的，但是最后一个却有两种方法从5到达8。 

Input

输入包含多组数据，每组数据是一个以0 0结尾的整数对列表，表示了一条通道连接的两个房间的编号。房间的编号至少为1，且不超过100000。每两组数据之间有一个空行。 
整个文件以两个-1结尾。 
Output

对于输入的每一组数据，输出仅包括一行。如果该迷宫符合小希的思路，那么输出"Yes"，否则输出"No"。 
Sample Input

6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0

-1 -1
Sample Output

Yes
Yes
No

代码：

#include<iostream>
#include<cstring>
using namespace std;

int fa[100001];
int num[100001];
int sum;

int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

int main()
{
	ios_base::sync_with_stdio(false);
	int m, n,max1, max2;
	while (1)
	{
		bool flag = true;
		sum = 0, max1 = 0, max2 = 0;
		while (cin >> m >> n)
		{
			if (m == 0 && n == 0)break;
			if (m == -1 && n == -1)return 0;
			if (max2 < m) max2 = m;
			if (max2 < n) max2 = n;
			for (int i = max1 + 1; i <= max2; i++)fa[i] = -1;
			max1 = max2;
			if (fa[m] >= 0 && fa[n] >= 0)
			{
				if (find(m) == find(n))flag = false;
				else
				{
					num[find(n)] += num[find(m)];
					fa[find(m)] = find(n);
				}
			}
			else
			{
				if (fa[m] >= 0)
				{
					fa[n] = m;
					num[find(m)]++;
				}
				else if (fa[n] >= 0)
				{
					fa[m] = n;
					num[find(n)]++;
				}
				else
				{
					fa[m] = m;
					fa[n] = m;
					num[m] = 2;
					sum++;
				}
				sum++;
			}
		}
		if (flag && num[find(max2)] == sum)cout << "Yes";
		else cout << "No";
		cout << endl;
	}
	return 0;
}

力扣 1559. 二维网格图中探测环

给你一个二维字符网格数组 grid ，大小为 m x n ，你需要检查 grid 中是否存在 相同值 形成的环。

一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 相同的值 。

同时，你也不能回到上一次移动时所在的格子。比方说，环  (1, 1) -> (1, 2) -> (1, 1) 是不合法的，因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。

如果 grid 中有相同值形成的环，请你返回 true ，否则返回 false 。

示例 1：

输入：grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
输出：true
解释：如下图所示，有 2 个用不同颜色标出来的环：

示例 2：

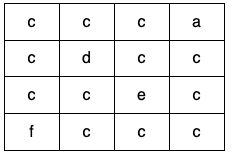
输入：grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
输出：true
解释：如下图所示，只有高亮所示的一个合法环：

示例 3：

输入：grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
输出：false
 

提示：

m == grid.length
n == grid[i].length
1 <= m <= 500
1 <= n <= 500
grid 只包含小写英文字母。

class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	bool containsCycle(const vector<vector<char>>& matrix) {
		col = matrix[0].size();
		map<int, vector<int>>m;
		for (int i = 1; i < matrix.size(); i++)for (int j = 0; j < matrix[0].size(); j++)
			if (matrix[i][j] == matrix[i - 1][j])m[id(i, j)].push_back(id(i - 1, j)),m[id(i-1, j)].push_back(id(i, j));
		for (int i = 0; i < matrix.size(); i++)for (int j = 1; j < matrix[0].size(); j++)
			if (matrix[i][j] == matrix[i][j - 1])m[id(i, j)].push_back(id(i, j - 1)),m[id(i, j-1)].push_back(id(i, j));
        if(m.empty())return false;
		return HasUndirectedCircle(m);
	}
	int col;
};

力扣 261. 以图判树

给定编号从 0 到 n - 1 的 n 个结点。给定一个整数 n 和一个 edges 列表，其中 edges[i] = [ai, bi] 表示图中节点 ai 和 bi 之间存在一条无向边。

如果这些边能够形成一个合法有效的树结构，则返回 true ，否则返回 false 。

示例 1：

输入: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
输出: true

示例 2:

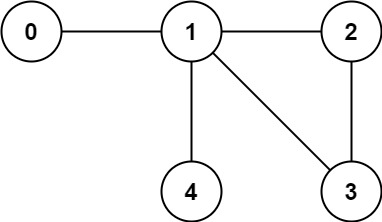
输入: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
输出: false

提示：

• 1 <= n <= 2000
• 0 <= edges.length <= 5000
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 不存在自循环或重复的边

class Solution {
public:
    bool validTree(int n, vector<vector<int>>& edges)
    {
        if(edges.empty())return n==1;
        vector<UndirectedEdge<int>>v;
        for (auto vi : edges)v.push_back(UndirectedEdge<>(vi));
        UndirectedGraphData<> g(v);
        int num;
        KruskalMinCostTree(n,v,num);
        return !HasUndirectedCircle(g) && num==1;
    }
};

二，有向图

用DFS判断有向图是否有环。

力扣 207. 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。
 

提示：

1 <= numCourses <= 105
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同

题意：

输入点的数量n 和 由边组成的向量，描述了一个有向图，判断它有没有环。

思路：

DFS，往下遍历的时候用visitt标记，往上回溯的时候擦除标记，如果遇到已标记的说明有环。

从每个点开始遍历，都没有环的话，就没有环。

但是这样效率太低，所以我再用一个flag标记，表示曾经访问过，也就不需要作为起点开始遍历了。

代码：

class Solution {
public:
	bool canFinish(vector<vector<int>>& diag, int loc) {
		if (visitt[loc] == 1)return false;
		if (flag[loc] == 1)return true;
		visitt[loc] = 1, flag[loc] = 1;
		for (int i = 0; i < diag[loc].size(); i++)
		{
			if (!canFinish(diag, diag[loc][i]))return false;
		}
		visitt[loc] = 0;
		return true;
	}
	bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
		vector<int>tmp;
		vector<vector<int>>diag;
		for (int i = 0; i < numCourses; i++)
		{
			diag.insert(diag.end(), tmp);
			visitt[i] = 0, flag[i] = 0;
		}
		for (int i = 0; i < prerequisites.size(); i++)
		{
			diag[prerequisites[i][0]].push_back(prerequisites[i][1]);
		}
		for (int i = 0; i < numCourses; i++)
		{
			if (flag[i])continue;
			cout << i;
			if (!canFinish(diag, i))return false;
		}
		return true;
	}
private:
    map<int, int>visitt;//单次访问标记
    map<int, int>flag;//所有访问标记
};

三，环路长度

力扣 2127. 参加会议的最多员工数

一个公司准备组织一场会议，邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子，可以坐下 任意数目 的员工。

员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工，每位员工 当且仅当 他被安排在喜欢员工的旁边，他才会参加会议。每位员工喜欢的员工 不会 是他自己。

给你一个下标从 0 开始的整数数组 favorite ，其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。

示例 1：

输入：favorite = [2,2,1,2]
输出：3
解释：
上图展示了公司邀请员工 0，1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议，因为员工 2 没办法同时坐在 0，1 和 3 员工的旁边。
注意，公司也可以邀请员工 1，2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。

示例 2：

输入：favorite = [1,2,0]
输出：3
解释：
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示：
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。

示例 3：

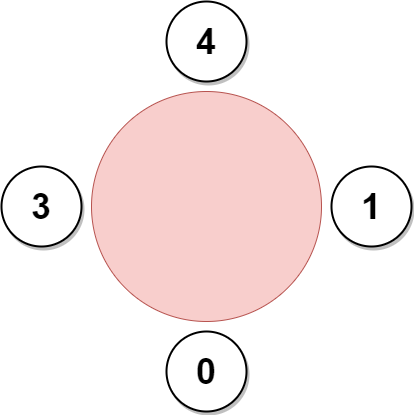
输入：favorite = [3,0,1,4,1]
输出：4
解释：
上图展示了公司可以邀请员工 0，1，3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加，因为他喜欢的员工 0 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。

提示：

• n == favorite.length
• 2 <= n <= 105
• 0 <= favorite[i] <= n - 1
• favorite[i] != i

思路：

首先我们知道，答案只有2种情况，要么就是1个长度为n的大环，n>2，有没就是k个长度为2的小环，每个环的2个节点后面还可以各自接一条单链路。

所以第一步，我们用并查集把所有节点串起来，此时每个集合一定刚好含有一个环。

于是我们遍历每一个环，计算长度，最大值就是问题答案的第一种情况。

接下来我们只需要把所有大环所在集合全部抛弃，把所有小环的2条边删除并求出以这2个点为端点的最长路径，所以最长路径的和就是问题答案的第二种情况。

PS：题目和CSU 1793 Outing有点像，但解法差别挺大的，只是都用了并查集。

代码：

class Solution {
public:
	int maximumInvitations(vector<int>& fa) {
		Union un(fa.size());
		for (int i = 0; i < fa.size(); i++)un.merge(i, fa[i]);
		vector<int> rs = un.getRoots();
		int ans = 0;
		for (auto r : rs) {
			int x = fa[r], s = 1;
			while (x != r)x = fa[x], s++;
			ans = max(ans, s);
			if (s == 2)fa[fa[r]] = fa[r], fa[r] = r; //炸环
		}
		return max(ans, sumOfLongestPath(fa));
	}
	int sumOfLongestPath(vector<int>& fa) {
		Union un2(fa.size());
		map<int, int>sons;
		for (int i = 0; i < fa.size(); i++) {
			un2.merge(i, fa[i]);
			if (fa[i] != i)sons[fa[i]]++;
		}
		map<int, int>m;//统计炸环后的最长链长度
		dpAns.clear();
		for (int i = 0; i < fa.size(); i++)if (sons[i] == 0) {
			int r = un2.find(i);
			if (fa[r]==r)m[r] = max(m[r], dp(fa, i));
		}
		int s = 0;
		for (auto mi : m)s += mi.second;
		return s;
	}
	int dp(vector<int>& fa, int id) {
		if (fa[id] == id)return 1;
		if (dpAns[id])return dpAns[id];
		return dpAns[id] = dp(fa, fa[id]) + 1;
	}
	map<int, int>dpAns;
};