跨领域的抽象概念

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家：点击跳转

〇，前言

本文收录总结我个人知道的一些抽象概念，这些概念在不同的领域使用同一个名字，在不同的领域中乍看含义并不一样，但是深思之后却又能找到深刻的联系。

一，对称性

1，几何中的对称性

（1）轴对称

（2）中心对称

2，物理中的对称性

由于我的物理学习只停留在高考之前，所以我只能以在网上复制一段，我本人也不是完全懂里面的细节。

诺特定理：如果一个物理系统具有某种连续对称性，那么这个系统存在一个相应的守恒定律。

例如，如果一个系统的拉格朗日函数在时间平移下不变，那么这个系统将具有能量守恒的性质；如果系统在空间平移下不变，那么动量守恒；如果系统在空间旋转下不变，那么角动量守恒。

3，组合数学中的轮换对称性

组合数学中，有很多结构上的对称性。

（1）复原魔方单面

如果你学习了一个公式，使得魔方无论怎么打乱再给你，你都有办法复原红色面，那么，你就一定拥有一个能力，魔方无论怎么打乱再给你，你都有办法复原绿色面。

所以我们说，对于复原魔方单面这个问题，红色和绿色具有对称性。

更进一步，我们可以说，复原魔方单面这个问题，任意两个颜色之间都具有对称性。

（2）复原魔方对立两面

魔方的固定对立色是（白黄）（绿蓝）（红橙）

如果你学习了一个公式，使得魔方无论怎么打乱再给你，你都有办法复原白黄两面，那么，你就一定拥有一个能力，魔方无论怎么打乱再给你，你都有办法复原绿蓝两面。

更进一步，我们可以说，复原魔方对立两面这个问题，（白黄）（绿蓝）（红橙）三组之间任意两组都具有对称性。

（3）复原魔方相邻两面

如果你学习了一个公式，使得魔方无论怎么打乱再给你，你都有办法复原红白两面，那么，你就一定拥有一个能力，魔方无论怎么打乱再给你，你都有办法复原绿橙两面。

我们可以说，红白两面和绿橙两面具有对称性。

但是，我们不能说红白两面和白黄两面具有对称性。

（4）轮换对称性

上面三个关于魔方的例子，都可以总结为轮换对称性，这个在组合数学中很常见。

对于不同的问题，什么叫轮换，其实是不一样的。

对于我上面的三个例子，轮换就是不操作魔方，只把整个魔方的朝向调整一下，这是比较简单的一种轮换，魔方中有很多更复杂的轮换，可以在我的魔方系列文章中深挖一下。

（5）数独中的轮换对称性

我在旋转数独这个puzzle中给出的如下的解法：

• 单个九宫格可以填充的数字就填充
• 选择一个出现较多的数字，把它的9个位置都确定下来
• 选择一个数字较多的九宫格，确定和它在同一行的2个九宫格，把这3个九宫格都移到第一行
• 剩下的6个九宫格里面，再选择一个数字较多的九宫格，确定和它在同一行的2个九宫格，把这3个九宫格都移到第二行（第一行的3个九宫格位置不动）
• 只根据行的信息和单个九宫格的信息，可以填充的数字就填充
• 第一行的3个九宫格位置固定不动，让第二行的3个九宫格之间互换，再让第三行的3个九宫格之间互换，使得数独有解
• 直接完成数独

其实这里的逻辑是基于标准数独的轮换对称性：

把9个九宫格看成3行3列的矩阵，完整的数独（填充了81个数字且满足数独的规则）交换任意2行得到的仍然是完整的数独，交换任意2列得到的也仍然是完整的数独。

 （6）波利亚计数

波利亚计数参考这里。

这个神奇且强大的定理，让我对“对称性”的看法，从模糊的概念，变成有深刻内涵的科学术语。

（7）方旋矩理1

最强大脑第12季的项目，规则如下：

5种颜色各25个块，构成5*5*5的立方体。

操作方式和五阶魔方一样，打乱之后复原，使得每一层的25个块同色。

显然，第一个问题就是思考5个颜色从高到低怎么排。

首先，很显然中间层的颜色是确定的，因为最中间的块是不动的，例如上图就是蓝色块，我们称之为中心色。

其次，类比五阶魔方的六个中心块，这6个块是一个封闭的集合，所以一定是4个中心色加上另外2个颜色的块各1个，例如上图就是红色和绿色，我们称之为两端色，剩下的白色和黄色我们称之为夹心色。

最后，五种颜色具体怎么排布呢？是四种组合都可以吗？

这里根据轮换对称性，不妨设第二层就是固定白色，第四层就是固定黄色，只有2个两端色是位置排布是不确定的。

这里是如何轮换对称的？很简单，只需要5次旋转180的操作，就可以把整个立方体上下颠倒。

那么，在此基础上，是否可以不妨设第一层就是固定红色？其实这个问题的答案取决于，一个已经复原的立方体，能不能通过有限次操作，只把第一层和第五层单独交换？

由于没法实操，只能冥想，我暂时不确定这个独立的小问题的答案。

那么，在不知道这个答案的情况下，我们对方旋矩理确定颜色排布这个问题的答案总结下来就是：首先确定中心色和2个两端色和2个夹心色，指定2个夹心色的任意排布即可，唯一不确定的就是2个两端色怎么排布，整个立方体仅有的2种完整颜色排布方案至少有一种是可达状态。

4，桌游中的轮换对称性

桌游中也存在各种形式的轮换对称性，有一些桌游中的对称性规律和策略无关，而我下面列举的，都是轮换对称性会影响策略的例子。

（1）璀璨宝石

璀璨宝石规则参考这里。

宝石中一共有5种颜色，有的卡牌是5张一组，具有轮换对称性，

比如：

再比如：

而有的卡牌不具有轮换对称性，比如：

用置换群来表达的话，上面的5分牌和4分牌都是1个5阶群，而下面的2分牌是1个3阶群，2个1阶群。

由于黑白红处于1个3阶群中，蓝绿各处于1个1阶群中，所以很多宝石策略都会把5个颜色分成2个阵营，即蓝绿阵营和黑白红阵营。

（2）香料物语

略。

香料物语参考这里。

5，高阶轮换对称性

（1）方旋矩理2

上文《方旋矩理1》中，我们得到了两端色是红色和绿色，夹心色是黄色和白色。

只根据“可以把整个立方体上下颠倒”这个轮换对称性，我们就可以得到“不妨设第二层就是固定白色，第四层就是固定黄色，只有2个两端色的排布不确定”。

其实我们也可以得到“不妨设第一层就是固定红色，第五层就是固定绿色，只有2个夹心色的排布不确定”。

那么，这2种选择哪一种来作为方旋矩理确定颜色排布的阶段性成果总结呢？

答案是都可以，不妨设就用第一种。

这就是更高阶的一种轮换对称性。

二，不妨设

所有的不妨设，都是对称性。

1，方旋矩理3

上文的《方旋矩理1》中，根据轮换对称性得到“不妨设第二层就是固定白色，第四层就是固定黄色，只有2个两端色的排布不确定”。

上文的《方旋矩理2》中，则是更高阶的轮换对称性。

这2处我都用到了不妨设。

2，齐次性

证明：

首先，如果xy<=0，则不等式成立。

其次，如果xy>0，则不妨设x>0 y>0

最后，如果x>0 y>0，则不妨设xy=1

这里，我们又用了2次不妨设。

3，变量的强对称性

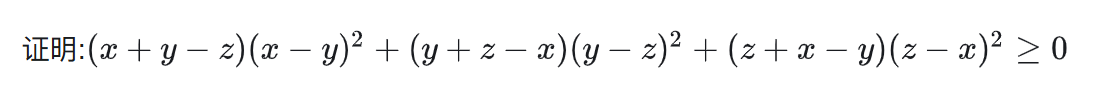
这里的x y z是两两对称的，所以不妨设x>=y>=z

4，变量的弱对称性

这里不妨设a>=b>=c就是错的，但是不妨设a>=b且a>=c就是对的。

三，等价

这个概念在极其多的领域中应用，表面上看起来在不同领域中含义都不一样，五花八门，但实际上应该都可以抽象成离散数学中的等价。

1，等价的题目

老师经常说，这2个题目不是一样的吗？这2个题目有什么区别吗？

这就是2个不同的题目个体具有等价性。

二元关系参考这里。

一个大概的二元关系模型是，用多维空间中的点表示一个题目的解法，如果2个点距离小于某个阈值，则连一条边。

如果这个阈值设置的比较小，就会形成自反、对称、传递、不连通的二元关系。

如果这个阈值设置的比较大，就会形成自反、对称、传递、连通的二元关系（平凡等价关系）。

这两种二元关系，都可以叫等价关系。当然，平凡等价关系不太适合用于描述题目之间的等价关系。

2，等价的什么？

持续更新中，欢迎读者留言补充

四，相似

怎么样算相似呢？相似可以描述哪些对象呢？数值，外观，逻辑，等等

王博老师的培训课给了我启发。

1，相似的题目

怎么样的2个题目算是相似的题目？

（1）只有数字不同的题目

很多人第一反应应该就是，题目完全相同，只有数字不一样的2个题目，肯定是相似题目，实际上真的如此吗?我们看一下2个例子。

题目一：

x+y=1
x*y=-2
求(x^2024+y^2024)%7

解法：

求解方程组，有2个解：
x=-1,y=2
x=2,y=-1
所以(x^2024+y^2024)%7=(2^2024 - 1)%7=3

题目二：

x-y=2
x*y=7
x>0
求(x^2024+y^2024)%7

解法：

求解方程组，有2个解，满足x>0的只有x=2*sqrt(2)+1, y=2*sqrt(2)-1这一个解。
所以首先，(x^2024+y^2024)显然是一个整数。
其次：

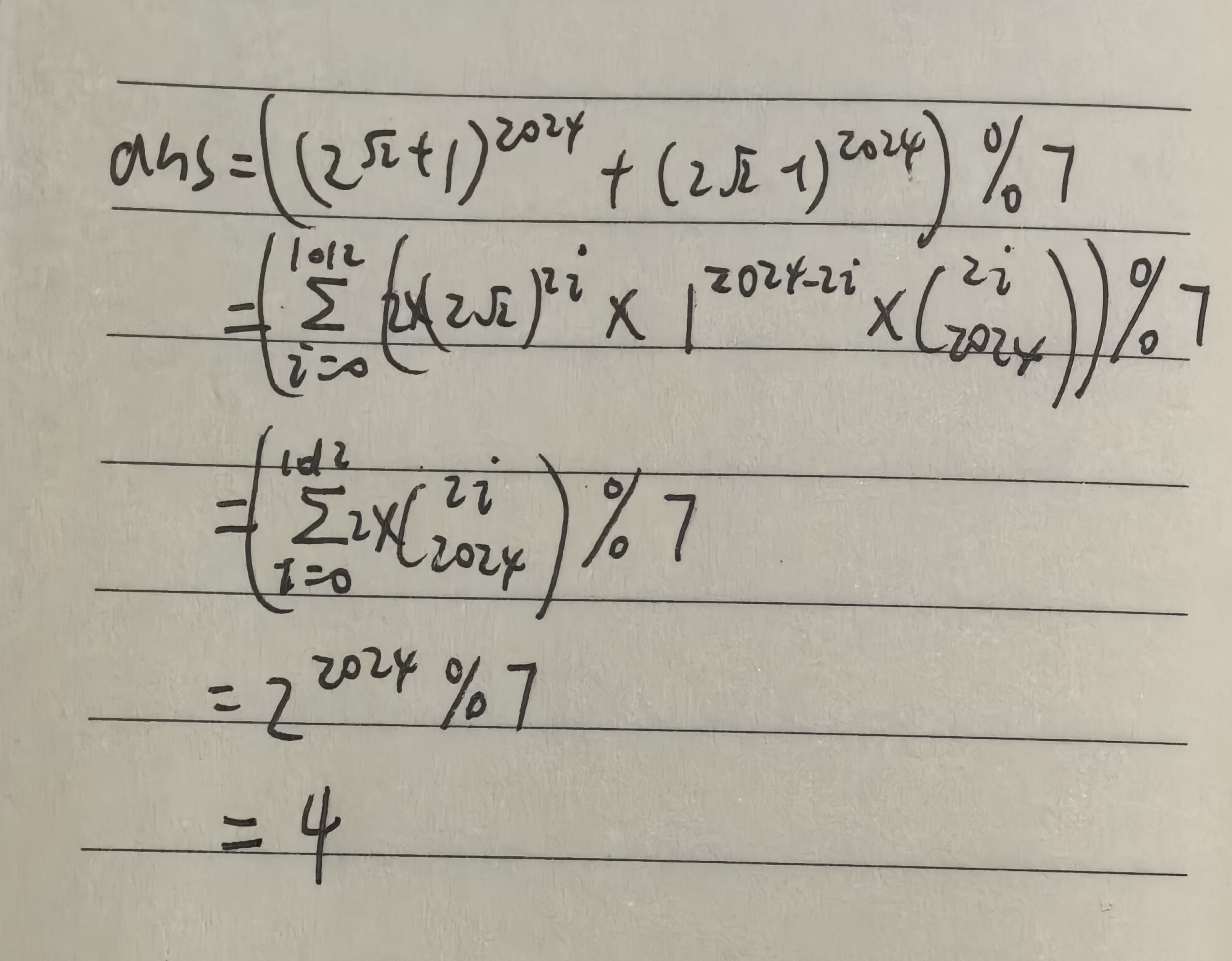
题目三：

x-y=1
x*y=1
x>0
求(x^2024+y^2024)%7

解法：

求解方程组，有2个解，满足x>0的只有x=(sqrt(5)+1)/2, y=(sqrt(5)-1)/2这一个解。
所以首先，(x^2024+y^2024)显然是一个整数。
其次：

这个比上一题更加的复杂，但是也确实有办法手算出来。

所以，读者认为这3个题目相似吗？

严谨的说，应该是题干相似，解法不相似，如果把题目理解成题干+解法，那么显然这3个题目并没有想象中的那么相似。

2，相似的游戏

举一个抽象程度比较高的相似的例子：回合制贪吃蛇 里面的霸屏问题，和2048最大分数 里面的达成最大分数问题，就很相似。

这种相似，是抽象程度比较高的，比较复杂的一种相似。这种相似，主要是核心难点和启发式策略的相似，即固定矩形空间内的排兵布阵，动态调整，最终占满。

而2048和数字消除问题里面的Threes的相似，就是抽象程度比较低的一种相似。这种相似，主要是规则的相似。

五，结构化

1，结构化数据

2，结构化游戏

六，算法、遗忘算法、解空间、对象空间

1，算法

一个魔方公式也可以看做一个算法

这里可能涉及停机问题和公理系统的可判定性之间的关系

2，遗忘算法

3，解空间

参考

七，元

另外一篇文章中的元剪切过来

1，元算法

元算法，即基于算法的算法。

比如算法的轴对称算法。

八，阶

九，自我指涉

十，离散和连续

十一，反演、对偶、共轭

参考数据变换、反演、对偶、共轭

十二，全文总结

本文的每一章，并不是完全无关的概念。

比如，很多情况下对称性也是相似的一种。

比如，我们可能把相似的东西称为，这不是一样吗，也可能把等价的东西称为，这不是一样的吗。

比如，元其实就是二阶，也是一种自我指涉。