http://sigma425.hatenablog.com/entry/2014/12/07/132702
http://www.cppblog.com/sdfond/archive/2010/02/06/107364.html
http://en.wikipedia.org/wiki/Nim
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap.
Variants of Nim have been played since ancient times.[1] The game is said to have originated in China—it closely resembles the Chinese game of "Tsyan-shizi", or "picking stones"[2]—but the origin is uncertain; the earliest European references to Nim are from the beginning of the 16th century. Its current name was coined by Charles L. Bouton of Harvard University, who also developed the complete theory of the game in 1901,[3] but the origins of the name were never fully explained. The name is probably derived from German nimm meaning "take [imperative]", or the obsolete English verb nim of the same meaning.[4]
Nim can be played as a misère game, in which the player to take the last object loses. Nim can also be played as a normal play game, which means that the person who makes the last move (i.e., who takes the last object) wins. This is called normal play because most games follow this convention, even though Nim usually does not.
Normal play Nim (or more precisely the system of nimbers) is fundamental to the Sprague–Grundy theorem, which essentially says that in normal play every impartial game is equivalent to a Nim heap that yields the same outcome when played in parallel with other normal play impartial games (see disjunctive sum).
While all normal play impartial games can be assigned a nim value, that is not the case under the misère convention. Only tame games can be played using the same strategy as misère nim.
A version of Nim is played—and has symbolic importance—in the French New Wave film Last Year at Marienbad (1961).[5]
At the 1940 New York World's Fair Westinghouse displayed a machine, the Nimatron, that played Nim.[6] It was also one of the first ever electronic computerized games (1952). Herbert Koppel, Eugene Grant and Howard Bailer, engineers from the W.L. Maxon Corporation, developed a machine weighing 50 pounds which played Nim against a human opponent and regularly won.[7] A NIM Playing Machine has been described made from TinkerToy [8]
Nim is a special case of a poset game where the poset consists of disjoint chains (the heaps).
Game play and illustration[edit]
The normal game is between two players and played with three heaps of any number of objects. The two players alternate taking any number of objects from any single one of the heaps. The goal is to be the last to take an object. In misère play, the goal is instead to ensure that the opponent is forced to take the last remaining object.
The following example game is played between fictional players Bob and Alice who start with heaps of three, four and five objects.
Sizes of heaps Moves
A B C
3 4 5 Bob takes 2 from A
1 4 5 Alice takes 3 from C
1 4 2 Bob takes 1 from B
1 3 2 Alice takes 1 from B
1 2 2 Bob takes entire A heap, leaving two 2s.
0 2 2 Alice takes 1 from B
0 1 2 Bob takes 1 from C leaving two 1s. (In misère play he would take 2 from C leaving (0, 1, 0).)
0 1 1 Alice takes 1 from B
0 0 1 Bob takes entire C heap and wins.
Mathematical theory[edit]
Nim has been mathematically solved for any number of initial heaps and objects, and there is an easily calculated way to determine which player will win and what winning moves are open to that player. In a game that starts with heaps of three, four, and five, the first player will win with optimal play, whether the misère or normal play convention is followed.
The key to the theory of the game is the binary digital sum of the heap sizes, that is, the sum (in binary) neglecting all carries from one digit to another. This operation is also known as "exclusive or" (xor) or "vector addition over GF(2)". Within combinatorial game theory it is usually called the nim-sum, as it will be called here. The nim-sum of x and y is written x ⊕ y to distinguish it from the ordinary sum, x + y. An example of the calculation with heaps of size 3, 4, and 5 is as follows:
Binary Decimal
0112 310 Heap A
1002 410 Heap B
1012 510 Heap C
---
0102 210 The nim-sum of heaps A, B, and C, 3 ⊕ 4 ⊕ 5 = 2
An equivalent procedure, which is often easier to perform mentally, is to express the heap sizes as sums of distinct powers of 2, cancel pairs of equal powers, and then add what's left:
3 = 0 + 2 + 1 = 2 1 Heap A
4 = 4 + 0 + 0 = 4 Heap B
5 = 4 + 0 + 1 = 4 1 Heap C
---
2 = 2 What's left after canceling 1s and 4s
In normal play, the winning strategy is to finish every move with a Nim-sum of 0. This is always possible if the Nim-sum is not zero before the move. If the Nim-sum is zero, then the next player will lose if the other player does not make a mistake. To find out which move to make, let X be the Nim-sum of all the heap sizes. Take the Nim-sum of each of the heap sizes with X, and find a heap whose size decreases. The winning strategy is to play in such a heap, reducing that heap to the Nim-sum of its original size with X. In the example above, taking the Nim-sum of the sizes is X = 3 ⊕ 4 ⊕ 5 = 2. The Nim-sums of the heap sizes A=3, B=4, and C=5 with X=2 are
-
A ⊕ X = 3 ⊕ 2 = 1 [Since (011) ⊕ (010) = 001 ]
-
B ⊕ X = 4 ⊕ 2 = 6
-
C ⊕ X = 5 ⊕ 2 = 7
The only heap that is reduced is heap A, so the winning move is to reduce the size of heap A to 1 (by removing two objects).
As a particular simple case, if there are only two heaps left, the strategy is to reduce the number of objects in the bigger heap to make the heaps equal. After that, no matter what move your opponent makes, you can make the same move on the other heap, guaranteeing that you take the last object.
When played as a misère game, Nim strategy is different only when the normal play move would leave no heap of size two or larger. In that case, the correct move is to leave an odd number of heaps of size one (in normal play, the correct move would be to leave an even number of such heaps).
In a misère game with heaps of sizes three, four and five, the strategy would be applied like this:
A B C Nim-sum
3 4 5 0102=210 I take 2 from A, leaving a sum of 000, so I will win.
1 4 5 0002=010 You take 2 from C
1 4 3 1102=610 I take 2 from B
1 2 3 0002=010 You take 1 from C
1 2 2 0012=110 I take 1 from A
0 2 2 0002=010 You take 1 from C
0 2 1 0112=310 The normal play strategy would be to take 1 from B, leaving an even number (2)
heaps of size 1. For misère play, I take the entire B heap, to leave an odd
number (1) of heaps of size 1.
0 0 1 0012=110 You take 1 from C, and lose.
The previous strategy for a misère game can be easily implemented (for example in Python, below).
def nim(heaps, misere=True):
"""Computes next move for Nim in a normal or misère (default) game, returns tuple (chosen_heap, nb_remove)"""
X = reduce(lambda x,y: x^y, heaps)
if X == 0: # Will lose unless all non-empty heaps have size one
if max(heaps) > 1:
print "You will lose :("
for i, heap in enumerate(heaps):
if heap > 0: # Empty any (non-empty) heap
chosen_heap, nb_remove = i, heap
break
else:
sums = [t^X < t for t in heaps]
chosen_heap = sums.index(True)
nb_remove = heaps[chosen_heap] - (heaps[chosen_heap]^X)
heaps_twomore = 0
for i, heap in enumerate(heaps):
n = heap-nb_remove if chosen_heap == i else heap
if n>1: heaps_twomore += 1
# If move leaves no heap of size 2 or larger, leave an odd (misère) or even (normal) number of heaps of size 1
if heaps_twomore == 0:
chosen_heap = heaps.index(max(heaps))
heaps_one = sum(t==1 for t in heaps)
# misère (resp. normal) strategy: if it is even (resp. odd) make it odd (resp. even), else do not change
nb_remove = heaps[chosen_heap]-1 if heaps_one%2!=misere else heaps[chosen_heap]
return chosen_heap, nb_remove
Proof of the winning formula[edit]
The soundness of the optimal strategy described above was demonstrated by C. Bouton.
Theorem. In a normal Nim game, the player making the first move has a winning strategy if and only if the nim-sum of the sizes of the heaps is nonzero. Otherwise, the second player has a winning strategy.
Proof: Notice that the nim-sum (⊕) obeys the usual associative and commutative laws of addition (+) and also satisfies an additional property, x ⊕ x = 0 (technically speaking, that the nonnegative integers under ⊕ form an Abelian group of exponent 2).
Let x1, ..., xn be the sizes of the heaps before a move, and y1, ..., yn the corresponding sizes after a move. Let s = x1 ⊕ ... ⊕ xn and t = y1 ⊕ ... ⊕ yn. If the move was in heap k, we have xi = yi for all i ≠ k, and xk > yk. By the properties of ⊕ mentioned above, we have
t = 0 ⊕ t
= s ⊕ s ⊕ t
= s ⊕ (x1 ⊕ ... ⊕ xn) ⊕ (y1 ⊕ ... ⊕ yn)
= s ⊕ (x1 ⊕ y1) ⊕ ... ⊕ (xn ⊕ yn)
= s ⊕ 0 ⊕ ... ⊕ 0 ⊕ (xk ⊕ yk) ⊕ 0 ⊕ ... ⊕ 0
= s ⊕ xk ⊕ yk
(*) t = s ⊕ xk ⊕ yk.
The theorem follows by induction on the length of the game from these two lemmas.
Lemma 1. If s = 0, then t ≠ 0 no matter what move is made.
Proof: If there is no possible move, then the lemma is vacuously true (and the first player loses the normal play game by definition). Otherwise, any move in heap k will produce t = xk ⊕ ykfrom (*). This number is nonzero, since xk ≠ yk.
Lemma 2. If s ≠ 0, it is possible to make a move so that t = 0.
Proof: Let d be the position of the leftmost (most significant) nonzero bit in the binary representation of s, and choose k such that the dth bit of xk is also nonzero. (Such a k must exist, since otherwise the dth bit of s would be 0.) Then letting yk = s ⊕ xk, we claim that yk < xk: all bits to the left of d are the same in xk and yk, bit d decreases from 1 to 0 (decreasing the value by 2d), and any change in the remaining bits will amount to at most 2d−1. The first player can thus make a move by taking xk − yk objects from heap k, then
t = s ⊕ xk ⊕ yk (by (*))
= s ⊕ xk ⊕ (s ⊕ xk)
= 0.
The modification for misère play is demonstrated by noting that the modification first arises in a position that has only one heap of size 2 or more. Notice that in such a position s ≠ 0, therefore this situation has to arise when it is the turn of the player following the winning strategy. The normal play strategy is for the player to reduce this to size 0 or 1, leaving an even number of heaps with size 1, and the misère strategy is to do the opposite. From that point on, all moves are forced.
Other variations of Nim[edit]
Dividing natural number[edit]
Give any natural number n, the two people can divide n by a prime power ( A000961) which is a factor of n, the person who get 1 wins.
A000961) which is a factor of n, the person who get 1 wins.
If n = 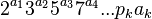 , where
, where 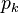 is the k-th prime, then it is a nim game with k groups of stones, and the r-th groups has
is the k-th prime, then it is a nim game with k groups of stones, and the r-th groups has  stones.
stones.
If the divisor changes to "can be a power of squarefree numbers" (sequence A072774 in OEIS), it is Wythoff's game.
The subtraction game S(1,2,...,k)[edit]
In another game which is commonly known as Nim (but is better called the subtraction game S (1,2,...,k)), an upper bound is imposed on the number of objects that can be removed in a turn. Instead of removing arbitrarily many objects, a player can only remove 1 or 2 or ... or k at a time. This game is commonly played in practice with only one heap (for instance with k = 3 in the game Thai 21 on Survivor: Thailand, where it appeared as an Immunity Challenge).
Bouton's analysis carries over easily to the general multiple-heap version of this game. The only difference is that as a first step, before computing the Nim-sums, we must reduce the sizes of the heaps modulo k + 1. If this makes all the heaps of size zero (in misère play), the winning move is to take k objects from one of the heaps. In particular, in ideal play from a single heap of nobjects, the second player can win if and only if
-
n ≡ 0 (mod
k+1) (in normal play), or
-
n ≡ 1 (mod
k+1) (in misère play).
This follows from calculating the nim-sequence of S(1,2,...,k),
-

from which the strategy above follows by the Sprague–Grundy theorem.
The 21 game[edit]
The game "21" is played as a misère game with any number of players who take turns saying a number. The first player says "1" and each player in turn increases the number by 1, 2, or 3, but may not exceed 21; the player forced to say "21" loses. This can be modeled as a subtraction game with a heap of 21–n objects. The winning strategy for the two-player version of this game is to always say a multiple of 4; it is then guaranteed that the other player will ultimately have to say 21 – so in the standard version where the first player opens with "1", they start with a losing move.
The 21 game can also be played with different numbers, like "Add at most 5; lose on 34".
A sample game of 21 in which the second player follows the winning strategy:
Player Number
1 1
2 4
1 5, 6 or 7
2 8
1 9, 10 or 11
2 12
1 13, 14 or 15
2 16
1 17, 18 or 19
2 20
1 21
The 100 game[edit]
A similar version is the "100 game": two players start from 0 and alternatively add a number from 1 to 10 to the sum. The player who reaches 100 wins. The winning strategy is to reach a number in which the digits are subsequent (e.g. 01, 12, 23, 34,...) and control the game by jumping through all the numbers of this sequence. Once reached 89, the opponent has lost (he can only tell numbers from 90 to 99, and the next answer can in any case be 100).
A multiple-heap rule[edit]
In another variation of Nim, besides removing any number of objects from a single heap, one is permitted to remove the same number of objects from each heap.
Circular Nim[edit]
Yet another variation of Nim is 'Circular Nim', where any number of objects are placed in a circle, and two players alternately remove one, two or three adjacent objects. For example, starting with a circle of ten objects,
. . . . . . . . . .
three objects are taken in the first move
_ . . . . . . . _ _
then another three
_ . _ _ _ . . . _ _
then one
_ . _ _ _ . . _ _ _
but then three objects cannot be taken out in one move.
Grundy's game[edit]
In Grundy's game, another variation of Nim, a number of objects are placed in an initial heap, and two players alternately divide a heap into two nonempty heaps of different sizes. Thus, six objects may be divided into piles of 5+1 or 4+2, but not 3+3. Grundy's game can be played as either misère or normal play.
Greedy Nim[edit]
See Greedy Nim.
Index-k Nim[edit]
A generalization of multi-heap Nim was called "Nim " or "index-k Nim by E. H. Moore,[9] who analyzed it in 1910. In index-k Nim, instead of removing objects from only one heap, players can remove objects from at least one but up to k different heaps. The number of elements that may be removed from each heap may be either arbitrary, or limited to at most r elements, like in the "subtraction game" above.
" or "index-k Nim by E. H. Moore,[9] who analyzed it in 1910. In index-k Nim, instead of removing objects from only one heap, players can remove objects from at least one but up to k different heaps. The number of elements that may be removed from each heap may be either arbitrary, or limited to at most r elements, like in the "subtraction game" above.
The winning strategy is as follows: Like in ordinary multi-heap Nim, one considers the binary representation of the heap sizes (or heap sizes modulo 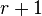 ). In ordinary Nim one forms the XOR-sum (or sum modulo 2) of each binary digit, and the winning strategy is to make each XOR sum zero. In the generalization to index-k Nim, one forms the sum of each binary digit modulo
). In ordinary Nim one forms the XOR-sum (or sum modulo 2) of each binary digit, and the winning strategy is to make each XOR sum zero. In the generalization to index-k Nim, one forms the sum of each binary digit modulo 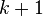 .
.
Again the winning strategy is to move such that this sum is zero for every digit. Indeed, the value thus computed is zero for the final position, and given a configuration of heaps for which this value is zero, any change of at most k heaps will make the value non-zero. Conversely, given a configuration with non-zero value, one can always take from at most k heaps, carefully chosen, so that the value will become zero.
【概述】
最近的几次比赛,博弈的题目一直不少,而且博弈问题是一块比较复杂、庞大的内容,因此在这里小结一下,希望能够帮自己理清一些思路,争取也多来几个系列,呵呵。
竞赛中出现的组合游戏问题一般都满足以下特征:
1. 二人博弈游戏,每个人都采用对自己最有利的策略,并且是两个人轮流做出决策
2. 在游戏中的任意时刻,每个玩家可选择的状态是固定的,没有随机成分
3. 游戏在有限步数内结束,没有平局出现
大部分的题目都满足上述条件,因此这里只讨论在上述条件范畴内的博弈问题。这类博弈问题,通常还有若干分类。一种是规定移动最后一步的游戏者获胜,这种规则叫做
Normal Play Rule
;另一种是规定移动最后一步的游戏者输,这种规则叫做
Misere Play Rule
,也称为Anti-SG游戏。此外,对于游戏的双方,如果二者博弈的规则相同,那么称为这类游戏是
对等
(impartial games)的;否则称为
不平等游戏
(partizan games )。当初WHU的那场比赛就是由于对于这个概念不是很清晰,导致看完题目之后就用SG定理来做,浪费了很多机时。实际上,解决不平等博弈问题的方法和普通的博弈问题(SG游戏)是有区别的,一般会采用动态规划或者surreal number。
【博弈基础知识】
在SG游戏中,最为人熟知的是必胜必败态,也叫NP态理论。注意的是,P态对应的是先手必败态,N态对应的是先手必胜态。必胜必败态理论是:
1. All terminal positions are P-positions
2. From every N-position, there is at least one move to a P-position
3. From every P-position, every move is to an N-position
英文的表述非常简洁清晰,而且这个理论也很好理解,如果在当前状态的下一步可以走到必败态,那么当前玩家就可以走到那个状态,把必败态推给另一方;如果所有可达状态都是必胜态,那么当前玩家无论如何走,都会把必胜态让给对方。根据必胜必败态理论,我们可以递归的求出每个状态是N态还是P态。必胜必败态理论其实已经把博弈问题转化成了一个有向图,借助图这个模型来分析问题,使得问题变得形象了许多。需要注意的是,这种SG游戏对应的有向图是无环的,因为如果有环,那么游戏双方就可能在环上不停的转换状态,游戏不能在有限步终止,这样就不满足组合游戏的特征3了。
然而在很多时候仅仅知道某个状态是必胜还是必败是不够的,因为如果存在多个组合游戏(比如经典的Nim),对应的状态集合非常大,无法直接利用必胜必败态理论求解,因此需要用到博弈论中一个很重要的工具:SG函数。
某个状态的SG函数值定义为当前状态所有不可达的状态编号中最小的编号,其中终止态的SG函数值是0。有了这个工具,就引入一个非常强大的定理——SG分解定理:
多个组合游戏的SG函数值是每个组合游戏的函数值的和。
(这里的和定义为异或操作)
SG分解定理的证明不是很难,其实和Nim的证明很像。根据这个定理,我们就知道为什么Nim的解法是异或所有的石子个数了,因为每堆石子的SG值就是石子的个数。SG分解定理告诉我们任何SG游戏都可以转化成Nim游戏来做。
Nim中的一个变形就是拿走最后一块石子的人算输。通过修改SG的计算规则,可以得出相同的结论(因为当石子个数是1的时候SG值为0,因此要单独处理);当然也可以利用一个叫做SJ定理的方法来做,依然是要处理当所有堆的SG值不大于1的情况。
【博弈基本模型】
除了Nim模型,很多模型都看似复杂,最后都划归到了Nim模型上,然后利用SG分解来做的。在证明两种模型等价的时候,可以通过计算SG值判断是否相同,或者通过判断必胜策略的走法将其转化为Nim。许多模型非常的神奇,其获胜策略又千差万别,因此无法一一列举,但是掌握一些经典模型是必须的,这样通过模型的转化可以简化问题的难度。
经典模型1:Nim变种。
包括:
(1) 楼梯Nim。把奇数台阶的石子作为Nim,二者等价,因为必胜的策略是相同的。
(2) 每次可以取k堆,这个是经典的Moore Nim。它是泛化的Nim游戏。
(3) 两堆石子,每次可以取一堆或两堆,从两堆取得时候个数必须相同,谁先取完获胜。这个是著名的威佐夫博弈,跟黄金分割数有关,具体证明不是很清楚,但是用SG值打表可以找出规律。代码如下:
#include
<
cstdio
>
#include
<
cmath
>
#include
<
algorithm
>
using
namespace
std;
int
main()
{
const
double
k
=
(sqrt(
5.0
)
+
1
)
/
2.0
;
int
a, b, t;
while
(scanf(
"
%d %d
"
,
&
a,
&
b)
==
2
)
{
if
(a
>
b)
swap(a, b);
t
=
b
-
a;
if
(a
==
(
int
)(t
*
k))
puts(
"
0
"
);
else
puts(
"
1
"
);
}
return
0
;
}
(4) Subtraction Games。一种通用的Nim游戏,每次从可用状态集合中选择下一步的状态,有很多变形,核心思想还是计算SG函数值。
(5) Take-and-Break Game。每次把局面分成多个Nim子游戏,利用SG分解定理求出对应的SG值。
经典模型2:翻硬币游戏(Coin Turning Game)
(1) 一维的翻硬币游戏,每次可以翻1个或两个。通过单独考虑每个可以翻的硬币发现,Coin Turning Game的SG值和Nim等价,因此两个模型等价。需要注意的是,许多翻硬币游戏根据题目的要求,一般编号从0开始。
(2) 一维的翻硬币游戏,每次可以翻1个或两个,限定了翻第二枚硬币的范围,那么就和Subtraction Game等价了。
(3) 一维的翻硬币游戏,每次可以翻1个、2个或3个,这个游戏叫做Mock Turtles,有一个神奇的规律,是Odious Number序列。
(4) 高维的翻硬币游戏,需要用到Nim积和Tartan定理。
翻硬币模型的变化更多,很多模型都有一些奇妙的规律,需要打表才能发现。
经典模型3:删边游戏(Green Hackenbush)
(1) 树的删边游戏:Colon原理证明这种模型和Nim依然是等价的,多个叉的SG值异或就是对应根节点的SG值。
(2) 无向图删边游戏:利用Fursion定理收缩圈,然后就转换成树的删边游戏了,不过这个定理还不会证。
注:本文作于2009年8月3日 09点33分
Misere(正しくはMisère) Game とは,(多分)"最後の一個をとったら負け"みたいなゲームの事で,例えばNimに対して Misere Nimというものが考えられる.
Nimの勝利条件がNimber(Grundy number)であることはwell known factだが,Misere Nimの勝利条件を知らなかったのでメモ.(2014年12月放送の頭脳王という番組に番組独自の問題として出てきた,後述)
実はNimとほとんど同じで基本的に相手にxorが0の状態を渡せばいいのだが,最後までそれをやるとこっちが負けるので,最後はちょっと変える.正確には,その状態で次に動かすプレイヤーの敗北条件は,
{ if ∃i,xi>1 otherwise ⨁n−1i=0xi=0⨁n−1i=0xi=1
となる.
prf(の概略).
後半は自明(残り奇数個なら最後取ってしまうので).
前半はNimと一緒で,あとは前半から後半にうまく移行できるかだが,全て1以下の状態でこっちに帰ってくることがないようにすれば良い.
普通のNimっぽくやって自分に1,..,1(2k-1個(k>=1))が来るような手になった時どう改善すればよいか考える.
その直前の相手の状態は,"1が2k個"または"1が2k-2個,xが1個(x>1)"(以下x>1とする)だが,後者はありえない(xorが0にならないので).
よって更にその直前の自分の状態を考えると,
この時はこの段階で対処をすべき(ちゃんというと,帰納法で示される(前半から後半へ移行出来る状態では必ず対処できる段階があるため)).
xを全て取る
よって必敗を相手に回せることがわかった.
それ以外で負けることは,それ以外の状態で以上の状態のどれかに引き渡せることが(Nim同様に)わかるため言える.■
なんでこの記事を書こうと思ったかというと,2014年12月放送の頭脳王という番組で,番組独自のゲームとしてpileが3個のmisere Nimを出場者にやらせていて(vs コンピュータ),まあそれはまだ百歩譲って許せなくはないのだが,しかも数十手先を見通す力とか的はずれなことを言っていたが(石は数十個もない)(まあいつもの煽りだから許される).許されないのは,それぞれの人に初期状態として別の手が渡されていたのだが,
そのうちいくつかは必敗でいくつかは必勝だったという激ヤバな事実があったからです(先手で(3,9,10)が渡された人と(4,5,9)が渡された人がいた).
しかもコンピュータ側の動きを見ると,ちゃんと必勝の手に従っていたので,多分わざとだと思う.(一応コンピュータは探索をしているだけで,必勝かどうかは出題側は知らなかった(独自のゲームとして紹介しているので)と言い張ることは可能だけれど)
必敗の人かわいそうだった.
50点問題で,その時点での点数が150,110,100,60で2位以上勝ち抜けだったので同点を避けたのかなあ.
追記:
genkiさんのコメントの通り,"この状態は必敗である"という主張ができたら流石にOK(つまり点数を得られる)と思われるので,(当然ゲーム的には必敗だが,)"参加者は"完全"に勝ちの目を閉ざされた"というのは言いすぎだという注釈をつけておきます.










 本文探讨了Nim游戏的Misere规则及其胜利条件,解释了如何通过异或运算来判断必败状态,并提供了关键的策略指导。通过实例分析,揭示了在Misere游戏中如何将状态转化为必胜态,确保最终胜利。
本文探讨了Nim游戏的Misere规则及其胜利条件,解释了如何通过异或运算来判断必败状态,并提供了关键的策略指导。通过实例分析,揭示了在Misere游戏中如何将状态转化为必胜态,确保最终胜利。
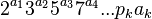 , where
, where 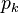 is the k-th prime, then it is a nim game with k groups of stones, and the r-th groups has
is the k-th prime, then it is a nim game with k groups of stones, and the r-th groups has  stones.
stones.
 " or "index-k Nim by E. H. Moore,
" or "index-k Nim by E. H. Moore,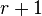 ). In ordinary Nim one forms the XOR-sum (or sum modulo 2) of each binary digit, and the winning strategy is to make each XOR sum zero. In the generalization to index-k Nim, one forms the sum of each binary digit modulo
). In ordinary Nim one forms the XOR-sum (or sum modulo 2) of each binary digit, and the winning strategy is to make each XOR sum zero. In the generalization to index-k Nim, one forms the sum of each binary digit modulo 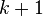 .
.
















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








