【算法设计与分析】动态规划算法（矩阵连乘问题、0-1背包问题、最长公共子序列问题、最优二叉检索树问题）

实验目的

1）了解动态规划算法思想；
2）掌握算法的基本要素及解题步骤；
3）能够对实际问题，能够按照动态规划解题步骤，分析问题；
4）能够正确的编码、实现动态规划算法；
5）能够正确分析算法的时间复杂度和空间复杂度。

实验环境

VC6.0 / Eclipse / Pycharm。

实验内容

矩阵连乘问题

<1>实验内容（要求）；

已知矩阵A1 A2 A3 A4 A5 ，使用向量P<P0=3，P1=2，P2=5，P3=10，P4=2，P5=3>存储行列，求出相乘次数最少的加括号位置。

<2>算法设计(问题分析、建模、算法描述)；

一些矩阵乘法中的性质：

1. 若矩阵A 为 p × q ，矩阵B 为 q × r ，则A × B 的代价为p * q * r；
2. 当i=j时，A[i,j]=Ai, m[i,j]=0;(表示只有一个矩阵,如A1,没有和其他矩阵相乘,故乘的次数为0)；
3. 当i<j时，m[i,j]=min{ m[i, k] + m[k + 1, j] + pi - 1 * pk * pj } ,其中 i <= k < j ；

<3>算法源码；

输入格式：
第一行 一个正整数 n 表示矩阵的个数。
第二行 输入n + 1 个数，相邻两个数分别代表矩阵的行、列数。

#include<iostream>
using namespace std;
const int N = 100;
int A[N];//矩阵规模
int m[N][N];//最优解
int s[N][N];
void MatrixChain(int n)
{
    int r, i, j, k;
    for (i = 0; i <= n; i++)//初始化对角线
    {
        m[i][i] = 0;
    }
    for (r = 2; r <= n; r++)//r个矩阵连乘
    {
        for (i = 1; i <= n - r + 1; i++)//r个矩阵的r-1个空隙中依次测试最优点
        {
            j = i + r - 1;
            m[i][j] = m[i][i]+m[i + 1][j] + A[i - 1] * A[i] * A[j];
            s[i][j] = i;
            for (k = i + 1; k < j; k++)//变换分隔位置，逐一测试
            {
                int t = m[i][k] + m[k + 1][j] + A[i - 1] * A[k] * A[j];
                if (t < m[i][j])//如果变换后的位置更优，则替换原来的分隔方法。
                {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
    }
}
void print(int i, int j)
{
    if (i == j)
    {
        cout << "A[" << i << "]";
        return;
    }
    cout << "(";
    print(i, s[i][j]);
    print(s[i][j] + 1, j);//递归1到s[1][j]
    cout << ")";
}
int main()
{
    int n;//n个矩阵
    cin >> n;
    int i, j;
    for (i = 0; i <= n; i++)
    {
        cin >> A[i];
    }
    MatrixChain(n);
    cout << "最佳添加括号的方式为：";
    print(1, n);
    cout << "\n最小计算量的值为：" << m[1][n] << endl;
    return 0;
}

<4>测试数据及运算结果(要求：截图说明算法运行的结果)；

输入：
5
3 2 5 10 2 3

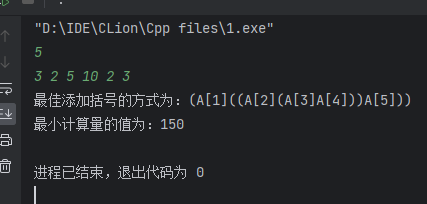
输出：
最佳添加括号的方式为：(A1)
最小计算量的值为：150

<5>算法分析(分析算法的时间复杂度和空间复杂度)。

时间复杂度：O（n³）
空间复杂度：O（n²）

0-1背包问题

<1>实验内容（要求）；

有5个物品，其重量分别为{2,2,6,5,4}，价值分别为{6,3,5,4,6}。背包容量为10，物品不可分割，求装入背包的物品和获得的最大价值。

<2>算法设计(问题分析、建模、算法描述)；

1. 状态f[ i ][ j ]定义：前 i 个物品，背包容量 j 下的最优解（最大价值）
   当前的状态依赖于之前的状态，可以理解为从初始状态f[0][0] = 0开始决策，有 N件物品，则需要 N 次决 策，每一次对第 i 件物品的决策，状态f[ i ][ j ]不断由之前的状态更新而来。
2. 当前背包容量不够（j < v[i]），没得选，因此前 i 个物品最优解即为前 i − 1 个物品最优解
   对应代码：f [ i ][ j ] = f [i - 1][ j ]。
3. 当前背包容量够，可以选，因此需要决策选与不选第 i 个物品
   • 选：f [ i ][ j ] = f [i - 1][j - v[ i ]] + w[ i ]
   • 不选：f [ i ][ j ] = f[i - 1][ j ]
   • 我们的决策是如何取到最大价值，因此以上两种情况取 max()

<3>算法源码；

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1005;
int v[MAXN];    // 体积
int w[MAXN];    // 价值 
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;

    return 0;
}

<4>测试数据及运算结果(要求：截图说明算法运行的结果)；

输入：
5 10
2 6
2 3
6 5
5 4
4 6

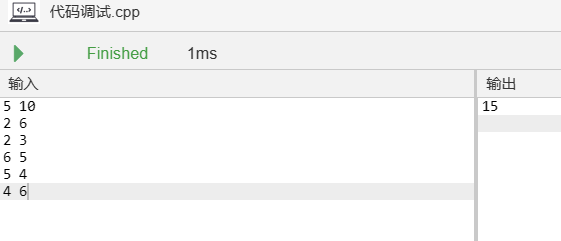
输出：
15

<5>算法分析(分析算法的时间复杂度和空间复杂度)。

• 时间空间复杂度均为O（n * m）

最长公共子序列问题

<1>实验内容（要求）；

求X={A,B,C,B,D,A,B}和Y={B,D,C,A,B,A}的最长公共子序列。

<2>算法设计(问题分析、建模、算法描述)；

1. 经典LCS，如果暴力时间就会到O（n³）直接爆掉，做法应该是动态规划来写
2. 通过dp来确定哪些字符是最长公共子序列中的字符，mat[i][j] 表示第一个序列的前 i 个字符和第二个序列的前 j 个字符的公共子序列
3. 每次转移有三个状态做出抉择：
   （1）第一种状态不录入第一个序列的第i个字符时的最长公共子序列，
   （2）第二种状态不录入第二个序列的第j个字符时的最长公共子序列，
   （3）第三种状态第一个序列的前 i - 1 个字符与第二个序列前 j - 1 个字符的公共子序列加上最后一个字符的录入状态，如果最后的一个字符相等则录入状态为1，否则为0。
4. 状态转移方程：
   dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j -1 ],dp[ i - 1 ][ j - 1 ] + (A[ i ] == B[ j ] ? 1 : 0))

<3>算法源码；

#include<bits/stdc++.h>

using namespace std;

char a[1001], b[1001];  // 定义两个字符串a和b，长度为1001
int dp[1001][1001], len1, len2;  // 定义二维数组dp和长度为1001的整型变量len1、len2

void lcs(int i, int j)  // 定义函数lcs，参数为整型变量i和j
{
    for (i = 1; i <= len1; i++) 
    {
        for (j = 1; j <= len2; j++)
        {
            if (a[i - 1] == b[j - 1])  // 如果a[i-1]等于b[j-1]
                dp[i][j] = dp[i - 1][j - 1] + 1;  // dp[i][j]等于dp[i-1][j-1]+1
            else if (dp[i - 1][j] > dp[i][j - 1])  // 否则如果dp[i-1][j]大于dp[i][j-1]
                dp[i][j] = dp[i - 1][j];  // dp[i][j]等于dp[i-1][j]
            else  
                dp[i][j] = dp[i][j - 1];  // dp[i][j]等于dp[i][j-1]
        }
    }
}

void llcs()  // 定义函数llcs()
{
    int i, j, z = 0;  // 定义整型变量i、j和z，并将z初始化为0
    char c[1001];  // 定义字符数组c
    memset(c, 0, sizeof(c));  // 将c数组初始化为全0
    i = len1; 
    j = len2; 
    while(i != 0 && j != 0)  // 当i不等于0且j不等于0时循环
    {
        if (a[i - 1] == b[j - 1])  // 如果a[i-1]等于b[j-1]
        {
            c[z++] = a[--i];  // 将a[i-1]赋值给c[z++]，然后将i减1
            j--; 
        } else if (dp[i - 1][j] < dp[i][j - 1])  // 否则如果dp[i-1][j]小于dp[i][j-1]
            j--; 
        else if (dp[i][j - 1] <= dp[i - 1][j])  // 否则如果dp[i][j-1]小于等于dp[i-1][j]
            i--; 
    }
    for (i = z - 1; i >= 0; i--)  // 从z-1到0的逆序循环
        printf("%c", c[i]); 
    printf("\n"); 
}

int main()
{
    cin >> a; 
    cin >> b;
    memset(dp, 0, sizeof(dp)); 
    len1 = strlen(a); 
    len2 = strlen(b); 
    lcs(len1, len2); 
    llcs();  
    return 0;  
}

<4>测试数据及运算结果(要求：截图说明算法运行的结果)；

输入：
abcbdab
bdcaba

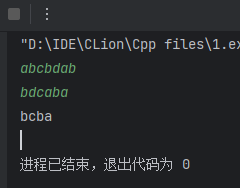
输出：
bcba

<5>算法分析(分析算法的时间复杂度和空间复杂度)

时间复杂度和空间复杂度均为 O(n * m)

最优二叉检索树问题（选做）

<1>实验内容（要求）；

求结点S[1,5] = {A,B,C,D,E}，概率分别为P = {0.04,0.1,0.02,0.3,0.02,0.1,0.05,0.2, 0.06,0.1,0.01}的最优二叉检索树。

<2>算法设计(问题分析、建模、算法描述)；

<3>算法源码；

<4>测试数据及运算结果(要求：截图说明算法运行的结果)；

<5>算法分析(分析算法的时间复杂度和空间复杂度)。