初识递归

最近做类的静态数据成员的题目碰到一道母牛生小牛，虽然这道题跟递归没什么关系，但是题目说不能用f(n)=f(n-1)+f(n-3)，我想了好久都想不明白怎么就f(n)=f(n-1)+f(n-3)了，之前虽然偶尔碰到过递归但是一直都没有系统地了解过，仔细想想我甚至都说不出什么是递归，那就借此机会好好理解一下递归，也算是提前预习一下数据结构和算法。

 

先看这道“母牛生小牛”——设有一头小母牛，从出生第四年起每年生一头小母牛，按此规律，第N年时有几头母牛？：

显然第N年的母牛要么本身就是之前的牛要么是之前的牛生的牛对吧，不会再突然加进来新的牛了，那这个肯定可以递推啊！

第一感觉 ==> 第N年的所有牛f() = 第N年新出生的牛fnew()和第N年不是新出生的牛fold() ==> f(N)=fold(N)+fnew(N)

如果能把fnew(N)和fold(N)都用f(N-?)即之前第?年的所有牛表示 ==> f(N)=f(N-?)+f(N-?) ==> 那么递推公式就出来了

第N年不是新出生的牛fold()显然就是去年的所有牛啊 ==> fold(N) = f(N-1)

第N年新出生的牛 <==> 第N年能生牛的牛生的牛 <==> 第N年4岁及4岁以上的牛 <==> 第N年>=4岁的牛

第N年>=4岁的牛能用之前某一年的所有牛f(?)表示吗，毕竟f(N)递推公式里的自变量肯定不能是N自己不然就死循环了

每一年的牛肯定都比之前任何一年的牛多，如果第N年>=4岁的牛可以往下展开成>=1岁的牛，那不就正好是那一年的所有牛了，那就可以用f(N-?)来表示fnew(N)了

第N年>=4岁的牛 <==> 第N-1年3岁和>=4岁的牛 <==> 第N-2年2岁3岁和>=4岁的牛 <==> 第N-3年1岁2岁3岁和>=4岁的牛

这个第N-3年1岁2岁3岁和>=4岁的牛不就是第N-3年的所有牛f(N-3)吗

为什么第N年新出生的牛正好是三年前的所有牛呢？==> 第N年新出生的牛=第N年能生小牛的牛 ==> 牛4岁的时候也就是出生的三年以后才能生小牛 ==> 今年的所有牛三年以后都满4岁了所以全部都能生小牛，明年的牛和后年的牛在第三年的时候都还有没满4岁的牛所以并不是全部都能生小牛 ==> 第N年新出生的牛就是三年前的所有牛 ==> fnew(N) = f(N-3)

∴ f(N) = fold(N) + fnew(N) <==> f(N) = f(N-1) + f(N-3) <==> 即第N年的所有牛=一年前的所有牛+三年前的所有牛

画个图验证一下好像确实没毛病：

 

 

接着是“约瑟夫环”——这道题出现过太多次了，从循环到链表到双链表再到异常处理，当时我考虑过递归但是确实写不来：

0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

由题意有两个变量需要我们给定数字总数n和删除间隔m，所以设：f(n,m)——总共有n个数字[0,n-1]且删除间隔为m的情况下留到最后的数字的下标

如果我们用固定队列进行删除：

第一次变化：f(n,m)——从n个数[0,n-1]中删除掉从头开始的第m个数然后把第m个数后面的数都向前移一位 ==> f(n-1,m)；

第二次变化：f(n-1,m)——从n-1个数[0,n-2]中删除掉从头开始的第m个数然后把第m个数后面的数都向前移一位 ==> f(n-2,m)；

但是这种情况删除间隔为1而不是m，要保证按间隔m循环删除，除非多添加一个数组参数记录每次删除后的位置并作为下一次删除的起始位置，但这好像也太麻烦了，那如果把f(n,m)改成f(n,m%n)，把第f(n-1,m)中二个参数m改成(m%n+m)%n <==> 2m%n，也就是f(n-1,2m%n)，这样第二次变化也可以以m的间隔进行删除了，所以f(n,m)应改为——f(n,(数字总个数-n+1)*m%n)；

易知此时f(n,m%n)与f(n-1,2m%n)有两种情况显然为：①f(n,m%n) = f(n-1,2m%n)   ②f(n,m%n) = f(n-1,2m%n) + 1

显然①≠②，这就有二义性没法实现了，所以固定队列的思路是行不通的。

那如果用循环队列进行删除：

第一次变化：f(n,m)——从n个数[0,n-1]中删除掉从头开始的第m个数然后把第m个数前面的数都移到第n个数后面 ==> f(n-1,m)；

第二次变化：f(n-1,m)——从n-1个数[0,n-2]中删除掉从头开始的第m个数然后把第m个数前面的数都移到第n-1个数后面 ==> f(n-2,m)；

使用循环队列就不需要记录每次删除的数的位置或者计算每次删除的位置的表达式了

如下图所示，f(n,m)删掉的数的下标是(m-1)%n，因为f(n,m)的值是n个数中最后留下的数的下标，所以这个下标永远都不会被删除；f(n-1,m)的值是n个数删掉一个数后剩下n-1个数的时候最后留下的数的下标；只要m不变无论n为多少这个最后留下的数一定都是同一个数，只是在循环队列中它的位置会随着n的变化而变化；我们去找f(n,m)和f(n-1,m)的关系就是把最后留下的数在f(n-1,m)中的下标还原成它原来在f(n,m)中的下标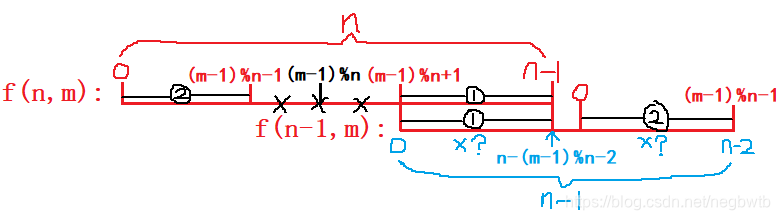

设f(n,m)=y，f(n-1,m)=x，因为y必在①、②中，所以x也必在①、②中

当x在①中时，y也必然在①中，(m-1)%n+1+x就是x还原后在上一个队列中的下标，即y=(m-1)%n+1+x<= n-1，显然y<=n-1没有越界，所以不用取余；

当x在②中时，y也必然在②中，依然有y=(m-1)%n+1+x，但此时y>n-1已越界，所以要取余即y=((m-1)%n+1+x)%n；

综上两种情况 ==> y=((m-1)%n+1+x)%n

继续化简 ==> y=((m-1)%n+(1+x)%n)%n //x最大值为n-2∴1+x=(1+x)%n

==> y=((m-1+1+x)%n)%n

==> y=(m-1+1+x)%n

==> y=(m+x)%n

==> f(n,m)=(m+f(n-1,m))%n

 

最后再看一道题：

一条包含字母 A-Z 的消息通过以下方式进行了编码：'A' -> 1，'B' -> 2，... ，'Z' -> 26
给定一个只包含数字的非空字符串，请计算解码方法的总数。

输入: "12" ==> 输出: 2 / 解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。

输入: "226" ==> 输出: 3 / 解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

设f(n)为非空字符串长度为n时解码方法的总数 

因为解码方法要求每个数字或者每两个数字都必须能解码成某个字母[1~26]，所以我们要用字母的取值情况来拆分数字

解码方法的总数f(n)即为n个数字能构成的所有字母组合的总数

设最后一个字母消耗数字的所有可能情况总数为k，g(x)为最后一个字母在第x种可能情况下消耗掉的数字的个数

f(n) = ∑(k,i=1)：f(n-g(i))

∵字母取值范围是[1,26]   ∴k=2   ∴g(x)∈(1,2)

设第一种情况为——最后一个字母消耗掉一个数字，此时g(i)=g(1)=1；

第二种情况只能为——最后一个字母消耗掉两个数字，此时g(i)=g(2)=2；

∴f(n) = ∑(k,i=1)：f(n-g(i)) = ∑(2,i=1)：f(n-g(i)) = f(n-g(1))+f(n-g(2)) = f(n-1)+f(n-2)

#include <iostream>
#include <string>
#include <vector>
using namespace std;
int decode(string intStr, int index, vector<int> &v){

    if(index<0){
        /*index<0表示——所有数字都消耗完，即所有的数字都以字母的形式入栈了
        说明已经确定了一个完整的字母序列，要将当前组合逆序输出(因为是倒序递归入栈)
        所以此时必须将栈顶字母弹出，不然没办法存放新的字母序列
        当确定了一个完整字母序列即为寻找到一种可能性，所以这里return给上一层的值是1*/
        for(vector<int>::const_reverse_iterator i = v.rbegin(); i != v.rend(); ++i)
            cout<<*i<<' ';
        cout<<endl;
        v.pop_back();
        return 1;
    }

    int count=0,temp;
    char curr=intStr[index];
    char prev=intStr[index-1];

    //字母的数字为1~26所以有两种情况：
    //①一个数字代表一个字母(curr范围：1~9即>0)
    //②两个数字代表一个字母(prev为1范围为：0~9 / prev为2：0~6)
    if(curr>'0'){
        temp=int(curr-48);
        /*调用递归说明已经确定了当前字母的取值(使用掉的数字)，即将递归计算剩下数字的字母组合
        递归就是不断缩小范围，逐渐确定每个字母取值的过程，每确定一个字母就递归进入下一层去确定下一个字母
        所以每次递归前都要将这个确定的字母入栈，每一层都有两个递归表示每个字母都有两种确定的方式*/
        v.push_back(temp);
        count=decode(intStr,index-1,v);//第①种情况将剩下index-1个数字继续递归
    }
    if(index>0 && (prev=='1' || (prev=='2'&&curr<='6'))){
        temp=int((prev-48)*10)+int(curr-48);
        v.push_back(temp);
        count+=decode(intStr,index-2,v);//第②种情况将剩下index-2个数字继续递归
    }

    /*当栈中字母未使用的数字的所有字母组合的可能性都计算完成后，需要将可能性的总数count进行return；
    若在计算未使用数字所有可能的字母组合时发现这些数字不能组成字母序列，
    说明当前栈中已确定的字母序列能组成的完整的字母序列(消耗完所有字母)的组合总数是0，
    这时需要弹出栈顶的字母，return count=0结束这个错误序列的递归，更新栈中序列后，重新递归计算新序列结果；
    上述两种return的情况都说明当前栈中已确定的字母序列已经不存在构成其他新完整序列的可能性，
    这个时候只能改变栈中已确定的字母序列继续去寻找新的完整序列，所以要将栈顶字母弹出*/
    v.pop_back();
    return count;
}
int numDecode(string intStr){
    vector<int> v;
    //要进行修改的全局变量一定传引用
    return decode(intStr, intStr.length()-1, v);
}
int main(){
    string s="12212";
    cout<<numDecode(s);
    return 0;
}

 

做完这三道题以后我又思考了一下递归的具体过程和它的适用性，我发现我每次想得很复杂但是一打断要么就忘了要么就乱了，我觉得如果有时间我应该尽量把我每一次思考的步骤、结果和递进的过程都记录下来，如果能经常回头看看我之前的思考有哪些漏洞哪里的联系不够紧密或者哪里不够简洁，把它们强化一下应该对提升我的思考速度和思考方式帮助挺大的。所以记录的时候应该尽量具体地还原这些想法产生的过程和它们之间的关系，不要觉得繁琐。

对于一个有规律的数列 an ，要对它的第k项进行递归求解的整个过程大致为：

如果an的每一项都可以表示为之前若干项的函数—— a[k] = f(a[k-x]) ? g(a[k-y]) ?......? h(a[k-z]) {x<y<z<k, ?为运算法则} 

而且我们又很容易知道这个数列前 z 项的值：a[1]、a[2]、... 、a[z]

那么对于第k项a[k]，就可以通过递归逐渐地缩小表达式中每一个自变量下标(k-x,k-y,...,k-z)的范围（因为x<y<z<k，不满足不可以递归），每一次递归都进一步缩小自变量下标的范围例如在a[k-x]的下一次递归中： a[k-x]= f(k-x-x) ? g(k-x-y) ?......? h(k-x-z)；在进行一定次数的递归后表达式中所有的未知项(包含k的项)都会被已知项(a[1]~a[z])代替，此时表达式中的每一个自变量下标的范围均∈[1,z]，可以看做a[k]表达式中的k已经被消去，a[k]的新表达式可以用已知项表示出来：ak = F(z) ?......? G(2) ? H(1)

这个过程也可以理解为一个线性的展开——对a[k]中的初始未知项：a[k-x]、a[k-y]、... 、a[k-z] 按照规则向下进行展开，然后对展开后的新表达式中的未知项依然按照规则继续向下展开；展开过程中子函数f()、g()、... 、h()的个数越来越多，但是函数中自变量的下标却越展开越小；直到最后整个表达式中所有函数的自变量都是已知项(即前z项)：a[1]、a[2]、... 、a[z] ；此时展开过程中的每一个未知项都变成了以已知项为自变量的新复合函数，这时没有必要再继续展开，直接带入已知项的值即可算出原a[k]表达式的结果

不难看出递归就是一个消去未知项(逐步将未知项用已知项表示)的过程，这让我回想起高中函数中最简单的一类送分填空题：

已知f(1)=1，f(2)=1，f(3)=1，f(n)=f(n-1) + f(n-3)，求f(7)
  f(7)
= f(6)   +   f(4)
= f(5)+f(3)   +   f(3)+f(1)
= f(4)+f(2)  +  f(3)   +   f(3)+f(1)
= f(3)+f(1) + f(2)  +  f(3)   +   f(3)+f(1)
= 1+1 + 1  +  1   +   1+1
= 6

这不就是用递归公式求第七年母牛的数量吗？仔细观察发现这种递归方程的求解步骤展开之后特别像一棵树，而且像是在先序创建一棵完全二叉树，求解步骤中等号代表着开始创建二叉树的下一层，每一个等号后面都包含了当前深度二叉树的全部叶子节点，停止创建这棵二叉树的条件(递归终止的条件)也就是方程停止展开的条件为：所有的叶子节点(=号后面的所有项)均为已知项，此时不再递归创建(方程不再继续分解)，直接返回所有叶子节点的和即为要求的第n项的值。

但是仔细观察递归的过程发现其实跟上面的求解f(n)的步骤并不一样，递归的特点是在展开一个未知项的时候如果还没有完全展开(所有项均为已知项)是不会进行另一个未知项的展开的，例如——a[k-x]在完全展开之前，是不会对a[k-y]、a[k-z]进行展开的；同理a[k-x]的下一层的首个子项a[k-x1]在完全展开之前也是不会去展开该层中的其他子项如：a[k-y1]、a[k-z1]。只有当a[k-x]的第n层的首子项a[k-xn]完全展开成已知项，将已知项带入计算出结果并返回给a[k-xn]以后，才会接着去进行与a[k-xn]同层的下一个子项的展开，即a[k-yn]的展开。最终在完成了a[k-x]所有层的展开并返回了计算得到的结果给a[k-x]以后，才会对a[k-y]、a[k-z]进行展开。

那如果f(n)不是向下展开而是向上展开比如f(n)=f(n+1)+f(n+3)，这个递归法则的自变量是在无限扩大的，这种情况还能进行递归计算吗？假设我们需要计算f(k)，n为我们可能需要计算的项数范围，即k∈[1,n]，有：f(n)=f(n+1)+f(n+3)、f(n-1)=f(n)+f(n+2)、f(n-2)=f(n-1)+f(n+1)、f(n-3)=f(n-2)+f(n)......可以发现只要我们给出f(n+1)、f(n+2)、f(n+3)三个连续的项的值就可以划定一个上界[1,n+3]，不超过该上界的所有项都可以用这仅包含这三个已知项的函数表示，此时递归的计算成为可能。

又如果f(n)是双向展开的呢？比如f(n)=f(n+x)+f(n-y)。易证f(n)的展开式中必定包含f(n)自己，所以该情况无法完成递归的计算。

综合以上情况，可以将最初的的表达式：a[k] = f(a[k-x]) ? g(a[k-y]) ?......? h(a[k-z]) {x<y<z<k, ?为运算法则} ，修改为：

a[k] = f(a[k-x]) ? g(a[k-y]) ?......? h(a[k-z]) {k>|z|>|x|>|y|且xyz同号，?为运算法则}

如果一个数列an的第k项可以被描述为上述情况，那么该数列是可以进行递归的，其过程如下——递归自顶向下先序创建一棵完全n叉树(n为递归法则中未知项项数)；需要我们给定的初始条件为前z项(a[1],a[2],...,a[z])的值；终止条件是——该节点的n个子节点全部为已知项(将每一个已知项都视为叶子节点，一旦某个节点的所有子节点都为叶子节点，就将这n个叶子节点的值按照递推公式进行运算后的结果返回给上一个父节点，此时已知父节点的值父节点为已知项即父节点变成了新的叶子节点[一开始只有初始条件为已知项])；递归向上回溯的过程是在后续遍历之前创建的完全n叉树，完成一个节点k的遍历过程是——将k节点的n个子叶子节点(非真叶子节点，只是已知项)带入递归公式计算出结果并将这个结果return给k节点，也视为完成了对k节点的递归调用。

还有很多时候a(k-x)的展开子项与a(k-y)和a(k-z)的展开子项会产生重复(最坏情况newO(n)=递推公式中未知项项数*oldO(n))，如果用数组a[n]保存第一次出现的每一个展开项(这个过程在自底向上的回溯中完成，实际上类似于循环——从最低层的已知项按照规则循环n次逐项推出下n项的值)，也就是在第k层用数组的第k项a[k]去接收自变量k调用递归的结果(即第k-1层return返回的值)，所以a(k-x)在递归中已经保存过的子项，a(k-y)与a(k-z)先用y和z作为下标取数组元素，如果不存在才会触发递归

总而言之对于满足如下通式且能确定下界值的数列，其递归函数的代码大致可以写成：

a[k] = f(a[k-x]) ? g(a[k-y]) ?......? h(a[k-z]) {k>|z|>|x|>|y|且xyz同号，?为运算法则}

​​​​​int recursion(int n, int &arr[]){
    if(n<=z)
        return arr[n];

    if(!arr[n-x])
        arr[n-x]=recursion(n-x,arr);
    if(!arr[n-y])
        arr[n-y]=recursion(n-y,arr);
    ......
    if(!arr[n-z])
        arr[n-z]=recursion(n-z,arr);

    arr[n] = f(arr[n-x]) ? g(arr[n-y]) ?......? h(arr[n-z]);
    return arr[n]
}
void test(){
    int n;
    cin>>n;

    int arr[n+1]={0};
    arr[1]=a;
    arr[2]=b;
    ......
    arr[z-1]=c;
    arr[z]=d;
    
    cout<<recursion(n,arr);
}

接下来考虑一下带影响因子的递归形式：

a[k] = f(a[k-x],α) ? g(a[k-y],β) ?......? h(a[k-z],γ) {k>|z|>|x|>|y|且xyz同号，αβγ为影响因子，?为运算法则}

​int recursion(int n, int &arr[], int α, int β,..., int γ){
    if(n<=z)
        return arr[n];
        
    if(!arr[n-x])
        arr[n-x]=recursion(n-x,arr,α,β,...,γ);
    if(!arr[n-y])
        arr[n-y]=recursion(n-y,arr,α,β,...,γ);
    ......
    if(!arr[n-z])
        arr[n-z]=recursion(n-z,arr,α,β,...,γ);

    arr[n] = f(arr[n-x],α) ? g(arr[n-y],β) ?......? h(arr[n-z],γ);
    return arr[n];
}
void test(){
    int n,α,β,...,γ;
    cin>>n;
    cin>>α;
    cin>>β;
    ......
    cin>>γ;

    int arr[n+1]={0};
    arr[1]=a;
    arr[2]=b;
    ......
    arr[z-1]=c;
    arr[z]=d;

    cout<<recursion(n,arr,α,β,...,γ);
}

再由递归到循环：

a[k] = f(a[k-x],α) ? g(a[k-y],β) ?......? h(a[k-z],γ) {k>|z|>|x|>|y|且xyz同号，αβγ为影响因子，?为运算法则}

​void circulation(int n, int &arr[], int α, int β,..., int γ){
    if(n >= arr.numberOfNotZero()){
        for(int i=z+1 ; i<=n ; ++i)
            arr[i] = f(arr[i-x],α) ? g(arr[i-y],β) ?......? h(arr[i-z],γ);
    }
}
void test(){
    int n,α,β,...,γ;
    cin>>n;
    cin>>α;
    cin>>β;
    ......
    cin>>γ;

    int arr[n+1]={0};
    arr[1]=a;
    arr[2]=b;
    ......
    arr[z-1]=c;
    arr[z]=d;

    circulation(n,arr,α,β,...,γ);
}

一些特殊情况的循环是可以优化的：

a[n] = f(a[n-x],α) ? g(a[n-2x],β) ?......? h(a[n-kx],γ) {x>1，n∈N+，αβγ为影响因子，?为运算法则}

​​void circulation(int n, int &arr[], int α, int β,..., int γ){
    if(n >= z){
        int i=n%x+kx;
        while(arr[i])
            i+=x;
        for(; i<=n ; i+=x)
            a[i] = f(a[i-x],α) ? g(a[i-2x],β) ?......? h(a[i-kx],γ);
    }
}
void test(){
    int n,α,β,...,γ;
    cin>>α;
    cin>>β;
    cin>>γ;
    ......
    cin>>k;
    
    int arr[n+1]={0};
    arr[1]=a;
    arr[2]=b;
    ......
    arr[kx-1]=c;
    arr[kx]=d;
    
    circulation(n,arr,α,β,...,γ);
}