处理极限方法

这里归纳了常用的极限处理方法，至少在我考研结束为止这些方法已经足够解决我碰上的绝大多数极限问题。

洛必达

这个方法使用的话就是要注意题目中所给的条件，比如题目中告诉你二阶可导，那就可以用一次洛必达，如果告诉你连续二阶可导，那就可以用两次洛必达。这个就不多证明，直接记住到时候碰到直接用就可以了。

泰勒展开

这个的话，就是背，背下来就可以用，要注意的点是展开公式要展到几阶的问题。有时候我们会说，缺失精度就是因为展开的阶数不够。

关于展开阶数的确定一个是看分母，比如

                                                               

这里要展到几阶？ 展到，因为这里分母阶数是3。

泰勒公式这里直接给出了嗷，省得之后还得去其他博主那里 翻 

等价无穷小代换

（我们上大一的时候老师都说加减法不可以等价代换是因为这个使用是有条件的，而当时我们又没有必要学的那么深，所以直接告诉我们说不可以等价代换，但实际上只要是符合条件的加减法同样可以进行等价代换，尤其是考研的时候这种方法会很常见）

这个我的理解就是青春版洛必达，别人用洛必达简化一下就是你看到的那些等价代换了。等价代换使用的时候注意了嗷，如果是除法，比如f（x）/g（x）那么这个时候你可以分别对fx或gx进行等价代换，但是如果是加减法，是有使用条件的。

这里这个条件要看好，当你不确定是否可以在加减法中进行等价代换

（比如），你就写成lim f（x）/g（x）的形式如果结果是1那么就不可以等价代换，如果是其他数字那么就可以等价代换注意这里我写的是fx-gx，一定记得不要只靠想的，静下心来列出来写一下看看是不是1，费不了多少时间的。

还有就是你注意这里他的原理就是你不可以把这两个等价完之后相减为0，所以1和-1的情况你要看清楚了哦。

这里两张图建议都记下来，这里所有的东西都是我考完研发现一定会用到的，迟早要背的。 当然记得多写点题目，写熟练了就不会忘记啦~

等价代换

这个的话直接看图吧，有不理解的踢我一下我后期补充。

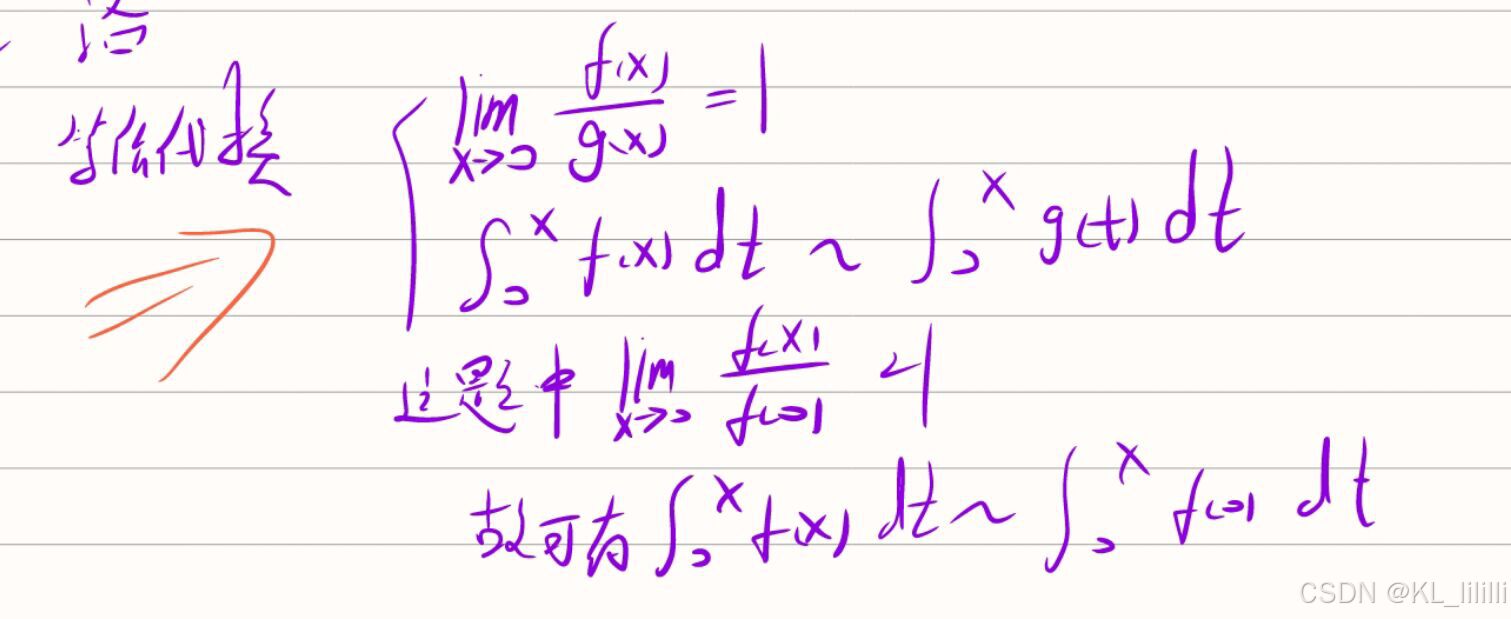
积分中值定理

上图，这个直接用就好了，没什么需要注意的。

这些方法掌握那基本上所有的题目都能写了。不过因为没找到合适的题目所以这篇文章里没有例子，如果看了有点不理解，也可以拿题目私信我，我给你讲完顺便重新补充一下文章。天天开心！

关于高数的大部分文章都会持续完善更新，因为不知道这样子写能不能帮助到你.....所以这里以npy为标准，她要是看完这篇文章觉得没问题能写题目了那这篇文章就不会再继续修改更新....

修改次数（3）