本文转自 http://www.cnblogs.com/ubunoon/
贝叶斯抠图,主要是利用贝叶斯定理来进行点颜色的概率计算。
一、前景色和背景色关系
对于前景色,背景色以及当前显示的颜色,存在下面的一个关系:
其中F表示前景色,B表示背景色,C表示当前颜色,α则表示不透明度。
二、贝叶斯定理
贝叶斯定理是关于随机事件A和B的条件概率和边缘概率的一则定理。
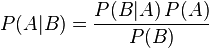
其中P(A|B)是在B发生的情况下A发生的可能性。
在贝叶斯定理中,每个名词都有约定俗成的名称:
· P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
· P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
· P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
P(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)
按这些术语,Bayes定理可表述为:
- 后验概率 = (相似度*先验概率)/标准化常量
三、最大后验概率
假设我们需要根据观察数据 x 估计没有观察到的总体参数 θ,让 f 作为 x 的采样分布,这样 f(x | θ) 就是总体参数为 θ 时 x 的概率。函数
即为似然函数,其估计
就是 θ 的最大似然估计。
假设 θ 存在一个先验分布 g,这就允许我们将 θ 作为 贝叶斯统计中的随机变量,这样 θ 的后验分布就是:
其中 Θ 是 g 的domain,这是贝叶斯定理的直接应用。
最大后验估计方法于是估计 θ 为这个随机变量的后验分布的众数:
后验分布的分母与 θ 无关,所以在优化过程中不起作用。注意当前验 g 是常数函数时最大后验估计与最大似然估计重和。
最大后验估计可以用以下几种方法计算:
- 解析方法,当后验分布的模能够用 closed form 方式表示的时候用这种方法。当使用conjugate prior 的时候就是这种情况。
- 通过如共扼积分法或者牛顿法这样的数值优化方法进行,这通常需要一阶或者导数,导数需要通过解析或者数值方法得到。
- 通过 期望最大化算法 的修改实现,这种方法不需要后验密度的导数。
四、贝叶斯抠图
显然对于一幅给定的图片,当前表示的颜色是知道的,其他的变量是未知的。依据最大后验概率和贝叶斯定理:
使用乘法计算,数值计算量大且计算方式麻烦,因此采用对数方式将乘法改为加法,得到
此处忽略掉了P(C),因为对于参数优化而言,这是一个常量,对于max而言,并没有贡献。于是剩下的问题是解决L(C|F,B,α), L(F), L(B), L(α),在应用前景色与背景色的关系后,可以得到
对数形式的C测量值模型误差是符合高斯概率分布的,其平均值为![]() ,
,![]() 为标准方差。
为标准方差。
使用图像的空间连贯性来评估前景色L(F),也就是通过用已知的先前评估的概率分布来构建每个颜色领域N的颜色概率分布。为使得前景分布的模型更加健壮,依据两个分隔因子,使用每个像素i在N附近的权重贡献。首先,通过![]() (更多考虑不透明色的)计算像素贡献值,,其次,使用
(更多考虑不透明色的)计算像素贡献值,,其次,使用![]() 的空间高斯衰减
的空间高斯衰减![]() 来强调区分附近像素的贡献与futher away像素的贡献,这两个叠加起来就是权重:
来强调区分附近像素的贡献与futher away像素的贡献,这两个叠加起来就是权重:![]()
对于给定的前景色和相关的权重,将颜色通过Orchard和Bouman的方法分开为多个cluster。对于每一个cluster,计算加权平均颜色![]() 和加权协方差矩阵
和加权协方差矩阵![]()
此处![]() ,即权重的累积和。L(F)可以被模型为从面向的椭圆高斯分布,使用权重协方差矩阵:
,即权重的累积和。L(F)可以被模型为从面向的椭圆高斯分布,使用权重协方差矩阵:
因此L(F)的问题被解决了,对于自然图像,设置wi为![]() ,并用B取代F,就可以得到L(B)的计算方法了。
,并用B取代F,就可以得到L(B)的计算方法了。
对于常量颜色的抠图,计算所有被标记位背景的像素集合的平均值和协方差。对于不同的抠图,对于每一个像素使用不同的背景色,因此我们得到了已知背景色的平均值和用户定义变量模型下的背景噪音。
我们假定不透明的L(α)是常量(因此在矩阵中忽略),从实际alpha抠图中统计得到的良好定义L(α),将留给以后的工作。
由于α,F和B之间的乘积的对数L(C|F,B,α),最大化的后验不是已知的二次方程。为有效解决方程,将问题分解为两个子二次方程,
第一个子问题,假定α是常量,在该假定下,对(import)进行偏导数,并使得等式等于0(极值问题),于是可以得到:
此处I是3x3的单位矩阵,因此,对于常数α来说,通过计算6x6的线性方程,可以找到最佳的参数F和B。
第二个子问题,假定F和B是常量,产生一个α的二次方程,引入观察量C作为颜色空间线段FB:
此处数据在两个颜色向量中包含一个点积,为优化等式(import),我们选择假定α来得到F和B,假定F和B来得到α,优化开始前,先初始化α为像素附近值的平均α,然后解决常量α的等式。
当有多个前景色或背景色的cluster,我们运行为每一个前景色和背景色cluster对进行上述优化过程,选择最大的L对。注意这个模型,与高斯混合模型相反,假定观察颜色对应于前景和背景分布的确切对。在某些情况下,该模型可能是矫正模型,但我们当然可以设想需要高斯混合模型的案例,当前景cluster可以和另外空间临近,然后可以在颜色空间中混合。理想情况下,我们支持一个贝叶斯混合模型,实际上,及时我们简单排除设定模型,我们可以得到比存在方法得到更好的解决结果。
后记:
虽然理论上已经解决了一大部分,还有个理论问题点没有解决,即Orchard和Bouman方法的颜色聚类方式,将在下一篇中进行该方式解答。
参考:
贝叶斯定理:http://zh.wikipedia.org/wiki/%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%AE%9A%E7%90%86
最大后验概率:http://zh.wikipedia.org/wiki/%E6%9C%80%E5%A4%A7%E5%90%8E%E9%AA%8C%E6%A6%82%E7%8E%87
贝叶斯抠图:http://grail.cs.washington.edu/projects/digital-matting/
*
* Copyright (c) 2011 Ubunoon.
* All rights reserved.
*
* email: netubu#gmail.com replace '#' to '@'
* http://www.cnblogs.com/ubunoon
* 欢迎来邮件定制各类验证码识别,条码识别,图像处理等软件








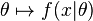
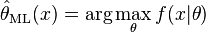
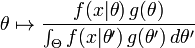
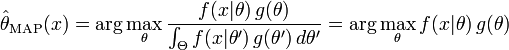


















 283
283

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








