基于C++实现网格细化粗化

1. 实验步骤与内容：

• 成功调通代码，实现模型的加载与边的显示。

这一部分内容比较麻烦的问题是 make 中依赖包的获取，运行所给代码的第一步就是 make，之后就是解决缺少库的问题。（如下图 find_package 找不到）

因为用的是 win10 平台，解决方案是装了一个 vcpkg，把路径输入到 cmake 设置里面，就能把从 vcpkg 下载的包导入 cmake 项目了，编译生成工作得以顺利进行。然后就可以通过命令行运行 exe 得到程序的运行效果了。

• Loop Subdivision

这一部分是构造 LoopSubdivision 函数，在这一个函数中，我们先要实现一般的细分,也就是说在每个边找它的中点，这样，一个三角形就被分成了四个三角形。

具体的代码实现在 mesh.cpp 里面的 SimpleSubdivision()函数。

代码的大体思路是，首先统计所有三角形的代表边。之后对每一个代表边，我们求出它的中点，并通过 getNext 函数求出所代表三角形的其他边的中点，之后删除这个边代表的三角形，通过三个中点三个原有点构造四个三角形即可，比较简单。

其中需要注意的问题是点复用，我的解决方案是在每次构建三角形前，先看看他的顶点坐标是不是已经被创建点了，已经被创建了就拿过来用，没有就建个新的。

简单细化截图：

我把生成的 exe 文件打包了，Sub 文件夹里面就是简单细化的可执行程序，可以通过双击直接打开测试，按 s 细化。

下一步是引入 LoopSub 规则，我是发现了，其实 Loop 和 Butterfly，都是根据临近点综合生成新点进行插值。只不过 Loop 动的是原有点，Butterfly 动的是新加入的中点。这里我们先讨论 LoopSub，他的规则重点大致就两个，一是决定新点位置，这个比较简单，如果是内点走这个公式。

如果是边点那就是 1/2（v0+v1）

然后就是决定原有点的位置，这个就比较复杂了。为了说的清楚，引用了部分资料内容。（注：仅为解释算法需要非抄袭）

首先是内点

假设原有的内部顶点为 v0，相邻顶点为 v1，v2，v3，v4…vn，那么移动后的 v0 的坐标 v 为：

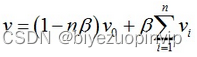
本质是顶点本身与相邻顶点的加权和，它本身的权值为(1-nβ)，其邻接点的权值为 β。这里权值 β 通过下式计算得到：

边界点 v=3/4v0+1/8v1+1/8+v2

根据以上 loopsub 的思想，我开始写代码，思想看起来很简单，实现起来有好多问题，尤其是边界点的判断和处理，做的挺吃力，但好在解决了。

我的代码思路一开始根简单细分一样，也是先统计现有三角形代表边，以此为基础进行遍历。对每一个代表边，都要先确定新的中点位置，这个需要先判断是不是边界点，依靠 getopposite 是不是 NULL 来判断，根据结果找不同的点，带入不同的公式。

确定好新的中点，再来确定原来点的位置，这里我犯了个错误卡了半天出不来，那就是我先把新的点连成三角形再去找原来点的新位置，弄了半天不对。后来才明白过来，不能先连三角，而是先把一个三角的所有点位置找到一块连。

计算原来点的新位置，就要遍历原来点的邻接点，并在遍历的过程确定是不是边界点，这个过程比较复杂，我的思路是

其实就是顺走，逆反，记录点，顺走，逆反，记录点直到转一圈为止。

假如中间逆反为空也就是到边了，我的思路是点记录清零，反向寻路重新记录知道另外一个边界，反向寻路之前要先记录边点的 getendvertrx，之后顺走两次记录点，逆反，顺走两次记录点。

之后就是根据收集到的临界点和对是否是边界点的判断，带入相应的公式，求的原点的新坐标，最后连接所有 6 个新得到的点即可得到四个新三角行，删除原有三角即可。

LoopSub 截图：

可执行文件在 SubLoop 文件夹中，双击测试，按 s 细化。

• Implement the butterfly interpolating subdivision surface scheme

Butterfly 算法在我看来要比 Loop 算法简单一点，毕竟只是动新加的中点，原点都不用动，然而事实证明，有拓展的蝴蝶算法实现起来还是有一些坑的。

首先是算法思想。以下称新加入的中点为奇点。为了解释清楚引用部分资料内容。（注：仅为解释算法需要非抄袭）

当该奇点所在边的两个端点的度均为 6 时

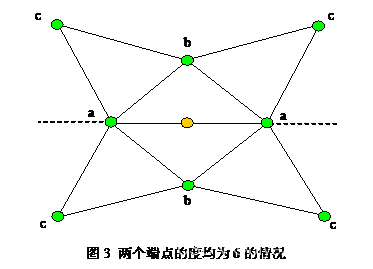
它的坐标值通过周围八个点（绿色）的坐标值加权平均得到。并且周围的点按权重不同可分为三类，各自权重如下

a= 1/2，b = 1/8，c = -1/16

当该奇点所在边的两个端点中，一个端点的度为 6，另一个不为 6 时

则奇点的坐标值要根据点 v 及 v 的所有相临结点（绿色）的坐标加权得到。v 点的权重如下：

v = 3/4

假设点 v 共有 n 个邻结点，则各邻结点的权值可根据 n 值的不同分别计算：

• n= 3 时：e0 = 5/12，e1 = e2 = -1/12；
• n= 4 时：e0 = 3/8，e1 = 0，e2 = -1/8，e3 = 0；
• n≥ 5 时：ej = [1/4 + cos(2∏j/n) + 1/2 * cos(4∏j/n)]/n，其中 j = 0，1，…，n-1。
• 当该新边点所在边的两个端点的度均不为 6 时

先以 v1 为中心，按前述（b）情况中的方法计算出奇点的坐标，记为(x1，y1，z1)，再以 v2 为中心同样计算出奇点的坐标，记为(x2，y2，z2)，然后对两组坐标取平均值，得到奇点的坐标。

当该奇点所在边是初始控制网的边界时

此时参与计算的各点的权值取值如下：

a= 9/16，b = -1/16

我的代码的实现根算法的思路相仿，通过对每一个三角形的边先判断是不是边界边，之后若不是边界边，统计两端点的度数，这里统计端点的临界点的方法和 LoopSub 相一致，区别在于，因为蝴蝶算法对点的位置顺序很有要求，所以我在统计的时候碰到了边界，就不像 LoopSub 那样直接删掉倒着从头统计了，这样位置会乱。我想的办法是碰到了边界就回头找另一个边界，找到另一个边界正着继续统计，直到碰到开始边，这样，总体上就是个从开始边开始的顺（逆）时针统计了，位置很好确定，为之后公式打下基础。

之后就是根据两个端点的度的数量进入不同的公式，计算得出新的中点位置，加上原有的点绘制四个三角形，删除原来的三角形即可。

截图：

可执行文件在 subButterfly 文件夹内，双击运行即可，按 s 细化。

• Test Loop & butterfly scheme with some .obj models

Loop：

Bunny_1k.obj

Monkey2.obj

Butterfly：

Cube.obj

Monkey.obj

• 其实我在老师删掉模型简化实验之前就写了，这里大体说一下吧

模型简化的思想很简单，就是随机挑一个边去掉就 ok，难的是去掉之后剩下的边的合并问题，我选择的是合并到这个边的开始点上，有的人选择合并到这个边的中点上，都可以。我在写的时候遇到的最大的问题就是崩溃，删了原来的一圈三角形重新把这一圈点连到其中一个上会有很多问题，动不动就不符合流型了，我很崩溃啊。最终左思右想解决了，结局的方案是判断新建三角形们是不是都符合流型规范，都符合就建立，万一有个不符合，直接取消一切操作复原之前的一圈三角形，重新找一个边重复过程。

截图：