B站吴恩达深度学习视频笔记（10）——从计算图（Computational Graph）角度计算梯度下降

前言

计算图是一个很重要的概念。在上一篇笔记里面，我们把公式写进小格子里面看作图的一个结点，通过图结点的前驱和后继完成对于参数的更新，以及数值的运算，这就是计算图的用法。为了更好地在神经网络中利用计算图做点事情，这篇笔记会告诉你如何使用计算图计算梯度下降（梯度下降光讲是啥了，还没说怎么算呢）

计算图计算梯度下降

本节我们讨论怎样通过计算偏导数来实现逻辑回归的梯度下降算法。

它的关键点是几个重要公式，其作用是用来实现逻辑回归中梯度下降算法。

但是在本节中，将使用计算图对梯度下降算法进行计算。必须要承认的是，使用计算图来计算逻辑回归的梯度下降算法有点大材小用了。但是，以这个例子作为开始来讲解，可以使你更好的理解背后的思想。从而在讨论神经网络时，你可以更深刻而全面地理解神经网络。

接下来让我们开始学习逻辑回归的梯度下降算法。

假设样本只有两个特征x_1和x_2，为了计算z，我们需要输入参数w_1、w_2 和b，除此之外还有特征值x_1和x_2。因此z的计算公式为： z=w_1 x_1+w_2 x_2+b

回想一下逻辑回归的公式定义如下：

^y=a=σ(z) 其中z=w^T x+b ， σ(z)=1/(1+e^(-z) )

损失函数：

代价函数：

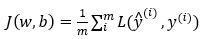
假设现在只考虑单个样本的情况，单个样本的代价函数定义如下：

其中a是逻辑回归的输出，y是样本的标签值。

现在让我们画出表示这个计算的计算图。 这里先复习下梯度下降法，w和b的修正量可以表达如下：

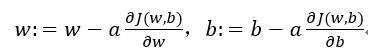
如图：在这个公式的外侧画上长方形。

然后计算： ^y=a=σ(z) 也就是计算图的下一步。最后计算损失函数L(a,y)。

有了计算图，我就不需要再写出公式了。

因此，为了使得逻辑回归中最小化代价函数L(a,y)，我们需要做的仅仅是修改参数w和b的值。前面我们已经讲解了如何在单个训练样本上计算代价函数的前向步骤。

现在让我们来讨论通过反向计算出导数。 因为我们想要计算出的代价函数L(a,y)的导数，首先我们需要反向计算出代价函数L(a,y)关于a的导数，在编写代码时，你只需要用da 来表示(dL(a,y))/da 。

通过微积分得到：

如果你不熟悉微积分，也不必太担心，我会列出本课程涉及的所有求导公式。那么如果你非常熟悉微积分，我们鼓励你主动推导前面介绍的代价函数的求导公式，使用微积分直接求出L(a,y)关于变量a的导数。如果你不太了解微积分，也不用太担心。现在我们已经计算出da，也就是最终输出结果的导数。 现在可以再反向一步，在编写Python代码时，你只需要用dz来表示代价函数L关于z 的导数dL/dz，也可以写成(dL(a,y))/dz，这两种写法都是正确的。 dL/dz=a-y 。

因为

并且da/dz=a⋅(1-a)， 而

因此将这两项相乘

为了简化推导过程，假设n_x这个推导的过程就是我之前提到过的链式法则。

如果你对微积分熟悉，放心地去推导整个求导过程，如果不熟悉微积分，你只需要知道dz=(a-y)已经计算好了。

现在进行最后一步反向推导，也就是计算w和b变化对代价函数L的影响，特别地，可以用:

视频中， dw_1 表示∂L/(∂w_1 )=x_1⋅dz， dw_2 表示∂L/(∂w_2 )=x_2⋅dz， db=dz。

因此，关于单个样本的梯度下降算法，你所需要做的就是如下的事情：

使用公式dz=(a-y)计算dz，

使用

dw_1=x_1⋅dz 计算dw_1，

dw_2=x_2⋅dz计算dw_2，

db=dz 来计算db，

然后:

更新w_1=w_1-adw_1，

更新w_2=w_2-adw_2，

更新b=b-αdb。

这就是关于单个样本实例的梯度下降算法中参数更新一次的步骤。

现在你已经知道了怎样计算导数，并且实现针对单个训练样本的逻辑回归的梯度下降算法。但是，训练逻辑回归模型不仅仅只有一个训练样本，而是有m个训练样本的整个训练集。

因此在下一个笔记中，我们将这些思想应用到整个训练样本集中，而不仅仅只是单个样本上。

梯度下降实现的简单代码，也是在知乎的一位大佬的代码实现出来

# -*- coding: utf-8 -*-
# 先随便猜w1,w2,b是多少
w1 = 0.666
w2 = 0.333
b = 0.233

def train():
    # 用于训练的数据（四行）一行样本数据格式为 [x1,x2,g(x1,x2)]
    data = [
            [1,  0,     -1],
            [0,  1,     -1],
            [0,  0,     -1],
            [1,  1,     1]
            ]
    global w1,w2,b # 告诉计算机我修改的是全局变量（每个函数都能修改这个变量）

    epoch = 20 # 同样的数据反复训练20次
    for _ in range(epoch):
        # 逐个样本更新权重
        for i in data:
            # 这里的i = [x1,x2,g(x1,x2)]，它是data中的一行
            # 求各自导函数在(x1,x2,g(x1,x2))处的导函数值
            d_w1 = 2*(w1*i[0]+w2*i[1]+b-i[2])*i[0]
            d_w2 = 2*(w1*i[0]+w2*i[1]+b-i[2])*i[1]
            d_b = 2*(w1*i[0]+w2*i[1]+b-i[2])

            # 接下来就是愉快的理性猜环节了
            # 设置学习率，防止蹦的步子太大
            learning_rate = 0.01
            # 下次猜的数 = 本次猜的数 - 学习率*导数值
            w1_next = w1 - learning_rate*d_w1
            w2_next = w2 - learning_rate*d_w2
            b_next = b - learning_rate*d_b

            # 更新各参数
            w1 = w1_next
            w2 = w2_next
            b = b_next

            pass
        pass

def f(x1,x2):
    """
    这是一个神经元（本质就是一个表达式）
    经过训练，我们期望它的返回值是x1&x2
    返回值是 w1*x1+w2*x2 + b > 0? 1:0;
    计算这个用于判断(x0,x1)的分类。
    大于0则是点(x0,x1)在右上输出1，小于0则点在左下输出0；
    """
    global w1,w2,b # 告诉计算机我修改的是全局变量（每个函数都能修改这个变量）
    if w1*x1+w2*x2 + b > 0:
        return 1
    else:
        return 0

# 我们首先执行下训练，让神经元自己根据四条数据学习逻辑与的规则
train()
# 打印出模型计算出来的三个比较优的参数
print(w1,w2,b)
"""
输出：0.4514297388906616 0.2369025056182418 -0.611635769357402
"""

# 好我们测试下，看神经元有没有自己学习到逻辑与的规则
print("0&1",f(0,1))
print("1&0",f(1,0))
print("0&0",f(0,0))
print("1&1",f(1,1))
"""
输出：
0&1= 0
1&0= 0
0&0= 0
1&1= 1
"""