LoRA原理详解+问题解答+代码实现LoRA

一、前言

通常使用大模型全量精调会出现一下问题：

• ⼤模型通常包含数亿甚⾄数百亿个参数，对其进⾏微调需要⼤量的计算资源和存储空间。
• 在微调过程中，直接修改预训练模型的所有参数可能会破坏模型的原始性能。
• 存储和部署微调后的⼤模型需要⼤量存储空间，尤其是当需要在多个应⽤场景中部署不同微调版本时。
• 许多微调⽅法会增加推理阶段的计算延迟，影响模型的实时性应⽤。

LoRA可以有效的解决以上问题
LoRA优势：

• 存储与计算效率：通过低秩适应（LoRA），可以显著减少所需存储的参数数量，并减少计算需求
• 适应性与灵活性：LoRA⽅法允许模型通过只替换少量特定的矩阵A和B来快速适应新任务，显著提⾼任务切换的效率。
• 训练与部署效率：LoRA的简单线性设计允许在不引⼊推理延迟的情况下，与冻结的权重结合使⽤，从⽽提⾼部署
  时的操作效率。

二、Lora原理

预训练模型虽然是过参数化的，但在微调时参数更新主要集中在⼀个低维⼦空间，⾼维参数空间中的⼤部分参数在微调前后⼏乎没有变化。所以通过LoRA可以在低维度中进⾏优化，大大减少微调时需要更新的参数量。低秩分解使参数优化更⾼效，但如果参数更新实际上在⾼维⼦空间中发⽣，可能会导致重要信息遗漏和LoRA⽅法失效。

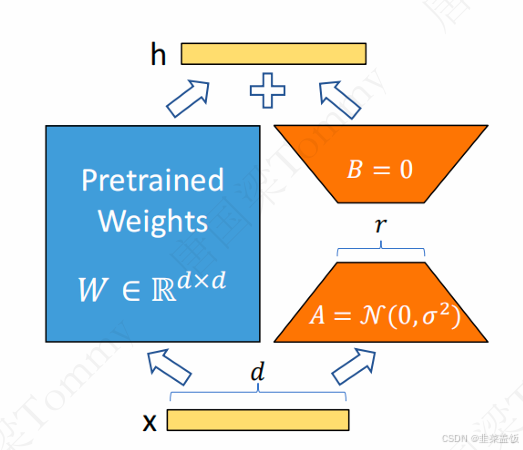
LoRA 通过冻结预训练的权重矩阵 ，仅学习⼀个较⼩的偏置矩阵 ，公式如下：

A 是⼀个随机初始化的矩阵，且服从正态分布 A~N(0，1)
B 初始化为零矩阵，即B=0，随着训练的进⾏， B 的值逐渐变得⾮零 。

秩r << d ，只有 d*r+r*d参数需要训练(原来需要d*d的参数需要训练)，减少了计算梯度所需的内存和浮点运算量（FLOPS）

三、面试问题

1、为什么B矩阵初始化为0？

这种初始化⽅法使得在训练初期，新增的部分 $△W=BA$对原始权重 W p r e t r a i n e d W_{pretrained} W