DP基础题型及解题思路总结
一、解题一般思路
①、状态表示:
( 1 ) 、 集 合 : 合 法 的 所 有 方 案 的 集 合 (1)、集合:合法的所有方案的集合 (1)、集合:合法的所有方案的集合
( 2 ) 、 属 性 : M a x / M i n / C o u n t (2)、属性:Max/Min/Count (2)、属性:Max/Min/Count
②、状态计算—集合的划分:
划 分 依 据 — — 最 后 一 个 不 同 的 点 划分依据——最后一个不同的点 划分依据——最后一个不同的点
二、01背包问题
题目:
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
分析:
①
、
状
态
表
示
:
数
据
范
围
[
0
,
1000
]
,
意
味
着
状
态
中
可
能
含
1
或
者
2
个
变
量
,
用
d
p
[
i
]
[
j
]
来
表
示
考
虑
前
i
个
物
品
,
物
品
总
体
积
不
超
过
j
的
方
案
中
的
最
大
值
。
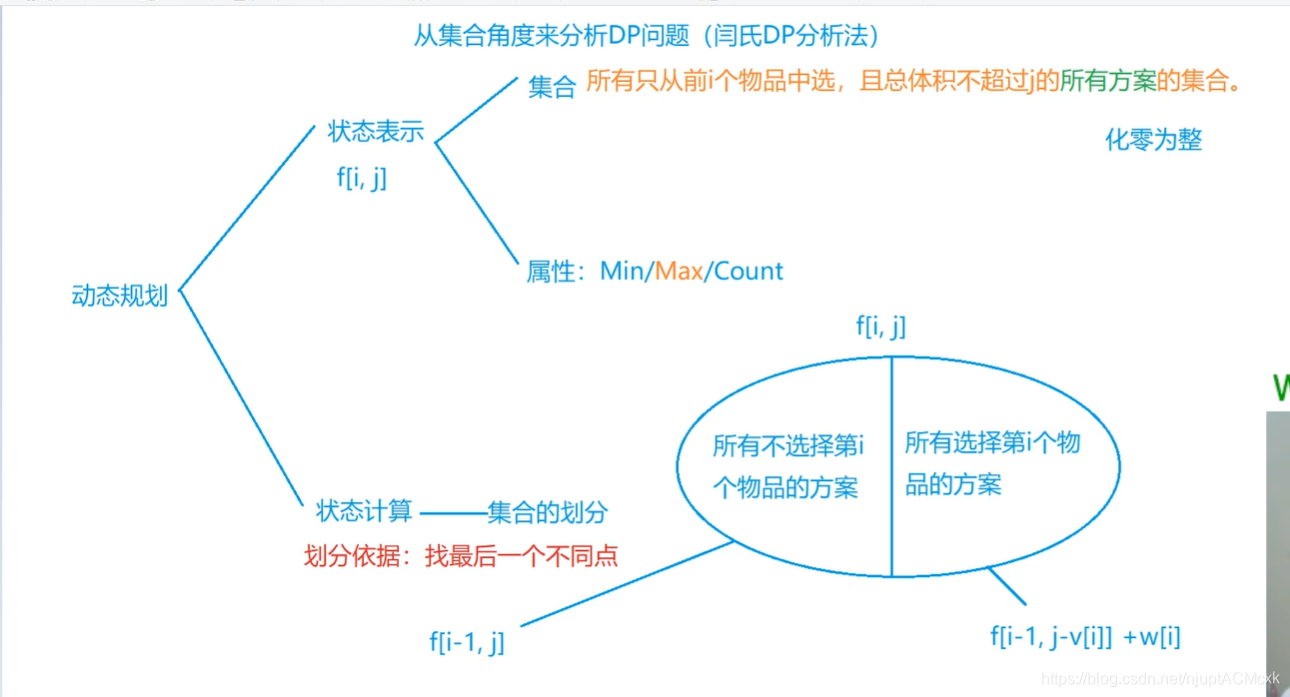
①、状态表示:数据范围[0,1000],意味着状态中可能含1或者2个变量,用dp[i][j]来表示考虑前i个物品,物品总体积不超过j的方案中的最大值。
①、状态表示:数据范围[0,1000],意味着状态中可能含1或者2个变量,用dp[i][j]来表示考虑前i个物品,物品总体积不超过j的方案中的最大值。
② 、 状 态 计 算 : 对 每 一 个 物 品 而 言 , 只 有 取 和 不 取 两 种 状 态 。 考 虑 第 i 件 物 品 : ②、状态计算:对每一个物品而言,只有取和不取两种状态。考虑第i件物品: ②、状态计算:对每一个物品而言,只有取和不取两种状态。考虑第i件物品:
Ⅰ 、 不 取 第 i 件 物 品 , 意 味 着 在 前 i − 1 件 物 品 已 经 取 到 j 体 积 的 物 品 , 最 大 值 是 d p [ i − 1 ] [ j ] 。 Ⅰ、不取第i件物品,意味着在前i-1件物品已经取到j体积的物品,最大值是dp[i-1][j]。 Ⅰ、不取第i件物品,意味着在前i−1件物品已经取到j体积的物品,最大值是dp[i−1][j]。
Ⅱ 、 取 第 i 件 物 品 , 意 味 着 在 前 i − 1 件 物 品 已 经 取 到 j − v [ i ] 体 积 的 物 品 , 最 大 值 是 从 前 i − 1 件 物 品 中 取 j − v [ i ] 体 积 物 品 的 最 大 价 值 + 第 i 件 物 品 的 价 值 。 Ⅱ、取第i件物品,意味着在前i-1件物品已经取到j-v[i]体积的物品,最大值是从前i-1件物品中取j-v[i]体积物品的最大价值+第i件物品的价值。 Ⅱ、取第i件物品,意味着在前i−1件物品已经取到j−v[i]体积的物品,最大值是从前i−1件物品中取j−v[i]体积物品的最大价值+第i件物品的价值。
于 是 得 到 状 态 转 移 方 程 : d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − v [ i ] ] + w [ i ] ) 。 于是得到状态转移方程:dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])。 于是得到状态转移方程:dp[i][j]=max(dp[i−1][j],dp[i−1][j−v[i]]+w[i])。
注 意 : d p [ i − 1 ] [ j − v [ i ] ] + w [ i ] 只 有 在 j > = v [ i ] 的 情 况 下 才 会 考 虑 , 代 码 如 下 : 注意:dp[i-1][j-v[i]]+w[i]只有在j>=v[i]的情况下才会考虑,代码如下: 注意:dp[i−1][j−v[i]]+w[i]只有在j>=v[i]的情况下才会考虑,代码如下:
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=1e3+5;
int N,V,v[maxn],w[maxn];
int dp[maxn][maxn];//dp[i][j] 前i件物品中体积不超过j的最大价值
int main()
{
cin>>N>>V;
for(int i=1;i<=N;i++)
scanf("%d%d",&v[i],&w[i]);
for(int i=1;i<=N;i++)
for(int j=1;j<=V;j++)
{
dp[i][j]=dp[i-1][j];//取不了要保持
if(j>=v[i])
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);
}
cout<<dp[N][V]<<endl;
return 0;
}
改进:
从 上 述 转 移 方 程 中 我 们 发 现 , 前 i 件 的 最 大 价 值 仅 与 前 i − 1 件 的 最 大 价 值 有 关 , 因 此 考 虑 优 化 d p 数 组 空 间 , 第 一 维 空 间 可 以 直 接 删 去 。 得 到 : 从上述转移方程中我们发现,前i件的最大价值仅与前i-1件的最大价值有关,因此考虑优化dp数组空间,第一维空间可以直接删去。得到: 从上述转移方程中我们发现,前i件的最大价值仅与前i−1件的最大价值有关,因此考虑优化dp数组空间,第一维空间可以直接删去。得到:
for(int i=1;i<=N;i++)
for(int j=v[i];j<=V;j++)
{
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
注 意 : 在 原 转 移 方 程 : d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − v [ i ] ] + w [ i ] ) 中 , d p [ i − 1 ] [ j − v [ i ] ] 是 在 d p [ i ] [ j ] 之 前 被 计 算 出 的 , 因 此 , 对 上 述 优 化 过 的 循 环 中 , 要 将 第 二 层 循 环 j 从 大 到 小 枚 举 。 注意:在原转移方程:dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])中,dp[i-1][j-v[i]]是在dp[i][j]之前被计算出的,因此,对上述优化过的循环中,要将第二层循环j从大到小枚举。 注意:在原转移方程:dp[i][j]=max(dp[i−1][j],dp[i−1][j−v[i]]+w[i])中,dp[i−1][j−v[i]]是在dp[i][j]之前被计算出的,因此,对上述优化过的循环中,要将第二层循环j从大到小枚举。
01 背 包 问 题 一 维 写 法 : 01背包问题一维写法: 01背包问题一维写法:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=1e3+5;
int N,V,v,w;
int dp[maxn];//dp[i]所拿物品体积不超过i的最大价值
int main()
{
cin>>N>>V;
for(int i=1;i<=N;i++)
{
scanf("%d%d",&v,&w);
for(int j=V;j>=v;j--)//从大到小
dp[j]=max(dp[j],dp[j-v]+w);
}
cout<<dp[V]<<endl;
return 0;
}
三、摘花生
题目:
Hello Kitty想摘点花生送给她喜欢的米老鼠。
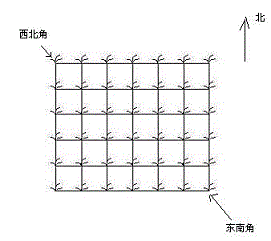
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数T,代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据,从北向南依次描述每行花生苗的情况。每行数据有C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
1≤T≤100,
1≤R,C≤100,
0≤M≤1000
输入样例:
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例:
8
16
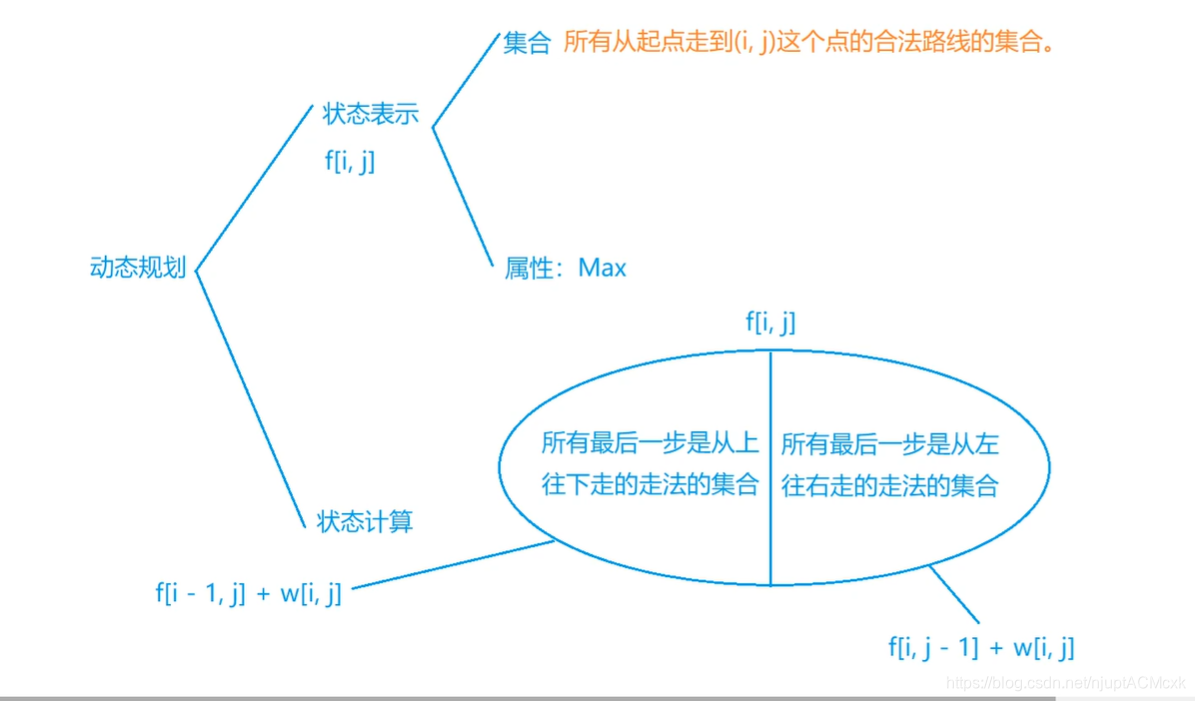
分析:
代码:
//AcWing-1015. 摘花生
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N=105;
int T,R,C;
int mp[N][N];
int dp[N][N];
int main()
{
cin>>T;
while(T--)
{
memset(mp,0,sizeof(mp));
cin>>R>>C;
for(int i=1;i<=R;i++)
for(int j=1;j<=C;j++)
scanf("%d",&mp[i][j]);
/*
dp[1][1]=mp[1][1];
for(int i=1;i<=R;i++)
for(int j=1;j<=C;j++)
if(i==1&&j==1) continue;
else dp[i][j]=max(dp[i-1][j]+mp[i][j],dp[i][j-1]+mp[i][j]);*/
//上述dp过程的优化
for(int i=1;i<=R;i++)
for(int j=1;j<=C;j++)
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+mp[i][j];
cout<<dp[R][C]<<endl;
}
return 0;
}
四、最长上升子序列
题目:
给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数N。
第二行包含N个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N≤1000,
−109≤数列中的数≤109
输入样例:
7
3 1 2 1 8 5 6
输出样例:
4
分析:
①
、
状
态
表
示
:
d
p
[
i
]
:
以
第
i
个
数
结
尾
的
严
格
单
调
上
升
子
序
列
的
集
合
(
若
考
虑
前
i
个
数
字
上
升
最
大
值
会
比
较
麻
烦
)
。
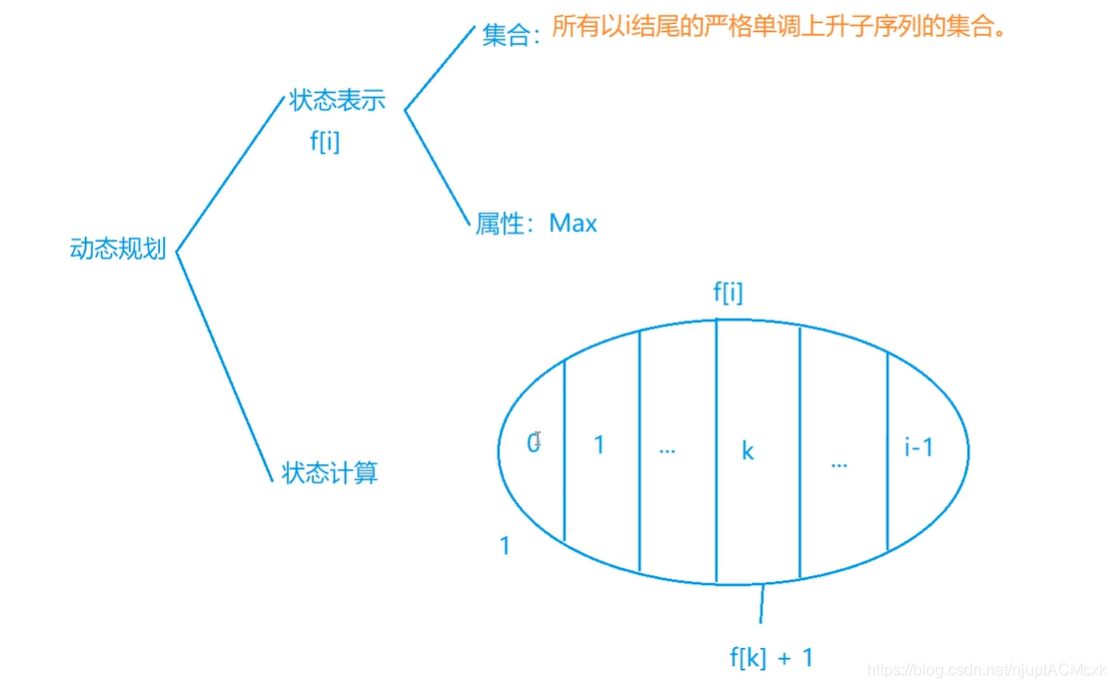
①、状态表示:dp[i]:以第i个数结尾的严格单调上升子序列的集合(若考虑前i个数字上升最大值会比较麻烦)。
①、状态表示:dp[i]:以第i个数结尾的严格单调上升子序列的集合(若考虑前i个数字上升最大值会比较麻烦)。
② 、 状 态 计 算 : 考 虑 最 后 一 个 “ 不 同 点 ” : 由 于 对 于 d p [ i ] 集 合 中 , 最 后 一 个 数 字 都 相 同 , 故 考 虑 倒 数 第 二 个 数 字 。 倒 数 第 二 个 数 字 有 i 种 情 况 , 可 能 不 存 在 ( d p [ i ] = 1 , 只 有 一 个 数 字 ) , 也 可 能 是 第 1 , 2 , . . . , i − 1 个 数 字 。 ②、状态计算:考虑最后一个“不同点”:由于对于dp[i]集合中,最后一个数字都相同,故考虑倒数第二个数字。\\倒数第二个数字有i种情况,可能不存在(dp[i]=1,只有一个数字),也可能是第1,2,...,i-1个数字。 ②、状态计算:考虑最后一个“不同点”:由于对于dp[i]集合中,最后一个数字都相同,故考虑倒数第二个数字。倒数第二个数字有i种情况,可能不存在(dp[i]=1,只有一个数字),也可能是第1,2,...,i−1个数字。
故 d p [ i ] = m a x ( d p [ i ] , d p [ j ] + 1 ) , j ∈ [ 0 , i − 1 ] 。 故dp[i]=max(dp[i],dp[j]+1),j∈[0,i-1]。 故dp[i]=max(dp[i],dp[j]+1),j∈[0,i−1]。
注 意 边 界 问 题 : 每 一 遍 更 新 d p [ i ] 时 要 初 始 话 为 1 , 也 就 是 倒 数 第 二 个 数 字 不 存 在 的 情 况 。 注意边界问题:每一遍更新dp[i]时要初始话为1,也就是倒数第二个数字不存在的情况。 注意边界问题:每一遍更新dp[i]时要初始话为1,也就是倒数第二个数字不存在的情况。
最 后 取 所 有 d p 结 果 中 的 最 大 值 即 可 。 最后取所有dp结果中的最大值即可。 最后取所有dp结果中的最大值即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
int N;
ll a[1005];
int dp[1005];//dp[i]以a[i]结尾的子序列的最大值
int main()
{
cin>>N;
for(int i=1;i<=N;i++)
cin>>a[i];
for(int i=1;i<=N;i++)
{
dp[i]=1;//倒数第二个数不存在的情况
for(int j=1;j<i;j++)
{
if(a[i]>a[j])
dp[i]=max(dp[i],dp[j]+1);//a[i]是max(dp[1~i-1])+1
}
}
int ans=0;
for(int i=1;i<=N;i++)
ans=max(ans,dp[i]);
cout<<ans<<endl;
return 0;
}





















 1108
1108











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








