2022-07-18 至 2022-07-25 记录

nth2000

已于 2022-07-24 12:09:16 修改

阅读量328

点赞数

文章标签：算法 c++ 图论

于 2022-07-18 13:29:59 首次发布

本文链接：https://blog.csdn.net/nth2000/article/details/125846733

版权

Zero Path（1700）

题目大意：给定n*m方阵，每个格点上有1或-1。每次只能向右移动一步或者向下移动一步。问是否存在从起始点(1,1)到(n,m)一条和为0的路径。
思路：
关键在于充分利用方阵上的-1,1，增量时仅会造成很小变化，可能在变化的途中达到目标值。（先找到某个范围）

从起点到终点走的格点数是固定的，都是n+m-1。因此n+m-1为奇数时，不可能达成目标。而n+m-1为偶数时，由于奇+奇=偶，奇-奇=偶，因此到达(n,m)点的所有路径和都为偶数。
使用dp容易求得路径和的最大值和最小值(必要条件)。如果[最小值，最大值]包含0，则最终答案包含0。这是因为可以移动每次上下水平向右移动的步骤使得路径和变为最大值。使用方阵上的-1，1的条件，每次移动改变路径和-2或2。于是一定某次移动后路径和变为0
反思：这种思想以前是遇到过的，见那个很妙的滑动窗口均值的题(juju and binary string 2800)。
另一种思路：运用bitset dp记录和。

#include <bits/stdc++.h>
using namespace std;
vector<bool> vis;


int main()
{
    int t; cin>>t;
    for(int i  =0 ;i<t;i++)
    {
        int n,m;
        scanf("%d %d",&n,&m);
        int d[n][m];
        for(int  k = 0;k<n;k++) for(int q = 0;q<m;q++) scanf("%d",&d[k][q]);
        if((n+m-1)%2==1) {printf("NO\n");continue;}
        int dpmin[n][m],dpmax[n][m];
        dpmin[0][0]=dpmax[0][0]=d[0][0];
        for(int i = 0;i<n;i++)
        {
            for(int j = 0;j<m;j++)
            {
                if(i==0&&j==0) continue;
                int a = INT_MIN;  //用于更新最大值
                int b = INT_MAX;  //用于更新最小值
                if(i-1>=0) {a = max(a,dpmax[i-1][j]); b = min(b,dpmin[i-1][j]);}
                if(j-1>=0) {a = max(a,dpmax[i][j-1]);    b = min(b,dpmin[i][j-1]);}
                dpmax[i][j] = a + d[i][j];
                dpmin[i][j] = b + d[i][j];
            }
        }
        if(dpmin[n-1][m-1]<=0 && dpmax[n-1][m-1]>=0) printf("YES\n"); else printf("NO\n");
    }
    system("pause");
}

Max GEQ Sum（1800）

题目大意：
给定数组a，判断是否存在一个连续子数组，使得其最大值大于等于其和。
思路：
和leetcode某次周赛类似(threhold那道题)，以每个点作为最大值划分解空间。设当前点下标为i,左边连续最后一个小于等于a[i]的数下标为x，右边连续最后一个小于等于a[i]的数的下标为y（采用单调栈 $O (n)$ 做出）。
然后判断 $\leq u \leq i - 1$ 和 $\leq o \leq y$ 这一系列子数组和是否至少有一个大于 $a_i$ 即可，这可以使用前缀和，后缀和+线段树在 $\log n)$ 内实现。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll pretree[9500001];
ll suftree[9500001];


void build(int s, int t, int p,ll d[]) {
  // 对 [s,t] 区间建立线段树,当前根的编号为 p
  if (s == t) {
    d[p] = -1e18;
    return;
  }
  int m = s + ((t - s) >> 1);
  // 移位运算符的优先级小于加减法，所以加上括号
  // 如果写成 (s + t) >> 1 可能会超出 int 范围
  build(s, m, p * 2,d), build(m + 1, t, p * 2 + 1,d);
  // 递归对左右区间建树
  d[p] = -1e18;
}


ll query(int l, int r, int s, int t, int p,ll d[]) {
  // [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号
 // if(r < l) return LONG_LONG_MIN + 1e18;
  if (l <= s && t <= r)
    return d[p];  // 当前区间为询问区间的子集时直接返回当前区间的和
  int m = s + ((t - s) >> 1);
  ll ans = LONG_LONG_MIN;
  if (l <= m) ans = max(ans,query(l, r, s, m, p * 2,d));
  // 如果左儿子代表的区间 [l, m] 与询问区间有交集, 则递归查询左儿子
  if (r > m) ans = max(ans,query(l, r, m + 1, t, p * 2 + 1,d));
  // 如果右儿子代表的区间 [m + 1, r] 与询问区间有交集, 则递归查询右儿子
  return ans;
}

// C++ Version
void update(int index,ll c, int s, int t, int p, ll d[]) {
  if (s == t && s== index) {
    d[p] = max(d[p],(ll)c);
    return;
  } 
  int m = s + ((t - s) >> 1);
  if(index <= m) update(index,c,s,m,2*p,d);
  else update(index,c,m+1,t,2*p+1,d);
  d[p] = max(d[p*2],d[p*2+1]);
}



int main()
{
    int t;
    scanf("%d",&t);
    for(int i = 0;i<t;i++)
    {
        int n; scanf("%d",&n);
        int a[n];
        for(int  k = 0;k<n;k++) scanf("%d",&a[k]);
        ll pre[n]; pre[0]=a[0]; for(int k = 1;k<n;k++) pre[k]=pre[k-1]+a[k];
        ll suf[n]; suf[n-1]=a[n-1]; for(int k = n - 2;k>=0;k--) suf[k] = suf[k+1]+a[k];
        //找左侧第一个大于自身元素的index 
        int l[n];
        //找右侧第一个大于自身元素的index
        int r[n];
        stack<int> s;    //当前元素的Index
        l[0] = -1;  
        s.push(0);
        for(int k = 1;k<n;k++)
        {
            while(!s.empty() && a[s.top()] <= a[k]) 
                s.pop();
            if(!s.empty()) {l[k]=s.top();} else l[k]=-1;
            s.push(k);
        }
        while(!s.empty()) s.pop();
        r[n-1] = n; s.push(n-1);
        for(int k =  n-2;k>=0;k--)
        {

            while(!s.empty() && a[s.top()] <= a[k]) 
                s.pop();
            if(!s.empty()) {r[k]=s.top();} else r[k] = n;
            s.push(k);
        }
        // for(int k  = 0;k<n;k++) printf("%d ",r[k]);
        build(1,n,1,pretree);
        build(1,n,1,suftree);
        //建立线段树
        for(int k = 0;k<n;k++)
        {
            update(k+1,suf[k],1,n,1,suftree);
            update(k+1,pre[k],1,n,1,pretree);
        }
        bool f = true;
        for(int k = 0;k< n;k++)
        {
            int l_ = l[k] + 1,r_  = r[k] - 1;
            ll tmp = LONG_LONG_MIN;
            if(r_ >= k + 1) tmp = max(tmp,query(k+2,r_+1,1,n,1,pretree));
            ll pre_; if(k-1>=0) pre_= pre[k-1]; else pre_ = 0;
            if(tmp != LONG_LONG_MIN && tmp - pre_ > a[k]) {f = false;break;}
            tmp = LONG_LONG_MIN;
            if(k-1>=l_) tmp = max(tmp,query(l_+1,k,1,n,1,suftree));
            ll suf_; if(k+1<n) suf_ = suf[k+1]; else suf_ = 0;
            if(tmp!=LONG_LONG_MIN && tmp - suf_ > a[k]) {f =  false;break;}
        }
        if(!f) printf("NO\n"); else printf("YES\n");
    }
    system("pause");
    return 0;
}

Price Maximization(1500 GOOD)

题目大意：给定含n个整数(n为偶数)的数组a,给定一个整数k。将a中元素两个分为一组(记作 $a_i,a_j$ ),求使得 $\lfloor \frac{a_i+a_j}{k} \rfloor$ 总和最大的分组方案对应的总和。
思路：
$\lfloor \frac{a_i+a_j}{k} \rfloor = \frac{a_i + a_j - (a_i + a_j)\%k}{k}$ 且等式右侧分子是k的倍数。于是总和为：
$\sum_{i,j} \frac{a_i + a_j - (a_i + a_j)\%k}{k} = \frac{\sum_i a_i - \sum_{i,j}(a_i + a_j)\% k}{k} \quad \Delta$
而 $a_i + a_j) \% k = (a_i \% k + a_j \% k) \% k$ 。而 $a_i \% k \in [0,k-1]$ 同理对 $a_j$ .于是当 $a_i \% k + a_j \% k \geq k$ 时， $a_i + a_j) \% k = (a_i \% k + a_j \% k) \% k = a_i \% k + a_j \% k - k$ ,否则 $a_i + a_j) \% k = (a_i \% k + a_j \% k) \% k = a_i \% k + a_j \% k$ 。由 $\Delta$ 式的形式可知要使得 $a_i \%k + a_j \%k \geq k$ 的配对数尽可能多。设数组b满足 $b_i = a_i \% k$ ，将b排序。采用双指针贪心。l最初指向b第一个,r最初指向b的最后一个。l不断增加到第一个使得 $\geq k$ 的为止，计数器加1。然后l++,r–,递归进行下一轮匹配。由于最初r指向最大值,因此首轮迭代l不停止的地方的元素一定不能和其余任何元素构成和大于等于k的对。容易证明一定存在最优解存在第一轮迭代得出的对。并且最优子结构显然成立。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main()
{
    int t;
    scanf("%d",&t);
    for(int i = 0;i<t;i++)
    {
        int n; scanf("%d",&n);
        int k; scanf("%d",&k);
        int a[n];
        int b[n];
        ll sum = 0,sum_ = 0;
        for(int q = 0;q<n;q++) {scanf("%d",&a[q]); sum += (ll)a[q]; b[q] = a[q]%k;sum_ += b[q];}
        sort(b,b+n);
        int l   =   0,r  = n - 1,u = 0;
        while(l < r)
        {
            while(l<r && b[l] + b[r] < k) l++;
            if(l < r) u++;
            l++; r--;
        }
        cout << (sum - (ll)(sum_ - u * k)) / k << endl;
    }
    system("pause");
    return 0;
}

Difference Array（1900）

题目大意：给定升序数组a,求其差分数组 $b_{i+1} - b_i$ ，然后将该差分数组升序排列生成一个新的数组，不断重复此过程直到仅剩下一个元素。问仅剩下的元素等于多少。
数据范围： 原始a的最大值不超 $5e^5$ ，n不超过 $2.5 \cdot 10^5$
参考那个codeforce等差数列公差的题
这里借鉴了知乎大佬的做法
直观来看，给定a的和范围较小，则差分数组中可能取值较少。则利用map维护相同的差分取值。
下面给出严格证明：（参考了知乎）
关键是，在值域一定(设最大值为n)的非负升序排列的数组中，对应差分数值可能取值个数 $O(\sqrt{n})$ 。因为在升序排好的数组中，差小于 $\sqrt{n}$ 的相邻两个数自然不考虑。但差大于 $\sqrt{n}$ 的相邻两个自然数对至多 $\sqrt{n}$ 个(数对的限制造成差分取值的限制),否则值域超过n。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll d[9500000];


void solve(map<int,int>& q)
{
    map<int,int> m;
    for(auto iter = q.begin();iter!=q.end();iter++)
    {
       if(iter->second > 1) m[0]+=(iter->second - 1);
       auto temp = iter; temp++;
       if(temp!=q.end()) {m[temp->first - iter->first]++;}
    }
    q = m;
}


int main()
{
    int t; scanf("%d",&t);
    for(int i = 0;i<t;i++)
    {
        int n;
        scanf("%d",&n);
        int a[n];
        map<int,int> q;
        for(int k  = 0;k<n;k++) {scanf("%d",&a[k]);}
        for(int k = 0;k<n-1;k++) {q[a[k+1]-a[k]]++;}
        for(int i = 0;i<n-2;i++) {solve(q);}
        printf("%d\n",(*q.begin()).first);
    }
    system("pause");
    return 0;
}

Lena and Matrix(1900 GOOD)

题意：二维n*m矩阵上格点要么为白色，要么为黑色。找一个格点使其到所有黑色格点的汉明距离的最大值最小。其中 $n\times m <1e^6$
题解：
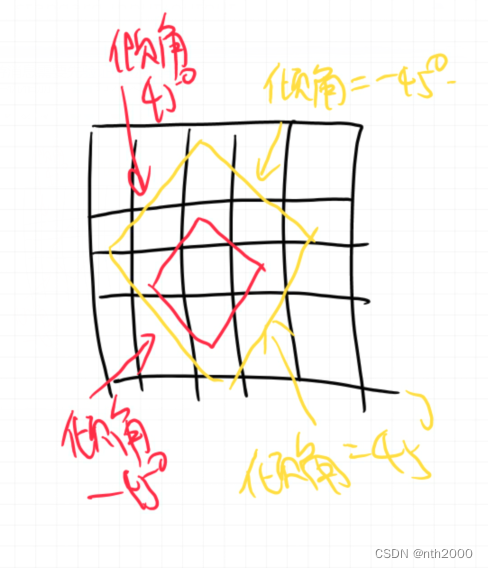在这里插入图片描述距离某格点汉明距离相同的点集合为如图4条线段其中2条倾斜角为45度，另外两条倾斜角-45度，随着汉明距离增大这几条线段作为直线逐渐向外扩充。将4条直线分别平移到最边界的黑色格点，这几个黑色格点距离中心的汉明距离分别大于等于直线本身平移的距离（画一下很容易知道），而直线又确实平移到了边界，因此针对原矩阵每个格点只有这几个边界黑色格点才可能距离其自身最近。倾斜角45度和-45度对应格点的i+j和i-j是定值且为截距,因此找i+j和i-j的最大值和最小值就是这4条直线的截距了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;



int main()
{
    int t;
    scanf("%d",&t);
    for(int o = 0;o<t;o++)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        int maxjpi = INT_MIN,maxjmi = INT_MIN;
        int minjpi = INT_MAX,minjmi = INT_MAX;
        getchar();
        for(int i  = 1;i<=n;i++)
        { 
        for(int j  = 1;j<=m;j++)
        {
            char ch; scanf("%c",&ch); 
            if(ch == 'B')
            {
                maxjpi = max(j+i,maxjpi);
                maxjmi = max(j-i,maxjmi);
                minjpi = min(j+i,minjpi);
                minjmi = min(j-i,minjmi);
            }
        }
           getchar(); }
        int ans = INT_MAX;  
        int min_a = 1;
        int min_b = 1;
        for(int i = 1;i<=n;i++) for(int j  = 1;j<=m;j++)
        {
            int a = max(abs(maxjpi - (i + j)),abs(minjpi-(i+j)));
            int b = max(abs(maxjmi - (j - i)),abs(minjmi-(j - i)));
            if(max(a,b) < ans)
            {
                ans = max(a,b);
                min_a = i; min_b = j;
            }
        }
        printf("%d %d\n",min_a,min_b);
        
    }
    system("pause");
    return 0;
}

Palindrome Basis

题意： 给定整数n有多少种将其分为回文数的不同方案。其中 $\leq 4e^4$ 。两个方案不同当且仅当它们至少有一个数不同，或长度不同，即是不同的multiset。
解答：
显然先预处理所有回文数
我的方法是计算dp[i][k]，意义为将i分为回文数其中第一个数为k的非递减方案数量。对每个i再维护一个dp[i]的前缀和。这种方法解空间划分不太恰当

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;




int main()
{
    vector<int> p;
    for(int i  = 1;i<=40000;i++)
    {
        vector<int> a;
        int j  = i;
        while(j > 0) {a.push_back(j%10); j/=10;}
        int l  = 0,r = a.size() - 1; bool f = true;
        while(l <= r){if(a[l]!=a[r]){f = false;break;} else {l++;r--;}}
        if(f) p.push_back(i);
    }
    vector<ll> dp[40001];
    vector<ll> pre[40001]; 
    for(int i = 1;i<40001;i++)
    {
        //枚举第一个数字
        int q = 0; 
        while(q < p.size() && p[q] <= i) 
        {
            if(q - 1 < (ll)pre[i - p[q]].size() - 1)
            {
                ll b; if(q-1<0) b=0; else b = pre[i - p[q]][q - 1];
                dp[i].push_back((pre[i - p[q]][pre[i - p[q]].size() - 1] - b + mod) % mod);
            }
            else if(p[q]!=i)dp[i].push_back(0);
            if(p[q] == i) {dp[i].push_back(1);}
            q++;
        }
        ll pre_ = 0; 
        for(int k  = 0;k<dp[i].size();k++) {pre[i].push_back((pre_ + dp[i][k])%mod);pre_ = pre[i][k];}
        // for(int k  = 0;k<pre[i].size();k++)
        // {
        //     cout << pre[i][k] << endl;
        // }
    }
    int t;scanf("%d",&t);
    for(int i = 0;i<t;i++) {int n; scanf("%d",&n);printf("%d\n",pre[n][pre[n].size() - 1]);}
    system("pause");
    return 0;
}

事实上，该题是经典的完全背包问题。动态规划中只需要猜测一个回文数是否需要使用从而划分解空间
设 $d p [i] [m]$ ,仅使用前m个回文数分别数i的方案总数。根据第m个回文数是否使用：
$d p [i] [m] = d p [i] [m - 1] + d p [i - p [m]] [m]$
右式前半部分为仅用前m-1个回文数的方案
后半部分为至少使用第m个回文数一次的方案数
画出拓扑图，显然可以优化为一维dp

vector<int>v;
int check(int n) {
    int tmp = n,res = 0;
    while (n) {
        res = res * 10 + n % 10;
        n /= 10;
    }
    return res == tmp;
}
int f[MAXN];
void slove() {
    for (int i = 1; i <= 4e4; i++)
        if (check(i))v.push_back(i);
    f[0] = 1;
    for (int x : v) 
        for (int i = 0; i <= 4e4; i++) 
            (f[i + x] += f[i]) %= mod;
    int T; cin >> T; while (T--) {
        int x; cin >> x;
        cout << f[x] << endl;
    }
}

nth2000

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
2022-07-18 至 2022-07-25 记录

从起点到终点走的格点数是固定的，都是n+m-1。因此n+m-1为奇数时，不可能达成目标。而n+m-1为偶数时，由于奇+奇=偶，奇-奇=偶，因此到达(n,m)点的所有路径和都为偶数。这是因为可以移动每次上下水平向右移动的步骤使得路径和变为最大值。给定n*m方阵，每个格点上有1或-1。问是否存在从起始点(1,1)到(n,m)一条和为0的路径。这种思想以前是遇到过的，见那个很妙的滑动窗口均值的题(jujuandbinarystring2800)。，每次移动改变路径和-2或2。...................
复制链接

扫一扫