"汉诺塔"算法-之通俗易懂,简单的原理-java编程

1.初步介绍

   很多朋友向我咨询汉诺塔的执行过程和原理,其实对于汉诺塔问题,如果不采用递归算法,这种问题就会难以解答,那么下面我通过图解和代码统一把过程和原理写出来,并讲解一些技巧,希望能帮组大家完全理解这个过程和原理.

---

2.图解执行过程

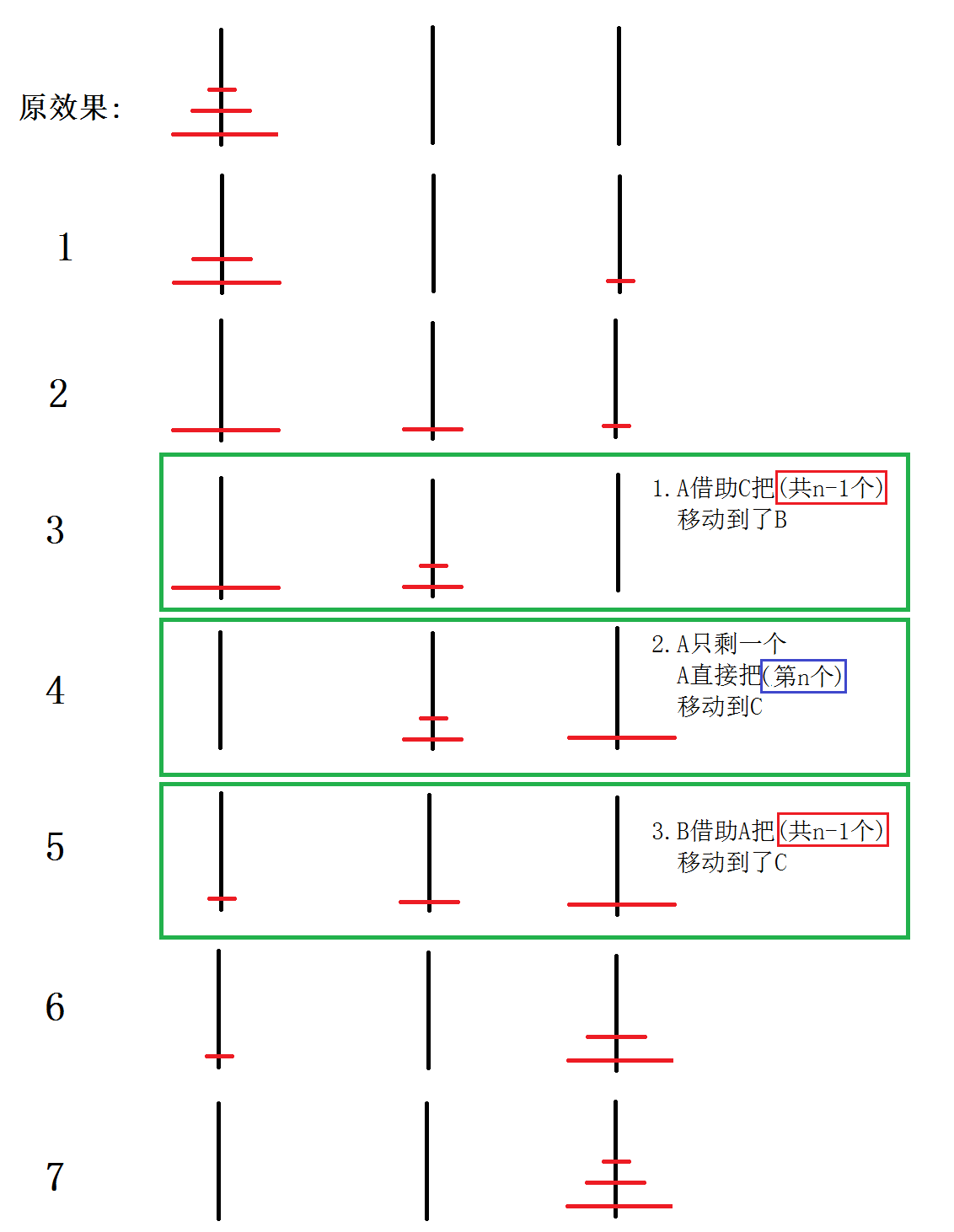
执行过程图:

---

3.特点分析

解决问题的关键,忽略小细节,注重大步骤,这就是递归的精华所在.
解决”三步曲”:

• 1.A柱子把”共n-1”个盘借助C盘移动到B盘,完成一个大过程
• 2.A柱子把剩下的”第n”个盘直接移动到C盘,完成一个大过程
• 3.B柱子上的”共n-1”个盘借助A移动到C盘,又完成一个大过程

这”三步曲”结合递归方法,即可轻松解决问题,以下是给出的详细代码

---

4.详细代码

    /**
         * 汉诺塔(唯有递归才能解决的问题):
         *
         * ABC三个柱子
         * 
         * 1.3个盘片在A柱子(上到下是小盘到大盘)
         * 
         * 2.要求把盘片移动到C柱子
         * 
         * 3.移动过程中,柱子不能出现小盘在下面
         *
         * 4.需求:请列出移动的过程,还有移动的次数;
         *
         * 先分析大过程,忽视细节
         * 
         * 1. A柱子的3个盘子,两个盘子肯定借助C移动到B,完成一个大阶段:
         * 
         * 2. 当A柱子的只剩下最大盘子,那么移动到C
         * 
         * 3. B柱子的两个盘借助A移动到C
         * 
         * 解决的关键是记住大的方向
         */
        public class Demo01 {

            private static int moveCount;

            public static void main(String[] args) {
                getNum(2);
            }

            private static void getNum(int num) {
                char a = 'A';
                char b = 'B';
                char c = 'C';
                moveCount = 0;//计数器
                move(num, a, b, c);
                System.out.println("moveCount = "+moveCount);//打印移动的步骤
            }

            /**
             *
             * @param moveNum
             *            移动的个数
             * @param a
             *            原柱子
             * @param b
             *            辅助柱
             * @param c
             *            目标柱子
             */
            private static void move(int moveNum, char a, char b, char c) {//原->辅助->目标
                moveCount++;
                // 看图:2.只有一个时,A把("第"n)个移动到C
                // 内部: 只有一个时,原柱子->目标柱子
                if (moveNum == 1) {
                    System.out.println("from # " + a + " move " + moveNum + " to " + c);
                } else {
                    // 看图: 1.A借C把("共"n-1个)移动到B
                    // 内部: 多个:原柱子->辅助柱子
                    // C变成辅助,所以排在第二位,B变成目标;
                    move(moveNum - 1, a, c, b);
                    System.out.println("from - " + a + " move " + moveNum + " to " + c);
                    // 看图: 3.B借A把("共"n-1)个移动到C
                    // 内部: 多个:辅助柱->目标柱子
                    // A是辅助,所以排在第二位置,C变目标;
                    move(moveNum - 1, b, a, c);
                }
            }
        }

运行结果:

from  A move 1 to C
from  A move 2 to B
from  C move 1 to B
from  A move 3 to C
from  B move 1 to A
from  B move 2 to C
from  A move 1 to C
moveCount = 7

---

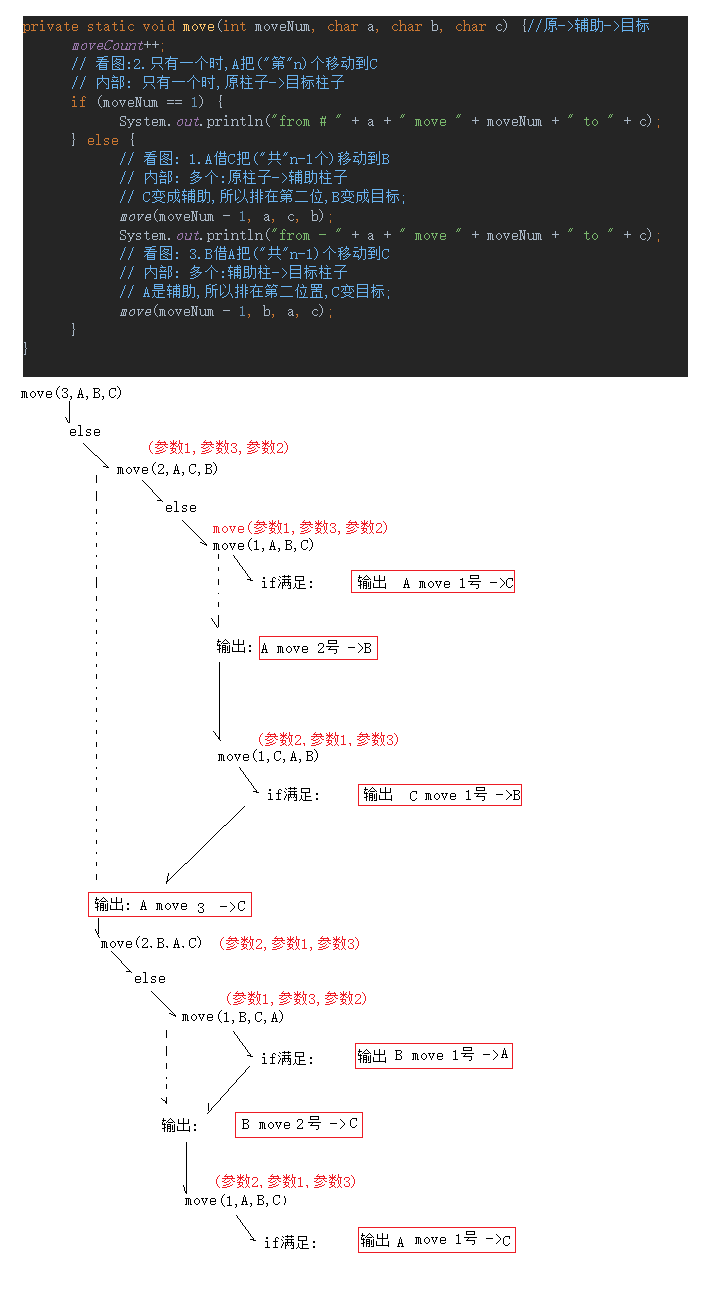
很多朋友还是想让我画出详细的内部图,那么下面我就把完整的代码内部执行流程写出来给大家:

(ps:这里最重要的就是注意参数,考虑内部的时候,不要一直把A就当作原柱子,B当作辅助柱子,C当作目标柱子,而是根据move(n,参数1,参数2,参数3),因为A,C也可以充当辅助柱子,这里固定不变的是:参数1,为原柱子,2为辅助柱,3为目标柱)

---

内部流程图:

---

5.总结

汉诺塔,内部的执行过程是相对繁琐的,所以大家只要记住3个步骤就可以轻松解决并容易记住该算法:

三个柱子:1.原柱子2.中间柱(辅助)3.目标柱
    1.A把"共"n-1个通过C移到B(递归)
    2.如果只剩一个:A把"第"n个直接移动到C盘(打印)
    3.B在通过A把"共"n-1个移到C(递归)

好了,关于汉诺塔的问题就先给大家讲到这里,大家有什么见解请留言相互学习.