
为什么在x1和x2的取值范围相差太大时代价函数的等值图会是一个扁长的椭圆形呢?
这里从代价函数的表达式入手来进行分析。
多元线性回归的代价函数表达式如下:

如果我们将hθ(x)展开,上式就可以写成
在这个表达式中,我们只关注蓝色部分(蓝色部分是变量)
在例子中,我们知道x1和x2的取值范围分别为[0,2000]和[1,5],那么对于等值线图,如果我们任意取一条垂直于θ1轴的直线来看,如下图

由等值线的含义可以知道,上面图中两个相同标记(红色圆圈以及黑色×)的地方其J(θ)的函数值是相同的,然后我们再看下面这张图
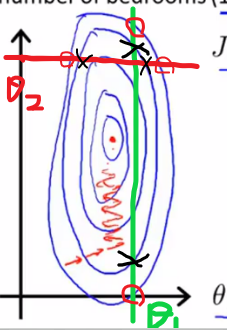
同样地,也做了红色和黑色的标记。而且,上图中的四个红色标记和四个黑色标记的J(θ)值是相同的。
但是我们可以明显看到在θ1方向的变化比在θ2方向的变化小,这时就涉及到了我们上面蓝色的表达式,
因为,x2的取值范围比x1小得多,所以在J(θ)要在两个等值间变化时,对应于x2的参数θ2的变化范围就必须必x1所对应参数θ1的变化范围大得多,来达到平衡这两者之间关系的目的。
所以这个等值线图的形状是一个扁平的椭圆。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








