二叉树-最近公共祖先

问题：给定一棵二叉树，找到两个节点的最近公共父节点(LCA)。最近公共祖先是两个节点的公共的祖先节点且具有最大深度。

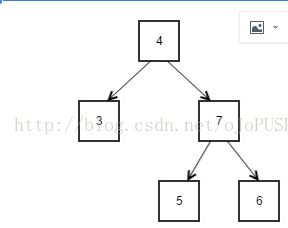
对于上面例子：LCA(3, 5) = 4; LCA(6, 7) = 7

1，a,b位于二叉树根节点的左右子树，则lca为二叉树根节点。否则lca为二叉树左子树（或右子树）节点。

对于1的思路并不能直接转化为代码实现思路。

1.1，因为是找最近公共父节点，所以当前节点符合a或b，则返回当前节点。

当遍历到一个root点的时候，

1，根节点为空，或根节点与目标节点相同，则返回根节点。

2，如果目标节点在根节点的左右子树，那么左右子树递归函数返回值不为空。此时返回根节点。

3，如果目标节点在聚集在左子树（或右子树），那么存在左右子树递归函数返回值必有一为空。此时返回非空节点。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)

{

if(root == NULL || root == p || root ==q) return root;

TreeNode* left = lowestCommonAncestor(root->left, p, q);

TreeNode* right = lowestCommonAncestor(root->right, p, q);

if(left && right){

return root;

}else{

return left == NULL ? right : left;

}

}