本文介绍了图论中的连通性概念，包括无向图的连通性和有向图的强连通与弱连通。此外，还讲解了图的连通分量，即顶点集合内任意顶点彼此可达的子集，并通过实例解析了如何识别连通分量。
图论基础(二)
图的连通性
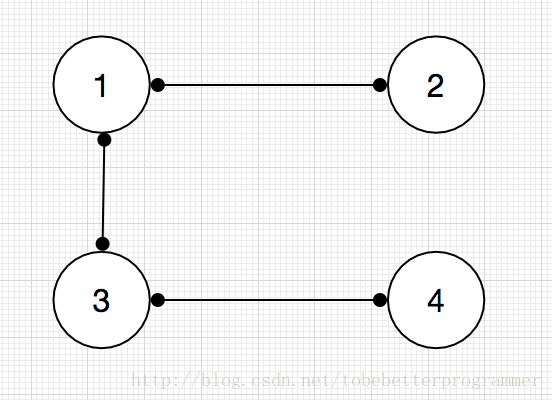
如果无向图G=(V, E)中每一个顶点到其它任意顶点都是可达的，则称G是连通的。假定有无向图G=(V, E)，V={ 1, 2, 3, 4 }，E={ (1, 2), (1, 3), (3, 4) }，则G的结构如下图：
如果有向图G=(V, E)中任意两个顶点互相可达，则称G为强连通图。如果有向图G=(V, E)不是强连通图，但将G中的边去掉方向之后，是一个连通的无向图，则称G为弱连通图。假定有有向图G=(V, E)，V={ 1, 2, 3 }，E={ < 1, 2 >, < 1, 3 >, < 2, 1 >, < 2, 3 >, < 3, 1 >, < 3, 2 > }，则G的结构如下图：
最低0.47元/天 解锁文章
扫一扫
5314
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
