大数据工作流任务调度--有向无环图(DAG)之拓扑排序

拓扑排序(Topological Sorting)

回顾基础知识：

1、图的遍历：
图的遍历是指从图中的某一个顶点出发，按照某种搜索方法沿着图中的边对图中的所有顶点访问一次且仅访问一次。注意树是一种特殊的图，所以树的遍历实际上也可以看作是一种特殊的图的遍历。
2、图的遍历主要有两种算法：广度优先搜索（Breadth First Search，BFS）和深度优先搜索（Depth First Search，DFS）。

• [1] 深度优先搜索(DFS)
  深度优先搜索的搜索策略是尽可能深地搜索一个图。基本思想是：首先访问图中某一未访问的顶点V1，然后由V1出发，访问与V1邻接且未被访问的任一顶点V2，再访问与V2邻接且未被访问的任一顶点V3，……重复上述过程。当不能再继续向下访问(即孤立点)时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止。

• [2] 广度优先搜索(BFS)
  广度优先搜索的基本思想是：首先访问起始顶点v，接着由v出发，依次访问v的各个未访问过的邻接顶点w1，w2，…，wi，然后再依次访问w1，w2，…，wi的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，再访问它们所有未被访问过的邻接顶点……依次类推，直到图中所有顶点都被访问过为止。
  举例说明：
  
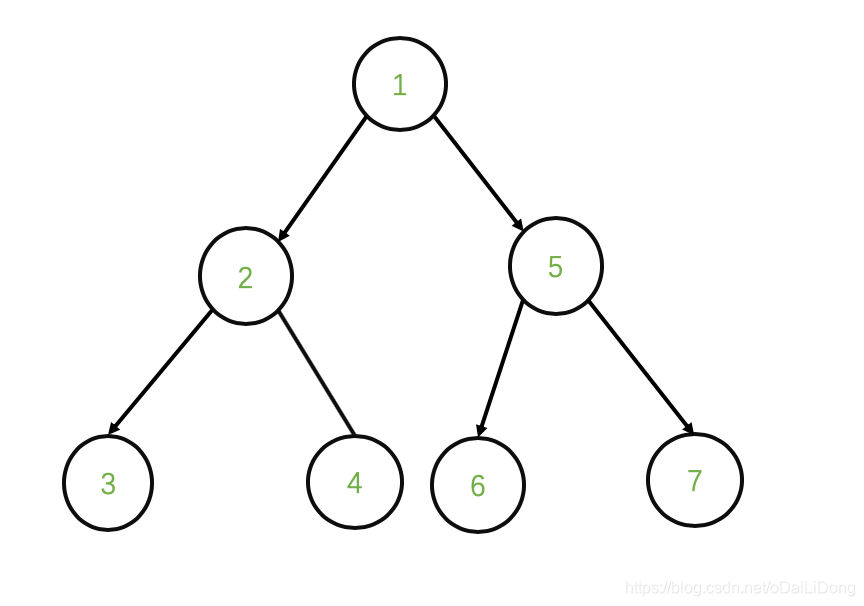
  其BFS遍历如下：1 2 5 3 4 6 7
  其DFS遍历如下：1 2 3 4 5 6 7

接下来说正题：

维基百科上拓扑排序的定义为:

对于任何有向无环图(Directed Acyclic Graph，DAG)而言，其拓扑排序为其所有结点的一个线性排序(同一个有向图可能存在多个这样的结点排序)。该排序满足这样的条件——对于图中的任意两个结点U和V，若存在一条有向边从U指向V，则在拓扑排序中U一定出现在V前面。

通俗来讲：拓扑排序是一个有向无环图(DAG)的所有顶点的线性序列, 该序列必须满足两个条件：

• 每个顶点出现且只出现一次。
• 若存在一条从顶点A到顶点B的路径，那么在序列中顶点 A出现在顶点 B的前面。

如何找出它的拓扑排序呢？这里说一种比较常用的方法：

1. 从DAG图中选择一个入度为0的顶点并输出。
2. 从图中删除该顶点和所有以它为起点的有向边。
3. 重复1和2直到当前的DAG图为空或当前图中不存在入度为0的顶点为止。后一种情况说明有向图中必然存在环。

穿插一下：有向图结点的入度(indegree)和出度(outdegree)的概念。
假设有向图中不存在起点和终点为同一结点的有向边。
入度：设有向图中有一结点V，其入度即为当前所有从其他结点出发，终点为V的的边的数目。也就是所有指向V的有向边的数目。
出度：设有向图中有一结点V，其出度即为当前所有起点为V，指向其他结点的边的数目。也就是所有由V发出的边的数目。

例如下面这个DAG图：

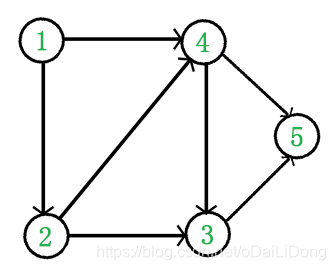
结点1的入度：0，出度：2
结点2的入度：1，出度：2
结点3的入度：2，出度：1
结点4的入度：2，出度：2
结点5的入度：2，出度：0

它的拓扑排序流程为：

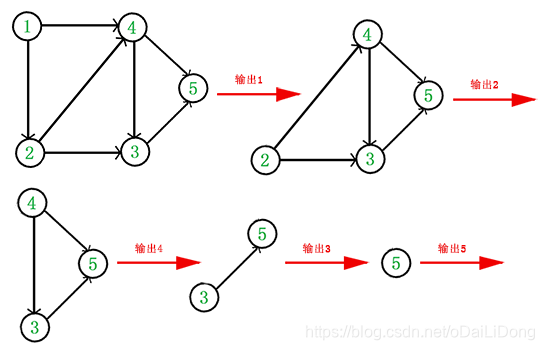
于是，得到拓扑排序后的结果是: {1,2,4,3,5} 。
如果没有结点2 —> 结点4的这个箭头，那么如下：

我们可以得到它的拓扑排序为：{1,2,4,3,5} 或者 {1,4,2,3,5} ，即对同一DAG图来说，它的拓扑排序结果可能存在多个

拓扑排序主要用来解决有向图中的依赖问题。

在讲到实现的时候，有必要插以下内容：

由此我们可以进一步得出一个改进的深度优先遍历或广度优先遍历算法来完成拓扑排序。以广度优先遍历为例，这一改进后的算法与普通的广度优先遍历唯一的区别在于我们应当保存每一个结点对应的入度，并在遍历的每一层选取入度为0的结点开始遍历（而普通的广度优先遍历则无此限制，可以从该吃呢个任意一个结点开始遍历）。这个算法描述如下：

初始化一个Map或者类似数据结构来保存每一个结点的入度。
对于图中的每一个结点的子结点，将其子结点的入度加1。
选取入度为0的任意一个结点开始遍历，并将该节点加入输出。
对于遍历过的每个结点，更新其子结点的入度：将子结点的入度减1。
重复步骤3，直到遍历完所有的结点。
如果无法遍历完所有的结点，则意味着当前的图不是有向无环图。不存在拓扑排序。

广度优先遍历拓扑排序的核心Java代码如下：

public class TopologicalSort {
  /**
   * 判断是否有环及拓扑排序结果
   *
   * 有向无环图(DAG)才有拓扑(topological)排序
   * 广度优先遍历的主要做法：
   *    1、遍历图中所有的顶点，将入度为0的顶点入队列。
   *    2、从队列中poll出一个顶点，更新该顶点的邻接点的入度(减1)，如果邻接点的入度减1之后等于0，则将该邻接点入队列。
   *    3、一直执行第2步，直到队列为空。
   * 如果无法遍历完所有的结点，则意味着当前的图不是有向无环图。不存在拓扑排序。
   *
   *
   * @return key返回的是状态, 如果成功(无环)为true, 失败则有环， value为拓扑排序结果(可能是其中一种)
   */
  private Map.Entry<Boolean, List<Vertex>> topologicalSort() {
	//入度为0的结点队列
    Queue<Vertex> zeroIndegreeVertexQueue = new LinkedList<>();
    //保存结果
    List<Vertex> topoResultList = new ArrayList<>();
    //保存入度不为0的结点
    Map<Vertex, Integer> notZeroIndegreeVertexMap = new HashMap<>();

    //扫描所有的顶点,将入度为0的顶点入队列
    for (Map.Entry<Vertex, VertexInfo> vertices : verticesMap.entrySet()) {
      Vertex vertex = vertices.getKey();
      int inDegree = getIndegree(vertex);

      if (inDegree == 0) {
        zeroIndegreeVertexQueue.add(vertex);
        topoResultList.add(vertex);
      } else {
        notZeroIndegreeVertexMap.put(vertex, inDegree);
      }
    }
    
	//扫描完后，没有入度为0的结点，说明有环，直接返回
    if(zeroIndegreeVertexQueue.isEmpty()){
      return new AbstractMap.SimpleEntry(false, topoResultList);
    }

    //采用topology算法, 删除入度为0的结点和它的关联边
    while (!zeroIndegreeVertexQueue.isEmpty()) {
      Vertex v = zeroIndegreeVertexQueue.poll();
      //得到相邻结点
      Set<Vertex> subsequentNodes = getSubsequentNodes(v);

      for (Vertex subsequentVertex : subsequentNodes) {

        Integer degree = notZeroIndegreeVertexMap.get(subsequentVertex);

        if(--degree == 0){
          topoResultList.add(subsequentVertex);
          zeroIndegreeVertexQueue.add(subsequentVertex);
          notZeroIndegreeVertexMap.remove(subsequentVertex);
        }else{
          notZeroIndegreeVertexMap.put(subsequentVertex, degree);
        }

      }
    }

    //notZeroIndegreeVertexMap如果为空, 表示没有环
    AbstractMap.SimpleEntry resultMap = new AbstractMap.SimpleEntry(notZeroIndegreeVertexMap.size() == 0 , topoResultList);
    return resultMap;

  }
}

注意输出结果是该图的拓扑排序序列之一。
每次在入度为0的集合中取顶点，并没有特殊的取出规则，取顶点的顺序不同会得到不同的拓扑排序序列(如果该图有多种排序序列)。

由于输出每个顶点的同时还要删除以它为起点的边。如果图有V个顶点，E条边，则一般该算法的时间复杂度为O(V+E)。这里实现的算法最终key返回的是状态, 如果成功(无环)为true, 失败则有环， 无环时value为拓扑排序结果(可能是其中一种)。