如何判断一个角是否大于180度？

一。背景

首先，这是一个在特定场景下才会遇到的问题。比如图1中的红弧角，粗略地说，我就是想判断一个多边形（轮廓）的内角是否会有大于180度的情况。

图1

既然是求角，只要3个点的坐标，就能求了啊，如图2，还是红弧角。可以直接上向量点积公式吗？

图2

 

即如下公式：

那肯定是不行：

1)由点积公式算角的余弦，然后试图通过反余弦求角的话，图2中的红角和绿色的余弦是一样的，而且反余弦函数的值域是0到PI。

2)最关键的问题是，点积公式从其本质含义上来说，它就是用来求绿色的（即小于180度的角），该公式的推导可以看我的另一篇博客：https://blog.csdn.net/ogebgvictor/article/details/129103852

 简单地说点积公式中的两个向量，不分先后。但如果我们想求红角的话，这两条边是分先后的！

二。定义

我们现在定义一个特殊的角，就叫大角（即可以大于180度的角），还是参考图2，大角CBA就是红角，大角ABC是绿角，为啥呢，因为我们定的规则是：大角CBA即由BC这边条逆时针旋转到BA所经过的角，自然就是红角了。大角ABC同理，就是BA逆时针旋转到BC所经过的角。

现在把这个规则用在图1的场景中，看看是否适合，如图3，在处理轮廓的时候，肯定是按一个顺序来遍历轮廓上的点，比如就按逆时针遍历轮廓，所以点是有先后顺序的，遍历到点B的时候，我们知道在点B之前先遍历的是A，在点B之后将遍历的是C，所以B点的内角，就是我们定义的大角CBA。

图3

 三。计算方法

 其实计算方法就在我们的定义之中，如图，先把3个点平移一下，使得B点坐标为（0，0），再把BA，BC两边长缩放到1，得到A的坐标为（x2，y2），C的坐标为(x1，y1）。

注：上述操作都不会改变角的大小，另外其实在代码中处理的时候，就是先获取两个向量BC、BA，然后把两个向量归1化就行了。

图4

接下来按照大角的定义，BC要旋转到BA，旋转角为，现在BC、BA的长度都为1了， 所以C点是可以在旋转之后跟A点重合的，所以按照绕原点的旋转公式有：

 接下来就是解方程了：

解出正弦值，求反正弦。但是我们想求的是0到2PI的角，而反正弦的值域是-PI/2到PI/2。

 所以要分4种情况：

1）如果正弦值、余弦值都是正的，那反正弦就是要求的角

 2）如果正弦值是正的，余弦值是负的，则所求角的值是Pi减反正弦。这里画了个箭头，箭头起始处就是反正弦的值，指向处是实际所求的角，它两的平均值是Pi/2，所以它两相加就是Pi喽（同理下不赘述）

 3）如果正弦值是负的，余弦值也是负的，则所求角的值还是Pi减反正弦哦

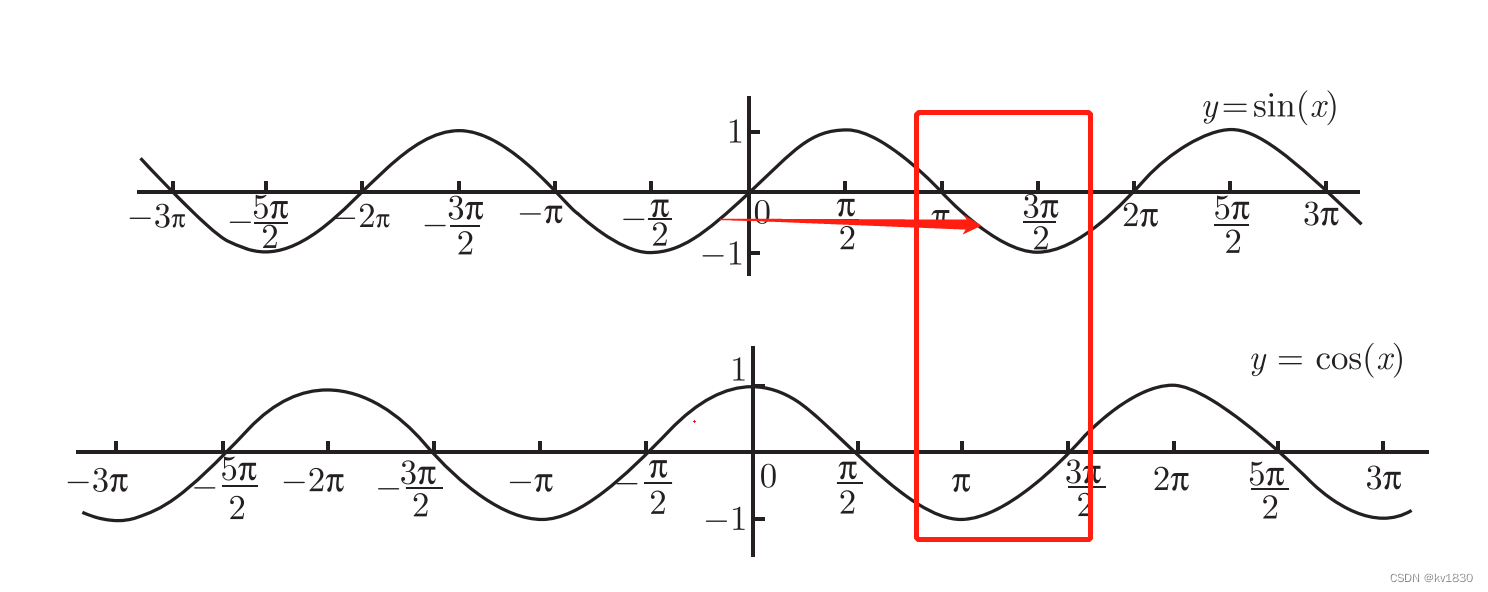
 4)如果正弦值是负的，余弦值是正的，则所求的角的值是反正弦加上2Pi

具体代码下次再补上~~