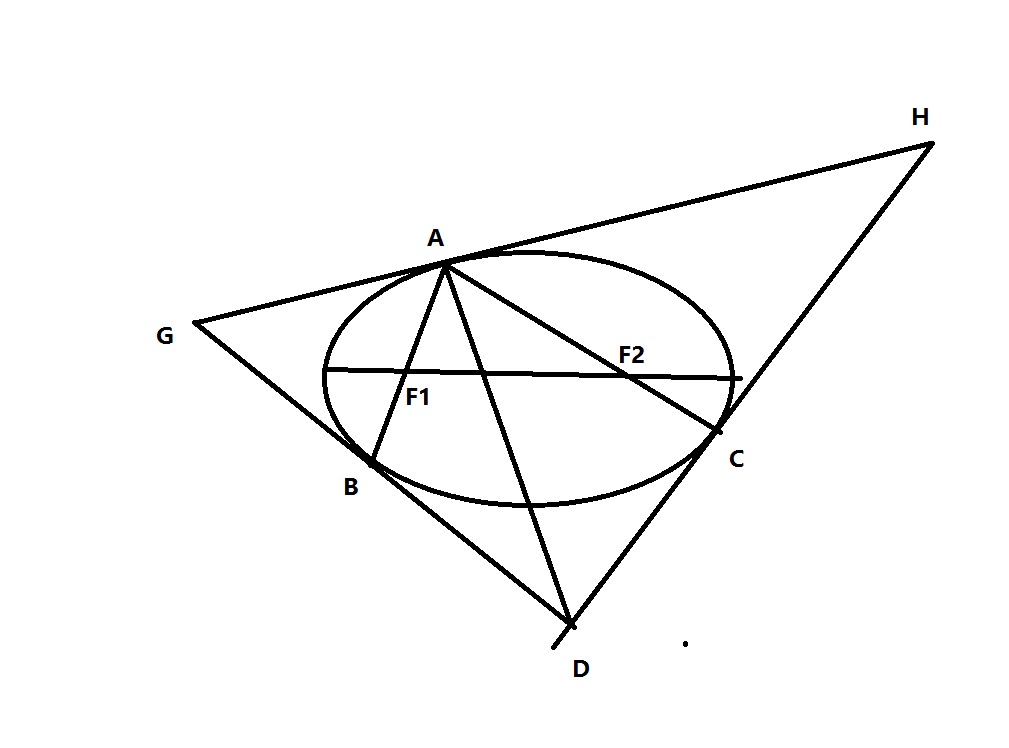
根据二次曲线三角形调和定理
A(BC,GD)=-1
设A点处的切线为GH,法线为AD’
又因为圆锥曲线的光学性质
角BAD'=角CAD'
AD垂直于GH
也就是AD'是角BAC的内角平分线
GH是角BAC的外角平分线
所以A(BC,GD')=-1
所以AD和AD‘重合
既是A点处的法线和B处切线和C处切线三线共点。

根据二次曲线三角形调和定理
A(BC,GD)=-1
设A点处的切线为GH,法线为AD’
又因为圆锥曲线的光学性质
角BAD'=角CAD'
AD垂直于GH
也就是AD'是角BAC的内角平分线
GH是角BAC的外角平分线
所以A(BC,GD')=-1
所以AD和AD‘重合
既是A点处的法线和B处切线和C处切线三线共点。

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


