记录矩阵旋转过程的逻辑

仅用于以文字梳理一遍关于旋转过程中的逻辑。
网上动不动可得，可知。让萌新变得懵逼。所以个人梳理一下，有问题可及时沟通。

旋转一般以矩阵的方式来记录
这里目前只接触了欧拉角矩阵和四元数，其它内容接触到后续更新

欧拉角矩阵的旋转矩阵推导：
推导可以看最近整理的部分：
https://blog.csdn.net/one_day_csdn/article/details/134790732?spm=1001.2014.3001.5502。

这里主要记录一些概念：
多次旋转时，旋转矩阵乘的顺序，也就是我们说的左乘和右乘。
左乘和右乘有时候搞混了，发现算法总是不对。闹心死。

左乘和右乘：

先给出目前总结的结论：
右乘是，按照自身坐标系的旋转
左乘是，固定坐标系的旋转

右乘证明：

假设有3个坐标系a，b，c，a旋转到b，然后再b旋转到c。
a为最初的坐标系
b相对于a的旋转矩阵，记作R_b^a
c相对于b的旋转矩阵，记作R_c^b
c相对于a的旋转矩阵，记作R_c^a
这里的相对于谁，也就是绕哪个坐标系的轴旋转
点M在各个坐标系的坐标为M_a，M_b，M_c。点M的位置没有动，只是坐标系动了。
这里可以得到
M_a = R_b^a * M_b；
M_a = R_c^a * M_c；
M_b = R_c^b * M_c；
上面这个等式应该没问题吧，o(￣▽￣)ブ

简单点说就是
以M_a = R_b^a * M_b为例。
是不是也有人曾经跟我一样，一开始理解成为了M_b = R_b^a * M_a。
a坐标系上的点，M_a旋转之后，得到b坐标系上的点M_b。这么一想还挺合理。
O(∩_∩)O这样是不对的哦。

我们展开讲讲：
我们先需要将b中的坐标点，放到a坐标系中，将坐标系的旋转，转换成为了坐标系a中的点M_b1 （这里是把坐标系做了置换，在b中坐标为M_b那么a中也有一个点M_b 坐标记为M_b1），然后M_b1经过旋转后得到了点M_a 也就是b中的点M_b。
所以M_a = R_b^a * M_b成立。其它等式一个意思

然后三个等式进行代入，
R_b^a * M_b = R_c^a * M_c；
带入M_b
R_b^a * R_c^b * M_c = R_c^a * M_c；
从而知道
R_b^a * R_c^b = R_c^a
这个等式说明了，a旋转到c，等同于a先旋转到b，再旋转到c。

右乘推导成功啦，o(￣▽￣)ブ

左乘证明：

假设有两个坐标系a，b。 a中有两个点M_a和N_a，M和N之间的旋转矩阵是R_n^m 。b中的坐标为M_b和N_b，M和N之间的旋转矩阵是R_nb^mb 。坐标系a和b之间的旋转关系为R_b^a.
则：
M_a = R_n^m N_a
M_a = R_b^aM_b
N_a = R_b^aN_b
将上面的式子做代入
R_b^aM_b = R_n^mR_b^aN_b

又因为M_b= R_nb^mb N_b
所以R_b^a R_nb^mb N_b = R_n^mR_b^aN_b
所以R_b^aR_nb^mbR_a^b = R_n^m
也就是先把坐标系转过去，然后旋转点，然后再把坐标系转回来。

扩展到三个坐标系a，b，c
这里的矩阵R1是为了和之前的相对坐标系移动R区分
坐标系a为固定坐标系
坐标系b相对于a的旋转，旋转矩阵是R1_b^a
坐标系c相对于a的旋转，旋转矩阵是R1_c^a
坐标系c相对于b的旋转，在固定坐标系下旋转矩阵是 R1_c^b

R1_b^a = R_b^a
R1_c^a = R_c^a
R1_c^b = R_b^a * R_c^b * R_a^b
考虑上面右乘时的最终结果公式
R_b^a * R_c^b = R_c^a

所以R1_c^a = R_c^a = R_b^a * R_c^b
又因为R1_c^b = R_b^a * R_c^b * R_a^b得到
R_c^b = R_a^b * R1_c^b * R_b^a
这里是两边同时进行了左乘和右乘消掉了。应该没啥疑问。
所以
R1_c^a = R_b^a * R_a^b * R1_c^b * R_b^a=R1_c^b * R_b^a = R1_c^b * R1_b^a
所以左乘是固定坐标系，推导完成。

至于向量的旋转就不用说了吧。都是左乘。

四元数和旋转矩阵之间的推导

首先，确认绕任意轴旋转的旋转矩阵

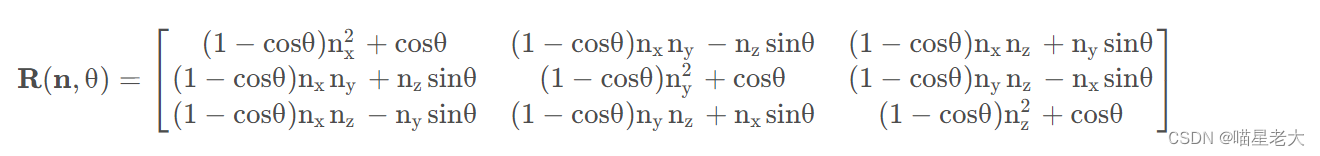
这里是依赖于将旋转的向量，针对于旋转轴切分为水平向量和平行向量，水平的不需要动，而计算垂直的向量的操作
具体可参考https://blog.csdn.net/u014265928/article/details/117170481。
这位解释的很清晰。有疑问大家一起沟通。
这个矩阵用的n和θ表示。
其中四元数和这两个部分的关系是:
w = cos(θ/2);
x = n_xsin(θ/2)
y = n_ysin(θ/2)
z = n_zsin(θ/2)
这个结论是因为q = cos(θ/2) + (xi + yj + z*k)*sin(θ/2) 。这块的半角来源推导还在思考中，待后续理通了更新。
有了这个结论，就可以去求四元数的旋转矩阵模式了。
这里依赖的重要的公式是三角函数倍角公式
cosθ=1−2sin² (θ/2)
sinθ = 2sin(θ/2)cos(θ/2)
将角度用θ转换为θ/2
替换到矩阵中后，就可以得到每个位置依赖于四元数的表现结果。
另外因为x² + y² + z² + w² = 1;对角线部分可以根据需要做替换

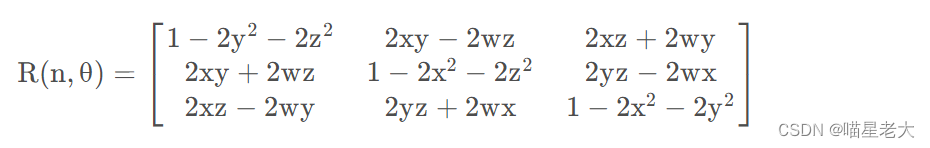
从旋转矩阵到四元数
这个其实我个人认为是一个观察式的结果，O(∩_∩)O。
想到了，就知道了。没想到，就绷不住了。
我们观察上面的四元数旋转矩阵。
对角线相加，会发现，
(1−2y ² −2z ²)+(1−2x ²−2z ² )+(1−2x ²−2y ²)
=3−4(x ²+y ² +z ²)
=3−4(1−w²)
=4w ²−1.
所以我们可以一以此为依据求出来w。
然后想求x，y，z可以通过对角线的三个值进行操作，大家可以试下。
不过这里会出现都是对应值的平方的情况。没有选择正根和负根的依据。

所以我们在求出来，w，x，y，z的其中一项后，可以以它为依据求其它的
​
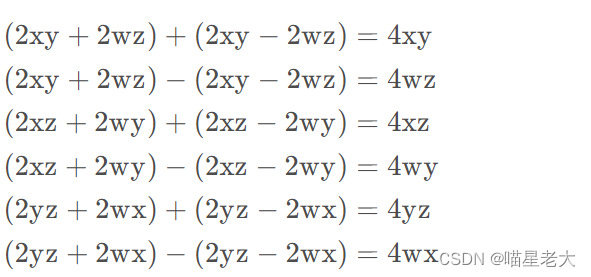
有了四个值中的任意一个，我们就可以把其它三个求出来。