SQUFOF算法解析-CSDN博客

本文链接：https://blog.csdn.net/oqqTZb/article/details/8907627

SQUFOF算法：
参考：维基百科 http://en.wikipedia.org/wiki/SQUFOF#Algorithm

思路：寻找一对整数x和y使其满足x^2=y^2(mod n),此时计算gcd(x-y,n)就会得到n的一个素因子，此时素因子在x和y之间

输入：输入一个n和k，要求n既不是完全平方数也不是素数，k是一个乘数
输出：n的一个素因子

初始化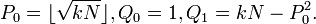： $P_0=\lfloor\sqrt{kN}\rfloor,Q_0=1,Q_1=kN-P_0^2.$

重复执行如下操作：

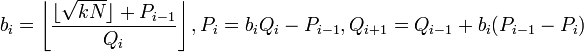
$b_i=\left\lfloor\frac{\lfloor\sqrt{kN}\rfloor+P_{i-1}}{Q_i}\right\rfloor,P_i=b_iQ_i-P_{i-1},Q_{i+1}=Q_{i-1}+b_i(P_{i-1}-P_i)$

直到 $Q_i$ 是完全平方数.

初始化： $b_0=\left\lfloor\frac{\lfloor\sqrt{kN}\rfloor-P_{i-1}}{\sqrt{Q_i}}\right\rfloor,P_0=b_0\sqrt{Q_i}+P_{i-1},Q_0=\sqrt{Q_i},Q_1=\frac{kN-P_0^2}{Q_0}$

注意，此时的i是上一个循环终止时的i值

重复执行如下操作：

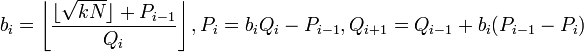
$b_i=\left\lfloor\frac{\lfloor\sqrt{kN}\rfloor+P_{i-1}}{Q_i}\right\rfloor,P_i=b_iQ_i-P_{i-1},Q_{i+1}=Q_{i-1}+b_i(P_{i-1}-P_i)$

直到 $P_{i+1}=P_i.$

T如果 $f=\gcd(N,P_i)$ ！= $1$ || $f=\gcd(N,P_i)$ != $N$ , 此时 $f$ 就是 $N$ 的一个素因子. 否则通过改变 $k$ 的值的大小来做这些操作.

注意，在这儿的 $f=\gcd(N,P_i)$ 中的Pi是最后 $P_{i+1}=P_i.$ 相等时的Pi

一个例子

N = 11111, k = 1

P₀ = 105 Q₀ = 1 Q₁ = 86

P₁ = 67 Q₁ = 86 Q₂ = 77

P₂ = 87 Q₂ = 77 Q₃ = 46

P₃ = 97 Q₃ = 46 Q₄ = 37

P₄ = 88 Q₄ = 37 Q₅ = 91

P₅ = 94 Q₅ = 91 Q₆ = 25

Here Q₆ is a perfect square

P₀ = 104 Q₀ = 5 Q₁ = 59

P₁ = 73 Q₁ = 59 Q₂ = 98

P₂ = 25 Q₂ = 98 Q₃ = 107

P₃ = 82 Q₃ = 107 Q₄ = 41

P₄ = 82

Here P₃ = P₄

gcd(11111, 82) = 41, which is a factor of 11111.

const int maxn=100;

long long gcd(long long a,long long b)
{
    return b==0?a:gcd(b,a%b);
}

long long b[maxn],p[maxn],q[maxn];
long long SQUFOF(long long n,long long k)
{
    long long a=(long long )(sqrt(k*n*1.0));
    long long t;
    int i;
    k=1;
    p[0]=a;
    q[0]=1;
    q[1]=k*n-p[0]*p[0];
    for(i=1;i<maxn;i++)
    {
        b[i]=(long long)((a+p[i-1])/q[i]);
        p[i]=b[i]*q[i]-p[i-1];
        q[i+1]=q[i-1]+b[i]*(p[i-1]-p[i]);
        t=(long long)sqrt(q[i]*1.0);
        if(t*t==q[i])break;
    }
    b[0]=(long long)((a-p[i-1])/t);
    p[0]=b[0]*t+p[i-1];
    q[0]=t;
    q[1]=(k*n-p[0]*p[0])/q[0];
    for(i=1;i<maxn;i++)
    {
        b[i]=(long long)((a+p[i-1])/q[i]);
        p[i]=b[i]*q[i]-p[i-1];
        q[i+1]=q[i-1]+b[i]*(p[i-1]-p[i]);
        if(p[i+1]==p[i])break;
    }
    long long f=gcd(n,p[i]);
    if(f!=1||f!=n)return f;
    else k++;
}