#include <cstdio>
#include <cstring>
#include <iostream>
#define N 251
#define INF 0x0fffffff
using namespace std;
int si,ti,ci;
int V,E,ans;
int dis[N];//记录节点的层次
int map[251][251];
int h,r,q[251]; //储存队列,h为头,r为尾巴
int min2(int x,int y)
{
return x>y?y:x;
}
int dfs_find(int s,int low)
{
if(s==V)
return low;
int a;
for (int i = 1; i <= V; ++i)
{
if(map[s][i]>0&&dis[i]==dis[s]+1&& (a = dfs_find(i,min2(low,map[s][i]))))
{
map[s][i] -=a;
map[i][s] +=a;
return a;
}
}
return 0;
}
int bfs_bulid(int s,int t)
{
memset(dis,0xff,sizeof(dis));//以-1填充
//这个函数是建立网络层次
h=0;r=1;
q[1]=s;dis[s]=0;
while(h<r)
{
int x = q[++h];
for (int i = 1; i <= V; ++i)
{
if(dis[i]==-1&&map[x][i]>0)
{
// printf("%d\n",i);
q[++r]=i;
dis[i] = dis[x]+1;
}
}
}
if(dis[t]>0)
return 1;
else return 0;
}
void dinic(int s,int t)
{
ans = 0;
while(bfs_bulid(s,t))
{
int tts;
while(tts=dfs_find(s,INF))
{
ans+=tts;
//printf("%d\n",tts );
}
}
}
int main(int argc, char const *argv[])
{
while(scanf("%d%d",&E,&V)==2)
{
//int w=0;
memset(map,0,sizeof(map));
for (int i = 1; i <= E; ++i)
{
// printf("%d\n",w++ );
scanf("%d%d%d",&si,&ti,&ci);
map[si][ti] += ci;
}
dinic(1,V);
printf("%d\n",ans);
}
return 0;
}
/*****以下来自<<浅谈基于分层思想的网络流算法>> 王欣*****/
层次图
短路增值算法(MPLA)
算法流程
汇点不在层次图内意味着在剩余图中不存在一条从源点到汇点的路径,即没有增广路。
在程序实现的时候,层次图并不用被“建”出来,我们只需对每个顶点标记层次,增广的时候,判断边是否满足level(u) +1= level(v)这一约束即可。
Dinic算法
Dinic算法的思想也是分阶段地在层次图中增广。
它与最短路径增值算法不同之处是:在Dinic算法中,我们用一个dfs过程代替多次bfs来寻找阻塞流。下面给出其算法步骤:
算法流程
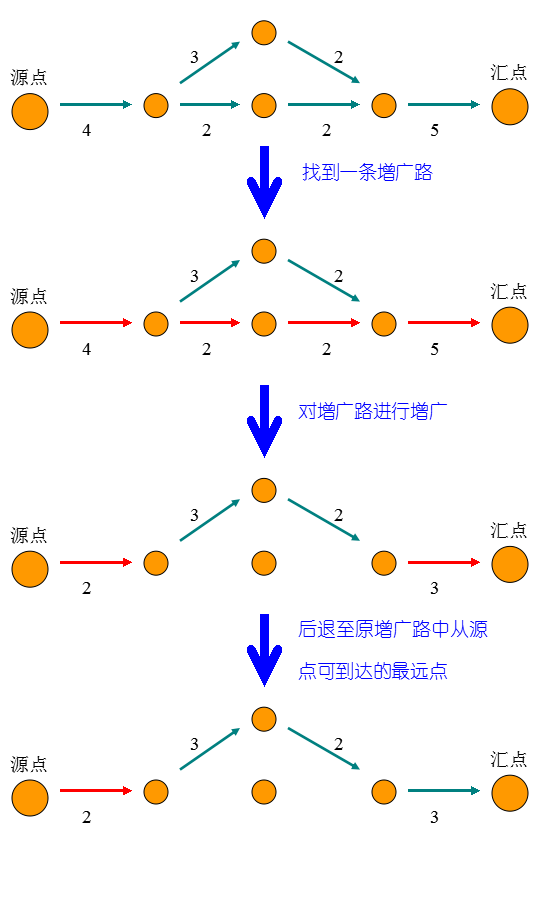
增广过程图解
伪代码描述
在程序里,p表示找到的增广路径,p.top为路径中的最后一个顶点。一开始,p中只有源点。
整个While循环分为2个操作。如果p的最后一个顶点为汇点,也就是说找到了增广路,那么对p增广,注意到增广后一定有一条或多条p中的边被删除了。这时,我们使增广路径后退至p中从源点可到达的最后一个顶点。
如果p的最后一个顶点不为汇点,那么观察最后那个的顶点u 。若在层次图中存在从u连出的一条边,比如(u,v),我们就将顶点v放入路径p中,继续dfs遍历;否则,点u对之后的dfs遍历就没有用了,我们将点u以及层次图中连到u的所有边删除,并且在p中后退一个点。
Dfs过程将会不断重复这2个操作,直到从源点连出的边全部被删除为止。
/*****以上来自<<浅谈基于分层思想的网络流算法>> 王欣*****/








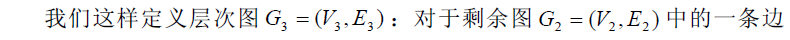




















 1024
1024

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








