奇异分解
假设C是m×n矩阵,U是m×m矩阵,其中U的列为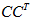
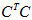
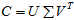
其中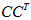
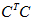
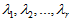
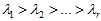
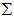
×n的矩阵,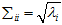
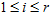
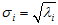
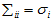
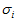
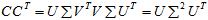
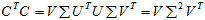
所以有了矩阵C,可以求得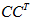
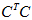
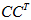
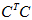
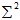
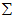
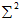
例题:
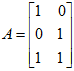
解:
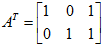
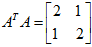
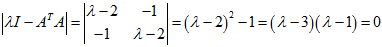
故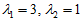
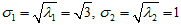
当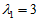
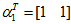
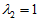
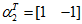
标准化后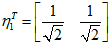
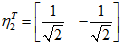
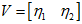
同理,先求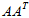
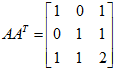
当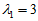
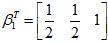
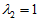
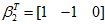
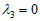
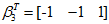
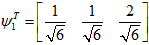
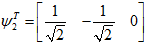
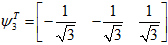
由此可知,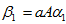
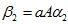
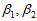
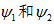
所以
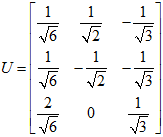
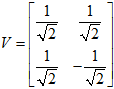
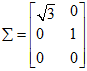
最后得
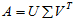
---------------------------------------------------------------------------------
特征值分解——EVD
在这里,选择一种特殊的矩阵——对称阵(酉空间中叫hermite矩阵即厄米阵)。对称阵有一个很优美的性质:它总能相似对角化,对称阵不同特征值对应的特征向量两两正交。一个矩阵能相似对角化即说明其特征子空间即为其列空间,若不能对角化则其特征子空间为列空间的子空间。现在假设存在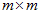
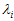
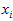
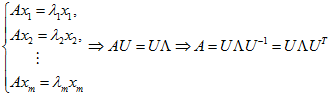
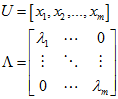
U为的列是两两正交向量,所以它的逆矩阵等于转置矩阵。
奇异值分解——SVD
假设存在一个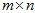
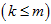
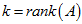
假设这组标准正交基为: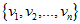
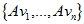
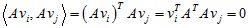
根据假设,也有以下关系: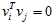
所以如果选择v为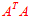
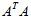
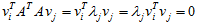
这样就找到了正交基使其映射后还是正交基了,现在,将映射后的正交基单位化:
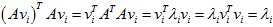
所以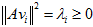
单位化: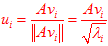
由此得到关系: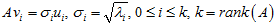
从而得到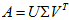
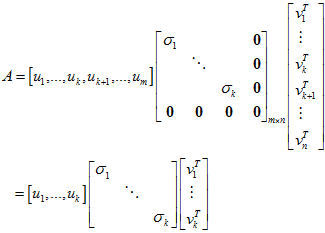
令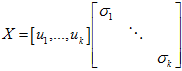
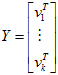
则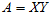
Reference
http://blog.csdn.net/zhongkejingwang/article/details/43053513
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








