【综析】强化学习稀疏奖励算法研究——理论与实验

原创

于 2025-09-18 00:43:55 发布 · 1.7k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #HRL #稀疏奖励

在这里插入图片描述

在强化学习中，奖励 (reward) 起到了引导智能体学习方向的作用[7-8]，缺乏奖励信息将导致智能体学习缓慢甚至无法学习到最优策略，这就是稀疏奖励问题[9](sparse reward problem)。例如，在蒙特祖玛复仇游戏中，玩家需要依次执行上百个动作才能获得奖励，这使其成为了 Atari 游戏中最困难的任务之一[10]。此外，在很多实际任务中，不存在现成的奖励值，人为设计的奖励函数又常常陷入局部最优[11]，这些问题限制了强化学习的实际应用。稀疏奖励问题的研究能够降低奖励函数的设计难度，提高学习算法的样本利用率，加速策略学习的速度，为强化学习的广泛应用与落地打下理论基础[12]。

本文总结了当前主流的稀疏奖励算法，围绕是否引入外部引导信息，将当下主流的稀疏奖励问题解决思路分为两类，分别介绍了奖励塑造[13](reward shaping)、模仿学习[14](imitation learning)、课程学习[15](curriculum learning) 和事后经验回放[11]
(hindsight experience replay)、好奇心驱动[16](curiosity-driven algorithms)、分层强化学习[17](hierarchical reinforcement learning) 等 6 类算法，并在 Mu-joco 的 Fetch Reach 环境[18] 下进行了实验验证和分析，实验代码开源在以下地址
https://github.com/YangRui2015/Sparse-Reward-Algorithms

1 强化学习与稀疏奖励问题数学模型

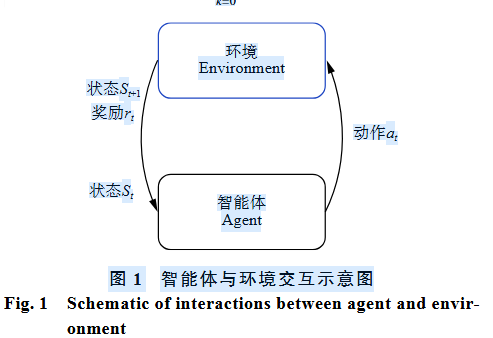
在这里插入图片描述

深度强化学习与传统强化学习的区别是使用了深度神经网络来拟合值函数、策略或环境动态模型[8]。神经网络的引入提高了强化学习解决大规模复杂问题的能力，在众多领域取得了令人瞩目的成绩 [ 1 9 ] 。目前的深度强化学习方法可以分为以下 3 类：基于值函数的方法、基于策略梯度 (policy gradient) 的方法以及 Actor-Critic 的方法[7]。3 类方法的代表分别是 DQN[20-21]、REINFORCE[22]、Actor-Critic[23]，从 Actor-Critic 还衍生出 A3C[24]、PPO[25]、DDPG[26] 等一系列当前主流的强化学习算法。

稀疏奖励的困境

基于值函数的方法，以 DQN[ 20-21] 为例，用代表神经网络的参数，其损失函数为
基于策略梯度的方法，以 REINFORCE[22] 为例，代表神经网络的参数，其更新梯度为

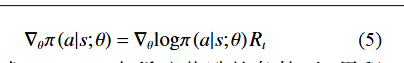
根据式 (1)、(5)，在稀疏奖励的条件下，累积奖励值接近零，因此策略网络更新缓慢。

REINFORCE 是一种无模型（model-free）、**直接优化策略（policy-based）**的强化学习方法。
它通过蒙特卡洛采样（Monte Carlo sampling）估计回报，并使用策略梯度定理来更新策略参数。
核心思想是：增加高回报动作的概率，降低低回报动作的概率。
基于 Actor-Critic[23] 的方法同理，Critic 部分基于值函数更新，Actor 部分基于策略梯度更新，稀疏奖励的条件下两部分梯度更新均接近于零。
稀疏奖励问题除了奖励的稀疏性导致学习缓慢外，还可能存在稀疏性带来的估计不可靠的问题，由于奖励样本少，值函数估计的方差较大，这会导致模型训练难以收敛。

2 稀疏奖励研究现状

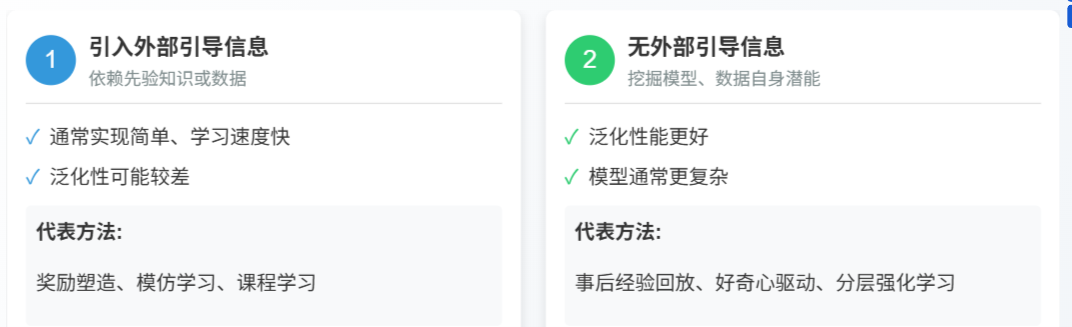
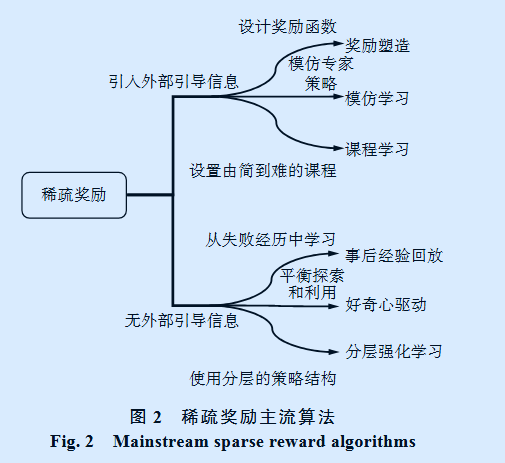
目前解决稀疏奖励问题的算法主要有奖励塑造、模仿学习、课程学习、事后经验回放、好奇心驱动、分层强化学习等 6 类算法，我们可以根据是否引入外部引导信息将算法分为两大类，如图 2所示。

在这里插入图片描述

2.1 奖励塑造

奖励塑造通常是利用先验知识人工设计附加奖励函数[13] 来引导智能体完成期望任务的一类方法。合适的附加奖励函数能够有效克服稀疏奖励问题中奖励的稀疏性，加快智能体学习速度。通常用 $R (s; a; s')$ 表示原 M D P 的奖励函数，用 $F (s; a; s')$ 表示附加奖励函数，使用奖励塑造后新MDP 的奖励函数为

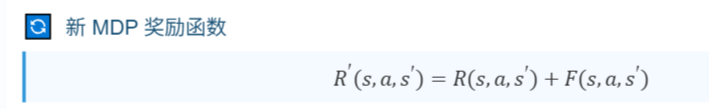
在这里插入图片描述

但是在新的 MDP 问题中学习到的最优策略不一定是原 MDP 的最优策略，也就可能导致奖励塑造后学习到非理论最优的策略[27-28]。Ng 等[27]证明了当附加奖励函数可以表示为势能函数(potiental based funciton) 的差分形式时，能够保证最优策略不变。
在这里插入图片描述

应用示例:

Ng 等人: 使用距离、子目标设计启发式奖励。
Jagodnik 等人: 结合距离信息和人为主观评价控制机器人手臂。
Ferreira 等人: 应用于对话管理任务。

💡用一个简单的例子来说明为什么新的MDP问题中学习到的最优策略不一定是原MDP的最优策略。
假设我们有一个网格世界：

状态：格子位置 .动作：上下左右,左上、左下、右上、右下移动 .原奖励：只在终点获得+1，其他都是0

如果我们随意添加一个附加奖励函数F(s,a,s’)，比如：

每次向上移动给+0.1 ;其他移动给0.

那么新MDP的最优策略可能会变成：总是向上移动，即使这样会绕远路，因为可以获得更多向上移动的奖励。
但原MDP的最优策略应该是：走最短路径到终点，不考虑移动方向。

💡只有当附加奖励是势能函数差分形式时（ $F = γ Φ (s^{'}) - Φ (s)$ ），才能保证新旧MDP的最优策略一致。这个性质由Ng等人在1999年证明.那么势能函数如何设置呢？常见的设计方法有哪些？

基于距离的势能函数

适用场景：目标状态是明确的（如到达某个位置）

设计方法： $\Phi(s) =-dist(s,s_{goal})$ .其中 $dist(s,s_{goal})$ 是状态s到目标状态 $s_{goal}$ 的距离。

案例：在网格世界中，如果目标是 (3,4)，当前状态是 (1,2)。则 $\Phi(s) =-\sqrt{(3-1)^2+(4-2)^2} =-2\sqrt{2}$
s(当前状态) ，s’(下一状态)。假设下一状态s’=(2,3) ,则 $\Phi(s') =-\sqrt{(3-2)^2+(4-3)^2} =-\sqrt{2}$