基于python3的k-means代码实现

k-means算法是非监督学习的一种，其中k值是随机选取的，在本代码中是人为指定为2，准备聚两个类。
算法描述：

1. 加载数据

2. 聚类

2.1、 初始化聚类中心，随机选取两个点作为聚类中心点。

2.2、while直到clusterChanged=false

2.3、计算每个点离中心点的距离，记录最小距离，并标识是属于哪个类。

2.4、更新聚类集合的点。

2.5、 更新聚类中心

代码实现前先浏览一下数据，数据分布如下

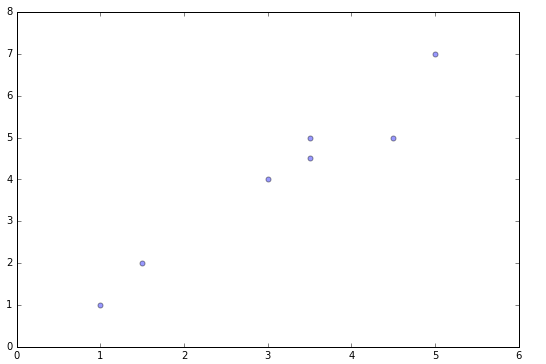
从数据分布可以看出，是7个点。
代码实现分为两个python文件，一个是聚类的实现文件，k_means.py,一个是测试文件test_kmeans.py.
k_means.py如下：

“`# -- coding: utf-8 --
“””
Created on Thu Nov 17 16:13:56 2016

@author: phl
“””
print(“k-means算法程序”)
from numpy import *
import time
import matplotlib.pyplot as plt
def euclDistance(vector1, vector2):
return sqrt(sum(power(vector2 - vector1, 2)))
def initCentriods(dataSet,k):
print(dataSet)
numSamples,dim = dataSet.shape #dim列数
centroids = zeros((k, dim))
print(“行数：”,numSamples)
print(“列数：”,dim)
for i in range(k):
index = int(random.uniform(0, numSamples))
centroids[i, :] = dataSet[index, :]
return centroids
def kmeans(dataSet, k):
numSamples = dataSet.shape[0] #dataSet.shape是几行几列的意思，这里是7行2列
print(“行数：”,numSamples)
clusterAssment = mat(zeros((numSamples, 2)))#初始化一个行两列的0矩阵
clusterChanged = True
## step 1: 初始化聚类中心
centroids = initCentriods(dataSet, k)
print(“随机初始化的两个点：”,centroids)
## 循环遍历数据
while clusterChanged:
clusterChanged = False
for i in range(numSamples):
minDist = 100000.0
minIndex = 0
## 循环遍历中心点
## step 2:计算离中心点的距离
for j in range(k):
distance = euclDistance(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j #minIndex代表类别
##更新聚类分配
if clusterAssment[i,0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist**2
## step 4: 更新聚类中心
for j in range(k):
pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis = 0)
print(‘恭喜你，聚类完成’)
return centroids, clusterAssment
def showCluster(dataSet, k, centroids, clusterAssment):
numSamples, dim = dataSet.shape
if dim != 2:
print(“Sorry! I can not draw because the dimension of your data is not 2!”)
return 1

mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']  
if k > len(mark):  
    print("Sorry! Your k is too large! please contact Zouxy")  
    return 1  

# draw all samples  
for i in range(numSamples):  
    markIndex = int(clusterAssment[i, 0])  
    plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])  

mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']  
# draw the centroids  
for i in range(k):  
    plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12)  
plt.show() 

def showData(dataSet):
x = []
y = []
plt.figure(figsize=(9,6))
for i in dataSet:
x.append([float(i[0])])
y.append([float(i[1])])
plt.scatter(x,y,c=”b”,s=25,alpha=0.4,marker=’o’)
#T:散点的颜色
#s：散点的大小
#alpha:是透明程度
plt.show()

test_kmeans.py如下：
# -- coding: utf-8 --
“””
Created on Thu Nov 17 16:35:03 2016

@author: phl
“””
from numpy import *
import time
import matplotlib.pyplot as plt
from k_means import *
print(“step 1: 加载数据”)
dataSet = []
fileIn = open(‘F:/python/testSet.txt’)
for line in fileIn.readlines():
lineArr = line.strip().split(‘\t’)
dataSet.append([float(lineArr[0]), float(lineArr[1])])
showData(dataSet)
print(“step 2: 聚类”)
dataSet = mat(dataSet) #mat是把数据格式化成列的形式[[1. 1.][1.5 2.][3. 4.][5. 7.]]
k = 2
centroids, clusterAssment = kmeans(dataSet, k)
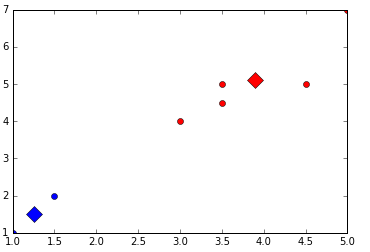
print(“step 3: 展示聚类结果”)
showCluster(dataSet, k, centroids, clusterAssment) “`
结果界面如下：