代码训练营Day.18 | 513. 找树左下角的值、112. 路径总和、106. 从中序与后序遍历序列构造二叉树-CSDN博客

513. 找树左下角的值

1. LeeCode链接

2. 题目描述

3. 解法

1. 迭代法

很简单，层序遍历，找最底层最左边的那个。

class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        queue<TreeNode*> qu;
        qu.push(root);
        int result;
        while (!qu.empty()) {
            int size = qu.size();
            for (int i = 0; i < size; i++) {
                TreeNode* cur = qu.front();
                qu.pop();
                if (i == 0) result = cur->val;
                if (cur->left) qu.push(cur->left);
                if (cur->right) qu.push(cur->right);
            }
        }
        return result;
    }
};

2. 递归法

最终答案满足条件：深度最大的最左叶子节点

因此，1. 从右向左递归，最终值一定被最左叶子节点覆盖；2. 记录叶子节点深度，只选深度最大。

class Solution {
public:
    int result;
    int max_depth = 0;
    void order(TreeNode* root, int depth) {
        if (root == NULL) return;
        depth++;
        if (root->left == NULL && root->right == NULL && depth >= max_depth) {
            max_depth = depth;
            result = root->val;
        }
        order(root->right, depth);
        order(root->left, depth);
    }
    int findBottomLeftValue(TreeNode* root) {
        order(root, 0);
        return result;
    }
};

112. 路径总和

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

3. 解法

用深度递归，当判断为叶子节点，且路径总和等于target时，返回真实路径总和，否则返回不可能是target的值。

class Solution {
public:
    int waySum(TreeNode* root, int sum, int targetSum) {
        if (root == NULL) return 2000;
        sum += root->val;
        if (root->left == NULL && root->right == NULL) {
            if (sum == targetSum) return targetSum;
        }
        if (root->left) {
            int left = waySum(root->left, sum, targetSum);
            if (left == targetSum) return left;
        }
        if (root->right) {
            int right = waySum(root->right, sum, targetSum);
            if (right == targetSum) return right;
        }
        return 2000;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        return targetSum == waySum(root, 0, targetSum) ? true : false;
    }
};

用深度递归，参数量更少的办法是，target可以自顶向下减，而且返回值可以直接是bool型。

class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (root == NULL) return false;
        targetSum -= root->val;
        if (!root->left && !root->right && targetSum == 0) return true;
        return hasPathSum(root->left, targetSum) || hasPathSum(root->right, targetSum);
    }
};

4. 扩展

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

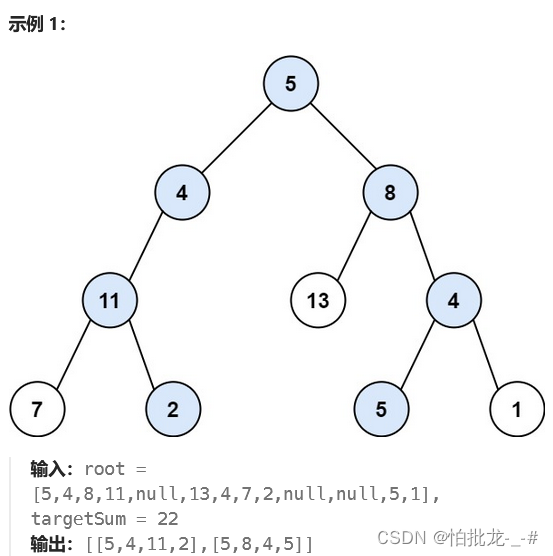
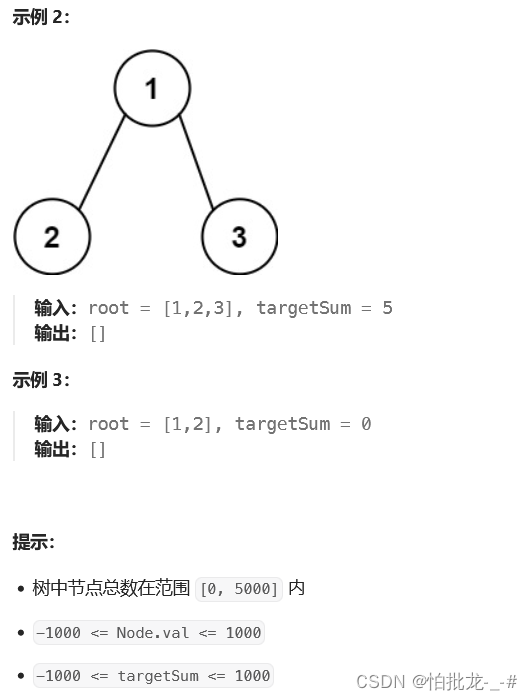
与之前的路径字符串输出一样，也与上题一样，深度递归，新添一个一维vector<int>，如果符合题目，则加入到二维vector<vector<int>>。

class Solution {
public:
    void order(TreeNode* root, int targetSum, vector<int> result, vector<vector<int>>& results) {
        if (root == NULL) return;
        result.push_back(root->val);
        targetSum -= root->val;
        if (!root->left && !root->right && targetSum == 0) results.push_back(result);
        order(root->left, targetSum, result, results);
        order(root->right, targetSum, result, results);
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<vector<int>> results;
        vector<int> result;
        order(root, targetSum, result, results);
        return results;
    }
};

用回溯更快，更省空间。

class Solution {
public:
    vector<vector<int>> results;
    vector<int> result;
    void order(TreeNode* root, int targetSum) {
        if (root == NULL) return;
        result.push_back(root->val);
        targetSum -= root->val;
        if (!root->left && !root->right && targetSum == 0) results.push_back(result);
        if (root->left) {
            order(root->left, targetSum);
            result.pop_back();
        }
        if (root->right) {
            order(root->right, targetSum);
            result.pop_back();
        }
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        order(root, targetSum);
        return results;
    }
};

106. 从中序与后序遍历序列构造二叉树

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

3. 解法

简简单单递归，每次只找当前根节点，而根节点总是在postorder最后一个。然后因为数字不重复，在inorder中找到该根节点后，就可以划分出左右子树的中序遍历和后序遍历。然后继续递归。

class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0) return NULL;
        TreeNode* root = new TreeNode(postorder.back());
        int i = 0;
        for (; i < inorder.size(); i++) {
            if (inorder[i] == postorder.back()) break;
        }
        vector<int> left_in(inorder.begin(), inorder.begin() + i);
        vector<int> right_in(inorder.begin() + i + 1, inorder.end());
        vector<int> left_post(postorder.begin(), postorder.begin() + i);
        vector<int> right_post(postorder.begin() + i, postorder.end() - 1);
        root->left = buildTree(left_in, left_post);
        root->right = buildTree(right_in, right_post);
        return root;
    }
};

4. 扩展

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

前序与中序遍历序列，逻辑跟上面一样，注意切片不要超了。

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0) return NULL;
        TreeNode* root = new TreeNode(preorder[0]);
        int i = 0;
        for (; i < inorder.size(); i++) {
            if (inorder[i] == preorder[0]) break;
        }
        vector<int> left_in(inorder.begin(), inorder.begin() + i);
        vector<int> right_in(inorder.begin() + i + 1, inorder.end());
        vector<int> left_pre(preorder.begin() + 1, preorder.begin() + i + 1);
        vector<int> right_pre(preorder.end() - right_in.size(), preorder.end());
        root->left = buildTree(left_pre, left_in);
        root->right = buildTree(right_pre, right_in);
        return root;
    }
};