小朋友们好,大朋友们好!
我是猫妹,一名爱上Python编程的小学生。
和猫妹学Python,一起趣味学编程。

今日主题
今天是咱们这个有趣的图系列最后一集了,介绍下图的拓扑排序算法。
有趣的图,标题平淡无奇,流量稀稀疏疏,内容却是干货满满。
这些内容啊,或许到了大学我们才会学到,考研或者比赛才需要将其灵活运用,必要的时候需要适度加深。
这属于算法领域,是软件行业中一个重要的分支。

今天要解决的问题是什么呢
假如你穿越到未来,摇身一变,变成了大学教授,要给大学生朋友们排课程表,课程之间呢,有依赖,有些需要先学,有些需要后学。
今有课程间的依赖关系如下,请你来排下课表吧:

这就是生活中的问题,我们首先需要将它转换计算机要解决的问题,然后再利用咱们所学知识将其解决。

图的拓扑排序算法
有向无权图
咱们先用图来表示上述问题,它其实是一个有向无权图。

用临接字典表示有向图
这里的value为key的后续结点,而非后继结点。
如果是后继结点,算法略有差异。

图拓扑排序算法思路
-
先找到一个入度为0的结点,将其先排到课表中。
-
同时上述结点的临接边去掉,也就是解锁和它相邻的结点。
-
如此反复,直到遍历所有结点。
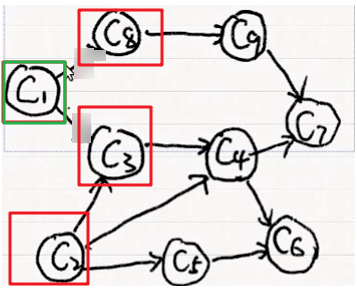
一开始入度为0的结点{C1,C2},可以任选其一,将其排列到课表中,然后解锁和其相邻的结点。

如果我们选的是C1,那么C1已经访问标记下绿色,访问之后的入度为0的结点有{C2,C3,C8}。
再重复类似动作就是了,直到遍历完所有结点。
代码实现(完整代码,见同名公众号,次条推文):

代码逻辑:
13~16行:计算每个结点的入度值
19~24行:依次查找入度为0的结点,每更新一个结点,将其临接结点入度减1,如果入度为0,将其加入队列
25行:i==len(G)表示遍历了所有课程。如果None呢,表示有两门课相互依赖,造成死锁,你依赖我我又依赖你,类似先有鸡还是先有蛋,题目有问题。
运行结果:



好了,我们今天就学到这里吧!
如果遇到什么问题,咱们多多交流,共同解决。
我是猫妹,咱们下次见!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








