有 n 个学生站成一排,每个学生有一个能力值,牛牛想从这 n 个学生中按照顺序选取 k 名学生,要求相邻两个学生的位置编号的差不超过 d,使得这k 个学生的能力值的乘积最大,你能返回最大的乘积吗?
输入描述:
每个输入包含 1 个测试用例。每个测试数据的第一行包含一个整数 n (1 <= n <= 50),表示学生的个数,接下来的一行,包含 n 个整数,按顺序表示每个学生的能力值 ai(-50 <= ai <= 50)。接下来的一行包含两个整数,k 和 d (1 <= k <= 10, 1 <= d <= 50)。
输出描述:
输出一行表示最大的乘积。
示例1
输入
3 7 4 7 2 50
输出
49
一般的动态规划题目,中间使用的表的最后一个元素,dp[N][K]就是所求的结果。但这个题目不能这样,因为如果那样建表,子问题就成了“在前n个学生中,取k个,使乘积最大”——然而,本题目有额外的限制条件“相邻两个学生的位置编号的差不超过d”就没有办法代入递推公式了,因为子问题中本身并不包含位置信息。
因此将子问题定为:在前n个学生中,取k个,第n个必取,使乘积最大。这样的话,最终的结果就不是dp[N][K],而是dp[..][K]这一列中最大的那个值。
其次,求最大乘积比求最大和的问题要复杂许多。求最大和的话,子问题中也只需要求最大和就行了。但求最大乘积的时候,在子问题中,每一步需要求最大正积和最小负积。因为如果某学生的能力值为负数,乘以前面求得的最小负积,结果才是最大乘积。
import java.util.Scanner;
public class HeChangTuan {
public static void main(String[] args) {
//键盘输入
/*
int n=6;
int[] nums={-7,4,5,2,-6,7};
int k=3;
int d=4;
*/
Scanner scan = new Scanner(System.in);
int n = scan.nextInt(); //从键盘输入n值
int[] nums = new int[n];
for(int i = 0; i < n; i++){
nums[i] = scan.nextInt();//从键盘输入能力值
}
int k = scan.nextInt();//从键盘输入选取的人数
int d = scan.nextInt();//从键盘输入误差范围
long[][] max = new long[k][n];
long[][] min = new long[k][n];
for(int i = 0; i < k; i++)
for(int j = 0; j < n; j++){ //给二维数组赋初值
max[i][j] = 1;
if(i == 0){
min[i][j] = nums[j];
max[i][j] = nums[j];
}
// System.out.println("-------------------");
// System.out.println(max[i][j]+" "+min[i][j]);
}
for(int i = 1; i < k; i++)
for(int j = 0; j < n; j++)
for(int m = 1; m <= d; m++){
if(j - m >= 0){
if(nums[j] > 0){
min[i][j] = Math.min(min[i][j], min[i - 1][j - m] * nums[j]);
max[i][j] = Math.max(max[i][j], max[i - 1][j - m] * nums[j]);
} else{
min[i][j] = Math.min(min[i][j], max[i - 1][j - m] * nums[j]);
max[i][j] = Math.max(max[i][j], min[i - 1][j - m] * nums[j]);
}
}
}
long Max = 0;
for(int i = 0; i < n; i++){
//System.out.println(max[k - 1][i]);
//System.out.println(min[k - 1][i]);
Max = Math.max(Max, max[k - 1][i]);
}
System.out.println(Max);
}
}
运行结果为
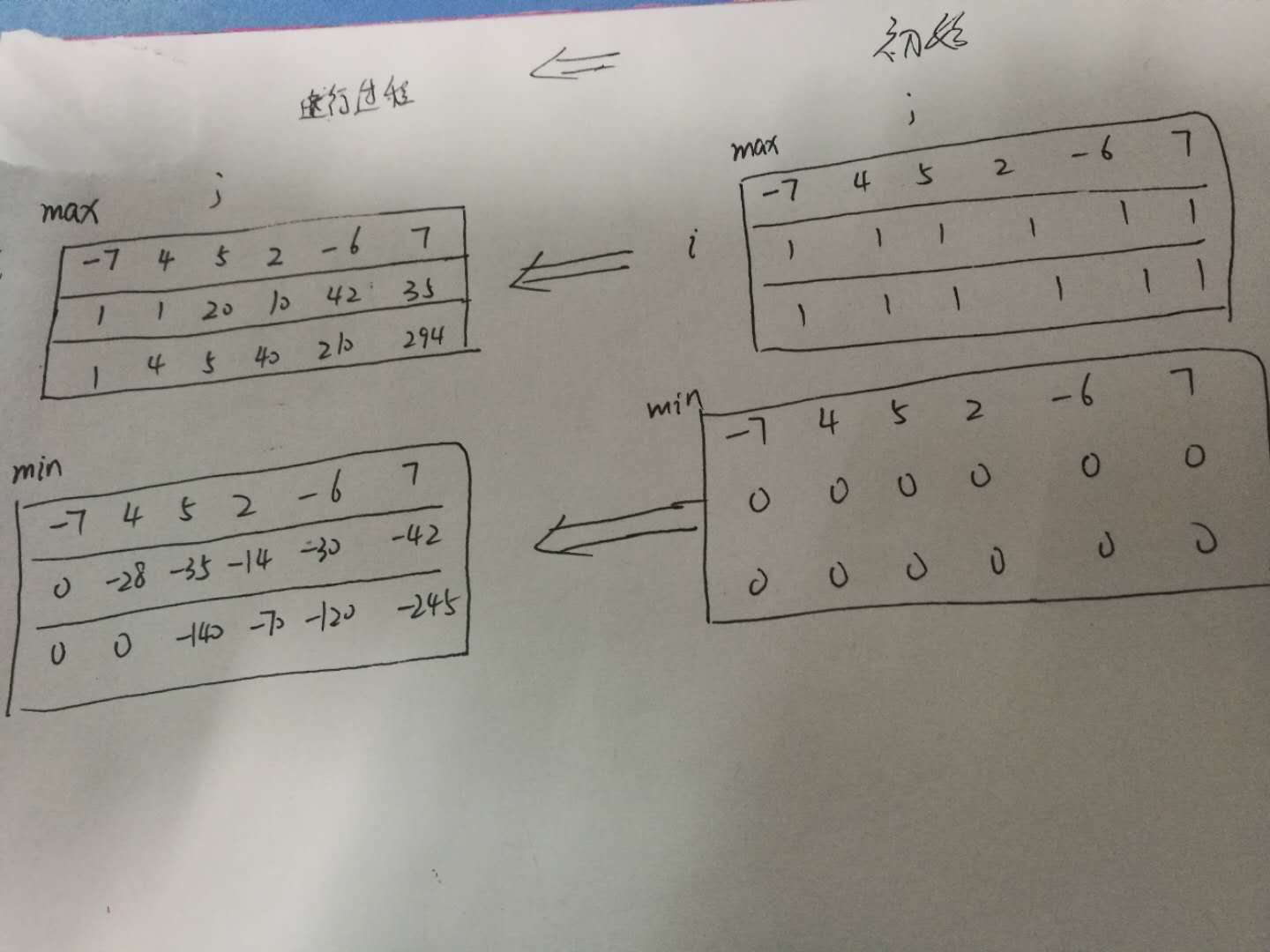
运行过程如下图:
具体步骤:
1、先声明两个两个二维数组max,min
2、对max、min赋初值如上图的右图;
3、在右图中,i控制行数,也即是选择人数;j控制列数,也即是能力值,m控制相邻两数的间距,通过从第一行开始比较,得出的最大值、最小值存到第二行,故i从1开始;
4、对于当前数是正数还是负数分为两种情况。当为正数时,只需要比较当前值与当前值前面的两两乘积,并与1进行比较,选最大的存到当前值下标对应的max表中,同理,最小值也是。公式如下:
min[i][j] = Math.min(min[i][j], max[i - 1][j - m] * nums[j]);max[i][j] = Math.max(max[i][j], min[i - 1][j - m] * nums[j]);
当为负数时,公式如下:
min[i][j] = Math.min(min[i][j], max[i - 1][j - m] * nums[j]);max[i][j] = Math.max(max[i][j], min[i - 1][j - m] * nums[j]);























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








