【自动控制原理】matlab 中零极点分布对三阶控制系统的影响

本文链接：https://blog.csdn.net/persona5joker/article/details/139304290

实验4三阶控制系统的稳定性分析

一、实验目的：

1、通过学习本实验内容，学生能够掌握高阶控制系统时域分析稳定性的方法；

2、了解劳斯稳定判据的应用。

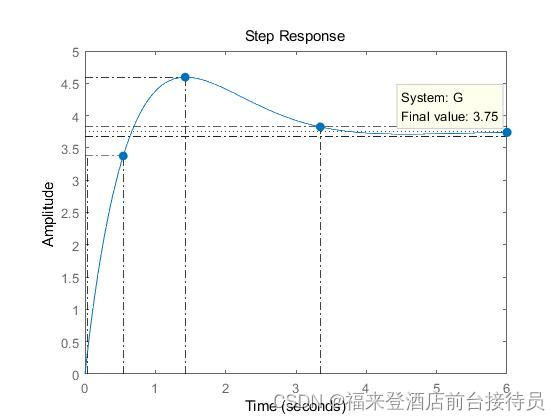
二、实验步骤：

1、已知三阶系统闭环传递函数为Φ（s）＝10(s+1)(s+3)/(s+4)(s^2+2s+2)，

求系统闭环极点及其单位阶跃响应，读取动态性能指标，填入表4-1中。

实验代码：

num=[10,40,30];

den=[1 ,6,10,8];

G=tf(num,den);

p=pole(G)

step(G,6)

代码结果：

p =

-4.0000 + 0.0000i

-1.0000 + 1.0000i

-1.0000 - 1.0000i

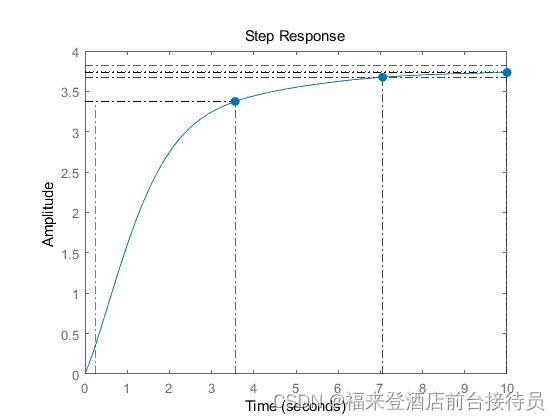
2、改变系统闭环极点的位置，Φ（s）＝1.25(s+1)(s+3) /(s+0.5)(s^2+2s+2)，将原极点s＝-4改成s＝-0.5，使闭环极点靠近虚轴，观察单位阶跃响应和动态性能指标变化。

2实验代码：

num=[1.25,5,3.75];

den=[1 ,2.5,3,1];

G=tf(num,den);

p=pole(G)

step(G,10)

代码结果：

p =

-1.0000 + 1.0000i

-1.0000 - 1.0000i

-0.5000 + 0.0000i

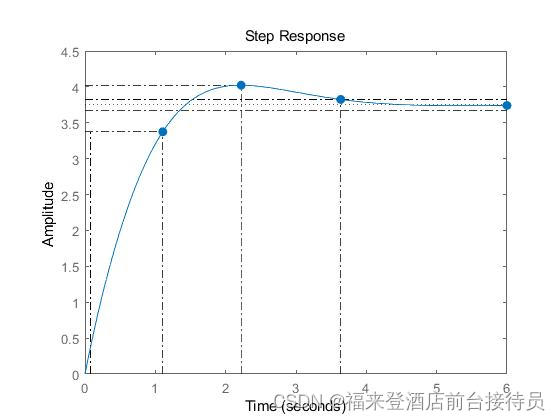
3.改变系统闭环零点的位置，将原零点z=-1改成z=-2，Φ(s)=5(s+2)(s+3)/(s+4)(s^2+2s+2)，观察单位阶跃响应及其动态性能指标的变化。

3实验代码：

num=[5,25,30];

den=[1 ,6,10,8];

G=tf(num,den);

p=pole(G)

step(G,6)

代码结果：

p =

-4.0000 + 0.0000i

-1.0000 + 1.0000i

-1.0000 - 1.0000i

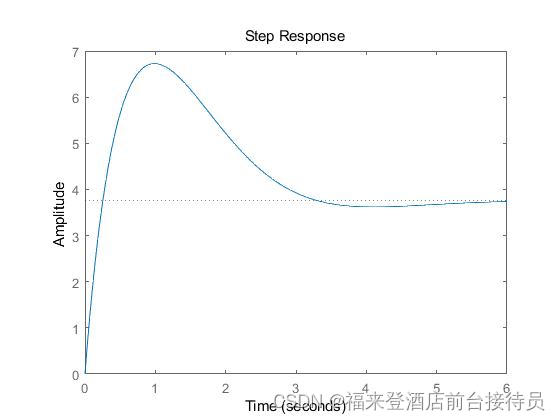
4.继续增加函数Φ(s)=20(s+0.5)(s+3)/(s+4)(s^2+2s+2)，得到结果。

4实验代码：

num=[20,70,30];

den=[1 ,6,10,8];

G=tf(num,den);

p=pole(G)

step(G,6)

代码结果：

p =

-4.0000 + 0.0000i

-1.0000 + 1.0000i

-1.0000 - 1.0000i

表4-1：高阶系统动态性能分析比较（▲=2%）

编号 Sys	上升时间 Ts/s	峰值时间 Tp/s	超调量 Mp%	调节时间 t/s
1	0.505	1.43	22.5	3.35
2	3.3	无	0	7.05
3	1.03	2.22	7.28	3.64
4	0.2	0.989	79.4	5

结论:

闭环系统极点越靠近虚轴，系统响应越慢。零点越远离虚轴，系统响应越慢。当零点靠近虚轴而极点远离虚轴时，系统响应变快。

我的其他专栏：

关注我了解更多