目录
5.1 基本概念
5.2 类别可分性测度
5.3 基于类内散布矩阵的单类模式特征提取
5.4 基于K-L变换的多类模式特征提取
5.1 基本概念
1.两种数据测量情况
① 由于测量上可实现性的限制或经济上的考虑,所获得的测量值为数不多。
② 能获得的性质测量值很多。如果全部直接作为分类特征,耗费机时,且分类效果不一定好。有人称之为“特征维数灾难”。
特征选择和提取的目的:经过选择或变换,组成识别特征,尽可能保留分类信息,在保证一定分类精度的前提下,减少特征维数,使分类器的工作即快又准确。
2.对特征的要求
(1) 具有很大的识别信息量。即应具有很好的可分性。
(2) 具有可靠性。模棱两可、似是而非、时是时非等不易判别
的特征应丢掉。
(3) 尽可能强的独立性。重复的、相关性强的特征只选一个。
(4) 数量尽量少,同时损失的信息尽量小。
3. 特征选择和特征提取的异同
1)特征选择:从L个度量值集合{x1,x2,.....xl} 中按一定准 则选出供分类用的子集,作为降维(m维,m < L)的分类 特征。
(2)特征提取:使一组度量值(x1,x2.....xl) 通过某种变换 h()产生新的m个特征(y1,y2....ym) ,作为降维的分类特征,
其中i=1,2,......,m;m<l
当模式在空间中发生移动、旋转、缩放时,特征值应保持不变,保证仍可得到同样的识别效果。
例:特征选择与特征提取的区别:对一个条形和圆进行识别。
解:[法1] ① 特征抽取:测量三个结构特征
(a) 周长 (b) 面积 (c)两个互相垂直的内径比
② 分析:(c)是具有分类能力的特征,故选(c), 扔掉(a) 、 (b) 。
—— 特征选择:一般根据物理特征或结构特征进行压缩。
[法2]:① 特征抽取:测量 物体向两个坐标轴的投影 值,则A、B各有2个值域区 间。可以看出,两个物体的 投影有重叠,直接使用投影 值无法将两者区分开。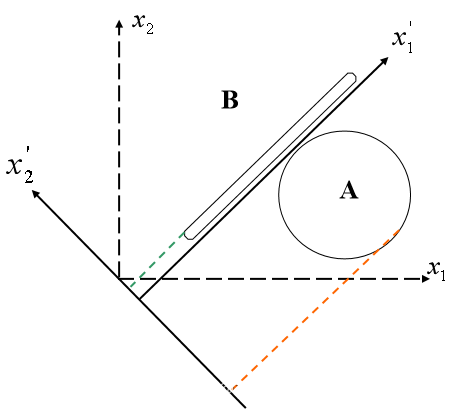
② 分析:将坐标系按逆时针方向做一旋转变化,或物体按顺时针方向变,并适当平移等。根据物体在 轴上投影的坐标值的正负可区分两个物体。
—特征提取,一般用数学的方法进行压缩。
5.2 类别可分性测度
类别可分性测度:衡量类别间可分性的尺度。
类别可分性测度:空间分布:类内距离和类间距离
随机模式向量: 类概率密度函数
错误率 :与错误率有关的距离
5.2.1 基于距离的可分性测度
1.类内距离和类内散布矩阵
1) 类内距离:同一类模式点集内,各样本间的均方距离。
式中,R:该类模式分布的自相关矩阵;
M:均值向量;
C:协方差矩阵;
2) 类内散布矩阵:表示各样本点围绕均值的散布情况
——该类分布的协方差矩阵。
特征选择和提取的结果应使类内散布矩阵的迹愈 小愈好。
2.类间距离和类间散布矩阵
1) 类间距离:模式类之间的距离,记为
2) 类间散布矩阵:表示c类模式在空间的散布情况,记为Sb。
3) 类间距离与类间散布矩阵的关系:类间散布矩阵的迹愈?愈有利于分类。
3.多类模式向量间的距离和总体散布矩阵
1)两类情况的距离:
两个类区之间的距离 = p×q个距离的平均距离
2)多类情况的距离

多类模式向量之间的平方距离=各类平方距离的先验概率加权和
多类模式向量之间的距离:模式类间的距离 模式类内的距离
3)多类情况的散布矩阵
多类类间散布矩阵 :

4)多类模式平均平方距离与总体散布矩阵的关系
![]()
距离与散布矩阵作为可分性测度的特点:
* 计算方便,概念直观(反映模式的空间分布情况 );
* 与分类错误率没有直接的联系。
5.2.2 基于概率分布的可分性测度
1.散度
1)散度的定义
出发点:对数似然比含有类别的可分性信息。
对不同的X,似然函数不同,对数似然比体现的可分性不同,通常采用平均可分性信息——对数似然比的期望值 。
散度等于两类的对数似然比期望值之和。
散度表示了区分ωi类和ωj类的总的平均信息。——特征选择和特征提取应使散度尽可能的大。
2)散度的性质

(3)错误率分析中,两类概率密度曲线交叠越少,错误率越小。
由散度的定义式
可知,散度愈大,两类概率密度函数曲线相差愈大,交叠愈少,分类错误率愈小。
(4)
3)两个正态分布模式类的散度
设ωi类和ωj 类的概率密度函数分别为
资料仅供学习使用
如有错误欢迎留言交流
上理考研周导师的其他专栏:
上理考研周导师了解更多


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










