欧拉方法
| 本条目需要扩充。(2010年2月26日) |
| 本条目没有列出任何参考或来源。(2010年2月26日) |
在数学和计算机科学中,欧拉方法,命名自它的发明者莱昂哈德·欧拉,是一种一阶数值方法,用以对给定初值的常微分方程(即初值问题)求解。它是一种解决常微分方程数值积分的最基本的一类显型方法(Explicit method)。
目录[隐藏] |
[编辑]非形式化的几何诠释
考虑计算下面一个未知曲线的形状:它具有给定的起点并且满足一个给定的微分方程。 这里,所谓“微分方程”可以看作能够通过曲线上任意点的位置而计算出这一点的切线斜率的公式。
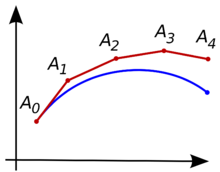
思路是,一开始只知道曲线的起点(假设为 ),曲线其他部份是未知的,不过通过微分方程,
),曲线其他部份是未知的,不过通过微分方程, 的斜率可以被计算出来,也就得到了切线。
的斜率可以被计算出来,也就得到了切线。
顺着切线向前走一小步到点 。如果我们假设
。如果我们假设 是曲线上的一点(实际上通常不是),那么同样的道理就可以确定下一条切线,依此类推。在经过几步之后,一条折线
是曲线上的一点(实际上通常不是),那么同样的道理就可以确定下一条切线,依此类推。在经过几步之后,一条折线 就被计算出来了。大部分的情况下,这条折线与原先的未知曲线偏离不远,并且任意小的误差都可以通过减少步长来得到(虽然对于刚性方程而言会比较复杂。下文将提到)。
就被计算出来了。大部分的情况下,这条折线与原先的未知曲线偏离不远,并且任意小的误差都可以通过减少步长来得到(虽然对于刚性方程而言会比较复杂。下文将提到)。
[编辑]欧拉方法的推导
以以下微分方程为例
希望用 y 在点 (t0,y(t0)) 附近的线性近似来得到其近似解(也就是 y 的泰勒展开式的前二项)。利用时间 tn时的数值,若用单步的欧拉方法,可得到时间 tn+1 = tn + h 时的近似值如下:
欧拉方法是一种显型方法,也就是说  的解是
的解是 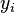 ,
,  的显函数。
的显函数。
欧拉方法可以求解一阶的微分方程,一个 阶的微分方程可以用导入
阶的微分方程可以用导入  个变量来表示
个变量来表示 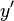 ,
,  , ...,
, ..., 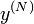 的方式,分解为
的方式,分解为 个一阶的微分方程。因此可以用欧拉方法求解以下的向量
个一阶的微分方程。因此可以用欧拉方法求解以下的向量  来得到高阶微分方程的解。
来得到高阶微分方程的解。
[编辑]应用例题
设微分方程为  ,初始值为
,初始值为 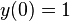 , 试用欧拉方法求
, 试用欧拉方法求  的近似值,步长为
的近似值,步长为  .
.
欧拉法则表达式:
首先求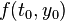 当
当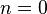 . 此微分方程仅有一个变量
. 此微分方程仅有一个变量  , 因此无须考虑给
, 因此无须考虑给 赋值.
赋值.
以上解得切线的斜率,切点 在解曲线上。回顾斜率的定义:在单位时间内,
在解曲线上。回顾斜率的定义:在单位时间内, 变量和
变量和 变量的比值, 可以计作为
变量的比值, 可以计作为 .
.
重复以上步骤求出 和
和  的值.
的值.
由于欧拉法则属于递归算法,为了避免出现计算错误,建议使用Excel或者类似的制表程序
 | 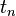 |  |  | 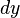 |  |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 2 |
| 2 | 1 | 2 | 1 | 2 | 4 |
| 4 | 2 | 4 | 1 | 4 | 8 |










 的数值积分。蓝色为欧拉法,绿色为
的数值积分。蓝色为欧拉法,绿色为
 步长
步长


 时的结果。可以看出中点法比欧拉法收敛更快。
时的结果。可以看出中点法比欧拉法收敛更快。

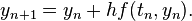




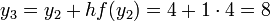














 945
945

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








