from:http://blog.csdn.net/sj13051180/article/details/6727318
1. 有一个整数数组,请求出两两之差绝对值最小的值。记住,只要得出最小值即可,不需要求出是哪两个数。(Microsoft)
方法1:两两作差求绝对值,并取最小,O( n2 )。
方法2:排序,相邻两点作差求绝对值,并取最小,O( nlgn ).
方法3:有没有O( n )的解法?网上有如下解法:
设数组A = { a1, a2, … , an }, 求 s = min( |ai - aj| ), 其中1<= i, j <=n.
设B = { b1, b2, … , bn-1 }, 且 bi = ai – ai+1
即:b1 = a1 – a2, b2 = a2 – a3, b3 = a3 – a4, …
于是有如下规律:
例如:a3 – a5 = ( a3 – a4 ) + ( a4 – a5 ) =b3 + b4
a1 – a6 = b1 + b2 + … + b5
即:ai – aj = bi + … + bj-1
则数组A中任意两个数的差,都可以用数组B中一个字段的和表示。
则原问题可以转换为:
在数组B中,求连续的某一段,使其和的绝对值最小。(只求最小值,不需要知道具体是哪些数)
例如 B = { 1, -2, 3, -1, -9, 7, -5, 6 };
则绝对值最小值为0,具体是{ -2, 3, -1 } 或 {3, -1, -9, 7}
网上的解法,一般到这里就没下文了。只是简单的提了一下,类似于最大子序列的和。具体怎么做,还要自己想想。
最大子序列和利用DP,可O( n )求解。这题咋做?纠结。
2. 写一个函数,检查字符是否是整数,如果是,返回其整数值。(或者:怎样只用4行代码编写出一个从字符串到长整形的函数?)
据说此题是,Microsoft的大牛只有了4行代码就给出了答案。
可惜,不知道是怎么写的。自己试着写写,当然可能会不至4行。单纯追求行数,也没什么意义,如果你愿意可以把所有的程序都写成一行。
注意:
1. 处理前导空格
2. 处理正负号
3. 处理进制(16进制、8进制、10进制)
4. 非法字符( 0---9, a---f, A---F)
5. 注意整数的范围,不能溢出
- bool StrToInt( char *pc, long &value )
- {
- //去掉前导空格
- while( ( *pc==' ' || *pc=='\t' ) && *pc != '\0' ) pc++;
- if( *pc == '\0' ) return false;
- //处理正负号
- int sign = 1;
- if( *pc == '+' || *pc == '-' )
- {
- if( *(pc+1) =='\0' ) return false;
- if( *pc == '-' ) sign = -1;
- pc++;
- }
- //处理数值
- long tmp = 0;
- while( *pc != '\0' )
- {
- tmp *= 10;
- //++优先级比*高
- if( *pc < '0' && *pc > '9' ) return false;
- tmp += ( *pc++ - '0' );
- }
- value = tmp * sign;
- return true;
- }
3. 给出一个函数来输出一个字符串的所有排列
方法1:
一个简单的DFS。从后往前不断交互。N个字母求全排列,O( n! )。具体实现,看代码吧。
方法2:
如果不会写递归,也可以利用STL。STL里有一个next_permutation函数。利用这个函数可以返回大于原字符串的下一个字典序列。当字符串为最大字典序列时,函数返回false。这样只要先对原字符串排序,然后不断调用next_permuation即可。
- inline void Exchange( char *px, char *py )
- {
- char tmp = *px;
- *px = *py;
- *py = tmp;
- }
- void PrintStrPermut( char *pstr, char *pbegin )
- {
- //处理空字符串
- if( pstr == NULL || pbegin == NULL ) return;
- //递归终止条件
- if( *pbegin == '\0' )
- cout << pstr << endl;
- else
- {
- for( char *p=pbegin; *p!='\0'; p++ )
- {
- Exchange( p, pbegin );
- PrintStrPermut( pstr, pbegin+1 );
- Exchange( p, pbegin );
- }
- }
- }
- void PrintStrPermut2( char *pstr )
- {
- char *p = pstr;
- while( *p != '\0' ) p++;
- sort( pstr, p );
- cout << pstr << endl;
- while( next_permutation( pstr, p ) )
- {
- cout << pstr << endl;
- }
- }
4.请编写实现malloc()内存分配函数功能一样的代码
这题比较难,要是不懂点OS的内存管理,根本就无从下手。
我们知道调用malloc()后,OS就要想方设法为我们返回一块空闲空间。这就涉及到OS的内存管理。OS的内存管理可以这样考虑:
假设整块内存有128K
初始状态,128K都是空闲
第一次请求,申请了16k,空闲112K
第二次请求,申请了32K,空闲80K
第三次请求,申请了8K,空闲72K
第二次请求申请的32K被释放,空闲108K
第四次请求,申请了24K,空闲84K
…
从上面的例子可以看出,一整块连续的空闲内存块,经过一段时间的使用,会被无情的划分为许多小块。这些小块大小不等,并且有的空闲、有的被占用。
当调用malloc时,OS就沿内存扫描,找到一块够大的空闲块,从中划分出要使用的部分,将这部分标记为己分配,并返回这部分的首地址。如果,空闲的块都是些小的碎片,那就悲具了(当然,OS可以把将相邻的空闲块合并,再尝试)。
现在,模拟一下malloc的过程:
为了便于管理,首先定义内存控制块mcb。这个mcb记录两个信息:块是否空闲、块的大小。即,每个分配出去的块,其实都带有一个mcb,只不过这个mcb位于块的最前端,返回该用户的指针刚好指向mcb之后,所以对用户是不可见的。
现在,就可以处理free了。Free只要把已分配的内存块重新标记为空闲即可,这里当然要用到该快的mcb了。
Malloc简单来说,就是维护几个指针,根据分配请求修改指针位置。对于要分配的块,将标记置位己分配,并返回这部分的首地址。
参考http://lklkdawei.blog.163.com/blog/static/32574109200881445518891/,这里讲的很清楚,还附有代码,我就不狗尾续貂了。
5. 字符串A的后几个字节和字符串B的前几个字节重叠。
这题似乎没什么玄机,就是个简单的字符串处理。使用strlen和memcpy可以完成,见代码。
- bool StrOverlap( char *strA, char *strB, int cnt, char *strC )
- {
- int sizeA = (int)strlen( strA );
- int sizeB = (int)strlen( strB );
- if( cnt > sizeA || cnt > sizeB ) return false;
- memcpy( strC, strA, sizeA-cnt );
- memcpy( strC+sizeA-cnt, strB+cnt, sizeB-cnt );
- //注意添加结束标记
- strC[sizeA+sizeB-2*cnt] = '\0';
- return true;
- }
6. 怎样编写一个程序,把一个有序整数数组放到二叉树中?
由数组建立排序二叉树。因为数组已排序,所以可以进行类似排序二叉树上的查找。感觉有点类似先序遍历,每次先处理根节点,然后分别是左子树、右子树。具体做法是:
1.整个数组对应一个二叉树,则中间元素对应二叉树的根节点
2.中间元素左边的部分对应左子树、右边的部分对应右子树
3.对左右两部分再继续递归调用。
- struct BiTreeNode
- {
- int data;
- BiTreeNode* leftChild;
- BiTreeNode* rightChild;
- //构造函数,初始化成员变量
- BiTreeNode(): data(0), leftChild(0), rightChild(0){};
- };
- void ArrayToTree( int *pi, int left, int right, BiTreeNode *&root )
- {
- if( left <= right )
- {
- int mid = ( left + right ) / 2;
- root = new BiTreeNode;
- root->data = pi[mid];
- ArrayToTree( pi, left, mid-1, root->leftChild );
- ArrayToTree( pi, mid+1, right, root->rightChild );
- }
- }
7. 怎样从顶部开始逐层打印二叉树结点数据?请编程。
用队列容易实现。网上有人说有非队列的实现,不过还是用指针把每一层的点都连了起来,然后逐层打印。这种方法和用队列把每层的节点存起来大同小异。- void PrintTreeByLevel( BiTreeNode *&root )
- {
- if( root != NULL )
- {
- queue<BiTreeNode> que;
- que.push( *root );
- while( !que.empty() )
- {
- BiTreeNode curNode = que.front();
- que.pop();
- cout << curNode.data << " ";
- if( curNode.leftChild != NULL ) que.push( *curNode.leftChild );
- if( curNode.rightChild != NULL ) que.push( *curNode.rightChild );
- }
- }
- }
8.怎样把一个链表掉个顺序(也就是反序,注意链表的边界条件并考虑空链表)?
这题主要看有没有额外存储空间的限制。
如果没有,可以重新生成一个链表,该链表是原链表的反序。具体做的时候,每次只需把新节点插入的头结点的前面即可。此时,空间复杂度O(n).
如果有存储空间的限制,要求为O(1),即只能用常数个辅助变量。这时可以用三个指针来实现。首先,需要一个指针cur,指向要反向的节点。因为链表反序,指针要指向前一个,而单链表无法直接得到前一个,所以需要一个指针pre。然后,当指针cur反向后,就无法指向下一个,所以需要一个指针next,用于保存cur的下一个。这样只要遍历整个链表,不断使指针cur所指节点反向即可。
- struct ListNode
- {
- int data;
- ListNode *next;
- ListNode(): data(0), next(0) {};
- };
- //假设没有哨兵元素
- ListNode* ReverseList( ListNode *head )
- {
- //空链表
- if( head == NULL ) return NULL;
- //只有一个元素的链表
- if( head->next == NULL ) return head;
- //至少有两个元素
- ListNode *pre, *cur, *next;
- pre = head;
- cur = pre->next;
- next = NULL;
- while( cur != NULL )
- {
- //保存下一个节点的指针
- next = cur->next;
- cur->next = pre;
- pre = cur;
- cur = next;
- }
- head->next = NULL;
- head = pre;
- return head;
- }
9.请编写能直接实现int atoi(const char * pstr)函数功能的代码。
需要注意的问题:
1.前导白空
2.正负号
3.不同进制
4.非法字符
5.Int范围
- int MyAtoi(const char * pstr)
- {
- //去除前导空格
- while( *pstr == ' ' || *pstr == '\t' ) pstr++;
- //判断正负号
- int sign = 1;
- if( *pstr == '+' || *pstr == '-' )
- {
- if( *pstr == '-' ) sign = -1;
- pstr++;
- }
- //判断进制
- int base = 10;
- if( *pstr == '0' )
- {
- pstr++;
- //以0开头的为八进制
- base = 8;
- //以0x开头的为16进制
- if( *pstr == 'X' || *pstr == 'x' )
- {
- base = 16;
- pstr++;
- }
- }
- //处理数值部分,注意非法字符
- long value = 0;
- while( *pstr != '\0' )
- {
- if( base == 10 && ( *pstr < '0' || *pstr > '9' ) ||
- base == 8 && ( *pstr < '0' || *pstr > '7' ) ||
- base == 16 && !( ( *pstr >= '0' && *pstr <= '9' ) ||
- ( *pstr >= 'A' && *pstr <= 'F' ) ||
- ( *pstr >= 'a' && *pstr <= 'f' ) )
- )
- return 0;
- value *= base;
- if( base == 16 )
- {
- if( *pstr >= '0' && *pstr <= '9' ) value += ( *pstr - '0' );
- if( *pstr >= 'a' && *pstr <= 'f' ) value += ( *pstr - 'a' ) + 10;
- if( *pstr >= 'A' && *pstr <= 'F' ) value += ( *pstr - 'A' ) + 10;
- }
- else
- {
- value += *pstr - '0';
- }
- pstr++;
- }
- //判断是否溢出
- if( value > INT_MAX || value < INT_MIN ) return 0;
- return value * sign;
- }
10.编程实现两个正整数的除法,当然不能用除法操作符。
// return x/y.
int div(const int x, const int y)
{
....
}
a/b=x, 即求a里面有多少个b.
方法一:枚举,b*1,b*2,b*3,…,直到b*x == a 或 b*x < a && b*(x+1) > a,复杂度O( a/b)这样
方法二:
除了x = 1+…+1(x个1相加),x还可以用2的幂的和表示(如4 = 2^2, 7 = 2^2+2+1 )。不用逐一枚举,类似折半查找。不断划分区间,用区间比较。
不断尝试b*(1<<0),b*(1<<1),b*(1<<2),…,
直到b*(1<<m) < a && b*(1<<m+1) > a,
则从a - b*(1<<m),然后再重新开始。
- int Div( const int x, const int y )
- {
- if( x < y ) return 0;
- int tmp = x;
- int ans = 0;
- while( tmp >= y )
- {
- int cnt = 1;
- while( ( y * cnt ) <= tmp ) cnt <<= 1;
- cnt >>= 1;
- ans += cnt;
- tmp -= y * cnt;
- }
- return ans;
- }
11.在排序数组中,找出给定数字的出现次数。比如[1, 2, 2, 2, 3] 中的出现次数是次。
方法一:直接遍历,首先找到这个数,然后逐一计数,O(n)可完成。
方法二:二分查找,首先找到这个数的第一个,记录其位置。再二分查找,找到这个数的最后一个,记录其位置。最后下边相减,O(lgn)可完成。虽然两次都是二分查找,但还是略微有点区别。
LowerSearch把相等的情况划归到左半部分,所以计算mid时要向下取整。
UpperSearch把相等的情况划归到右半部分,所以计算mid时要向上取整。
- //target出现的第一个位置
- int LowerSearch( int *pi, int left, int right, int target )
- {
- while( left < right )
- {
- //mid向下取整
- int mid = ( left + right ) / 2;
- if( target <= pi[mid] )
- {
- right = mid;
- }
- else
- {
- left = mid + 1;
- }
- }
- return left;
- }
- //target出现的第最后一个位置
- int UpperSearch( int *pi, int left, int right, int target )
- {
- while( left < right )
- {
- //这里mid向上取整
- int mid = ( left + right + 1 ) / 2;
- if( target >= pi[mid] )
- {
- left = mid;
- }
- else
- {
- right = mid - 1;
- }
- }
- return left;
- }
- int GetCount( int *pi, int left, int right, int target )
- {
- int first = LowerSearch( pi, left, right, target );
- int second = UpperSearch( pi, left, right, target );
- return second-first+1;
- }
12.平面上N个点,每两个点都确定一条直线,求出斜率最大的那条直线所通过的两个点(斜率不存在的情况不考虑)。时间效率越高越好。
按照一般的方法,逐个求斜率比较,O(n^2)可完成。有没有更快的方法?有。
对所有的点按x坐标排序,然后只比较相邻两点的斜率即可。复杂度O( nlgn )。当然,只要有了算法,编程实现很容易,关键是为什么?
我不会严格的证明,只能朴素的理解一下。
设有三个点A、B、C
如果A、B、C在一条直线上,则斜率相等
如果A、B、C不在一条直线上,则构成三角形ABC。不妨设Xa < Xb < Xc
即按照x坐标排序后,A、B相邻,B、C相邻。也就是说,三角形中AC为最长边。如图,显然Kab和Kbc中至少有个大于Kac.

13.一个整数数列,元素取值可能是~65535中的任意一个数,相同数值不会重复出现。是例外,可以反复出现。
请设计一个算法,当你从该数列中随意选取个数值,判断这个数值是否连续相邻。
注意:
- 5个数值允许是乱序的。比如:8 7 5 0 6
- 0可以通配任意数值。比如:7 5 0 6 中的可以通配成或者
- 0可以多次出现。
- 复杂度如果是O(n2)则不得分。
首先对这5个数进行排序。
如果5个数中没有0,那么用最大值 – 最小值。如果差值= 4,则连续。否则,不连续。
如果5个数中有0,则0必然排在最前面。依旧最大值 – 最小值。当差值取1,说明只有2个非0数,必然连续,则其余的数都可用0补齐。那么在连续的情况下差值最大取多少?最大值为4。这时必然有一个数不连续,但是可以用0补.
综上:
1. 先排序
2. 用非零最大值 - 非零最小值,如果差值<=4,则连续。否则,不连续。
3. 处理没有非零最大值或非零最小值的情况。
A. 全为零,必连续 B. 只用一个非0值,也连续
14.设计一个算法,找出二叉树上任意两个结点的最近共同父结点。复杂度如果是O(n2)则不得分。
经典的LCA问题,有非常成熟的解法,用tarjan算法或转换为RMQ问题。Tarjan自己没写过。这里是RMQ的解法。对于RMQ也有多种解法,比如线段树、ST等。这里讨论一下ST算法。
RMQ问题:RMQ( A, i, j )表示在数组A中求A[i]…A[j]之间最小值的下标。
首先,把LCA转换为RMQ问题。
对二叉树进行DFS,记录每个节点被访问的顺序。因为有回溯,除了根节点,每个节点都被访问2次。设二叉树有n个节点,则DFS完成后回记录2n-1个节点,然后由这些节点构成数组path,该数字记录了DFS遍历节点的顺序。
在进行DFS时,同时记录各节点的层数,组成数组level。
对二叉树上的任意两点x和y, 找到x 、y在数组path中第一次出现的位置,记为pos(x), pos(y)。则path[ pos(x) ]…path[ pos(y) ]代表在二叉树上从x遍历到y的一条路径,那么该路径上level最小的点就是x 、y的LCA。
即LCA( A, i, j ) = RMQ( level, pos(x), pos(y) )
RMQ问题的ST求解。ST,实质上属于DP。
定义:dp[i][j]表示数字A中,A[i]…A[i+2^j-1]中(即由A[i]开始的连续2^j个元素)最小值的下标
状态转换方程:dp[i][j] = Min( dp[i][j-1], dp[i+2^(j-1)][j-1] );
大概解释一下:状态方程把A[i]…A[i+2^j-1]共2^j个元素,分成两部分A[i]…A[i+2^(j-1)-1]和A[[i+2^(j-1)]…A[j],每部分2^( j-1 )个元素,然后取两部分的最小值即可。
上述部分,其实就是个DP的预处理过程。完成了预处理,最后就是RMQ问题的求解, RMQ( A, i, j ) = ?
有了上述的dp[][],只要想办法把A[i]…A[j]分成两部分,使每部分的长度为2^k。这样就可以查dp[][]数组了。对于这两部分有什么要求吗?两部分合起来刚好覆盖整个[ i, j ]区间,这当然是最好的了。但是,有时很难取到整数,所以连部分通常是交叉的,甚至每一部分几乎覆盖了整个区间。
即,2^k = j - i + 1,则可求 k=lg( j-i+1 )。k是下取整。
最终:RMQ( A, i, j ) = Min( dp[i][k], dp[j-2^k+1][j] )
RMQ的ST求解见代码
- #include <iostream>
- using namespace std;
- const int MAX = 100;
- //dp[i][j] 表示从i开始到为i+2^j -1中值最小的一个值(从i开始2^j个数)
- //dp[i][j] = min( dp[i][j-1], dp[i+2^(j-1)][j-1] );
- //查询RMQ( i, j )
- //将i,j分成两个2^k个区间
- //k = log2( j - i + 1 )
- //查询结果 min( dp[i][k], dp[j-2^k+1][k] )
- int dp[MAX][MAX];
- inline int Min( int x, int y )
- {
- return x < y ? x : y;
- }
- //使用DP,建立查询表
- void MakeRmqIndex( int *data, int size )
- {
- int i, j;
- for( i=0; i<size; i++ )
- {
- dp[i][0] = i;
- }
- for( j=1; (1<<j)<size; j++ )
- {
- for( i=0; i+(1<<j)-1 < size; i++ )
- {
- dp[i][j] = data[ dp[i][j-1] ] < data[ dp[i+(1<<(j-1))][j-1] ] ? dp[i][j-1] : dp[i+(1<<(j-1))][j-1];
- }
- }
- }
- //查表,并返回结果
- int RmqIndex( int begin, int end, int *data )
- {
- int k = (int)( log( ( end - begin + 1 ) * 1.0 )/ log( 2.0 ) );
- return data[ dp[begin][k] ] < data[ dp[end-(1<<k)+1][k] ] ? dp[begin][k] : dp[end-(1<<k)+1][k];
- }
- int main()
- {
- int data[10] = { 1, 3, 3, 4, 5, 6, 6, 7, 9, 11 };
- //返回最小索引
- MakeRmqIndex( data, 10 );
- cout << RmqIndex( 4, 9, data) << endl;
- return 0;
- }
15.一棵排序二叉树,令f=(最大值+最小值)/2,设计一个算法,找出距离f值最近、大于f值的结点。复杂度如果是O(n2)则不得分。
16. 一个整数数列,元素取值可能是1~N(N是一个较大的正整数)中的任意一个数,相同数值不会重复出现。设计一个算法,找出数列中符合条件的数对的个数,满足数对中两数的和等于N+1。复杂度最好是O(n),如果是O(n2)则不得分
这题要求O(n),我能想到就是:使用一个有N个元素的数组,然后用数值作为数组的下标,然后遍历数组。
http://blog.csdn.net/sj13051180/article/details/6727318、
from: http://blog.csdn.net/sj13051180/article/details/6733655
1.正整数序列Q中的每个元素都至少能被正整数a和b中的一个整除,现给定a和b,需要计算出Q中的前几项,
例如,当a=3,b=5,N=6时,序列为3,5,6,9,10,12
(1)、设计一个函数void generate(int a,int b,int N ,int * Q)计算Q的前几项
(2)、设计测试数据来验证函数程序在各种输入下的正确性。
感觉有点类似归并排序的Merge。有两个数组A、B。
数组A存放:3*1、3*2、3*3…
数组B存放:5*1、5*2、5*3…
有两个指针 i, j,分别指向A、B的第一个元素。取Min( A[i], B[j] ),并将较小值的指针前移,然后继续比较。
当然,编程实现的时候,完全没有必要申请两个数组,用两个变量就可以。
- #include <iostream>
- using namespace std;
- void Generate( int a,int b,int N ,int * Q )
- {
- int tmpA, tmpB;
- int i = 1;
- int j = 1;
- for( int k=0; k<N; k++ )
- {
- tmpA = a * i;
- tmpB = b * j;
- if( tmpA <= tmpB )
- {
- Q[k] = tmpA;
- i++;
- }
- else
- {
- Q[k] = tmpB;
- j++;
- }
- }
- }
- int main()
- {
- int Q[6];
- Generate( 3, 5, 6 ,Q );
- return 0;
- }
2.有一个由大小写组成的字符串,现在需要对他进行修改,将其中的所有小写字母排在大写字母的前面(大写或小写字母之间不要求保持原来次序),如有可能尽量选择时间和空间效率高的算法c语言函数原型void proc(char *str)
也可以采用你自己熟悉的语言
应该类似快排的partition。快排的partition也有两种常见的实现:从左往右扫描、从两头往中间扫描。这里使用从左往后扫描的方式。
字符串在调整的过程中可以分成两个部分:已排好的小写字母部分、待调整的剩余部分。用两个指针i和j,其中i指向待调整的剩余部分的第一个元素,用j指针遍历待调整的部分。当j指向一个小写字母时,交换i和j所指的元素。向前移动i、j,直到字符串末尾。
- #include <iostream>
- using namespace std;
- void Proc( char *str )
- {
- int i = 0;
- int j = 0;
- //移动指针i, 使其指向第一个大写字母
- while( str[i] != '\0' && str[i] >= 'a' && str[i] <= 'z' ) i++;
- if( str[i] != '\0' )
- {
- //指针j遍历未处理的部分,找到第一个小写字母
- for( j=i; str[j] != '\0'; j++ )
- {
- if( str[j] >= 'a' && str[j] <= 'z' )
- {
- char tmp = str[i];
- str[i] = str[j];
- str[j] = tmp;
- i++;
- }
- }
- }
- }
- int main()
- {
- char data[] = "SONGjianGoodBest";
- Proc( data );
- return 0;
- }
3.如何随机选取1000个关键字。
给定一个数据流,其中包含无穷尽的搜索关键字(比如,人们在谷歌搜索时不断输入的关键字)。如何才能从这个无穷尽的流中随机的选取1000个关键字?
说实话我不会做,是看网上的答案。感觉是对的,但又说不上为什么。
思路是这样的:
1.申请一个1000个元素的数组,用于保存最后选中的关键字
2.将数据流中前1000个直接放入数组中
3.对于第n个元素(n>1000), 以1000/n的概率随机替换数组中的一个元素
这个就能保证每个元素都以1000/n的概率被选中。哎,为什么?先放这吧,以后再说。
4.判断一个自然数是否是某个数的平方。说明:当然不能使用开方运算。
也就是判断一个自然数是否是完全平方数。
方法一:从1开始逐个尝试,即判断1*1,2*2,3*3…,算法复杂度O( N^0.5 )
方法二:相当于在1…N之间找一个数x,使x*x = N。这样看就是一个查找问题,所以用折半查找。算法复杂度O( logN )。
方法三:使用完全平方数的性质:每个完全平方数都可以表示成一系列奇数的和。
不妨这样简单理解一下:
设x是一个完全平方数,即 x = a^2,所以
a^2 = ( a – 1 +1 )^2 = (a-1)^2 + 2( a – 1 ) + 1
=( (a-2) + 1 )^2 + 2( a – 1 ) + 1
=(a-2)^2 + ( 2( a – 2 ) + 1 ) + (2( a – 1 ) + 1 )
即 x = 1 + 3 + 5 + … + (2( a – 1 ) + 1 )
故x可以表示为一系列奇数的和.
因此判断完全平方数的算法:x – 1 – 3 – 5…即从x中连续不断的减去一个奇数,如果结果可以为0,则x是完全平方数。否则,不是。算法复杂度O(N ),当然由于这里做的全部是减法,可能也回比较快。
5.给定能随机生成整数1到5的函数,写出能随机生成整数1到7的函数。
关键是要保证每个数字产生的概率相等。
把能随机生成整数1到5的函数记为R15。
我的想法是:把R15调用6次,然后统计这6次中,某个数字出现的次数。比如,统计1出现的次数。1的次数[0, 6],然后给次数加一,就可以随机生成1到7之间的整数。
网上的解法:首先,调用7次R15。然后,取最大值对应的下标,由这些值构成了一个新数组。然后继续调用R15,直到最后只剩下一个数字。
{ 1,2,3,4,5,6,7 }
5,3,1,5,2,4,5
{ 1, , ,4, , ,7 }
4, , ,1, , ,3
{ 1 }
6.1024! 末尾有多少个?
求末尾0个数,也就是对1024!进行因子分解,求因子中10的个数。在进一步,因子中10的个数,就相当与质因子中2*5的个数。因为质因子5的个数比2少,所以也就是求1024!中质因子5的个数。
1,2,3,…,1024中哪些数都含有质因子5?主要有以下几类:
第一类:5的倍数,1024/5 = 204个
第二类:25的倍数,1024/25 = 40个
第三类:125的倍数,1024/125 = 8个
第四类:625的倍数,1024/625 = 1个
则,总的因子5的个数:204 + 40 + 8 + 1 = 253
当然,为什么加起来就是最后的答案?这个不难,自己想想吧。
7. 有个海盗,按照等级从5到1排列,最大的海盗有权提议他们如何分享枚金币。
但其他人要对此表决,如果多数反对,那他就会被杀死。
他应该提出怎样的方案,既让自己拿到尽可能多的金币又不会被杀死?
(提示:有一个海盗能拿到98%的金币)
很有意思的一个题。嘿嘿,不会做,也还是看网上答案的。
当有5个人时,等级为5的海盗,等级最高,他来分配。分配时要考虑两个问题:利益最大、不被杀死。至于他的分配方案会不会招来杀身之祸,完全取决于其他4个人的反应。所以考虑,4个人的情况。
当有4个人时,等级为4的海盗,等级最高,他来分配。至于他的分配方案会不会招来杀身之祸,完全取决于其他3个人的反应。所以考虑,3个人的情况。
…
当有2个人时,等级为2的海盗,等级最高,他来分配。这时他就可以肆无忌惮的分配了。分配方案:100,0。即给自己100枚金币,给等级为1的海盗0枚金币。虽然对等级为1的海盗来说很不公平,但是他反对也没用,因为只有两个人,他占不了大多数。
再来考虑三个人的问题。当有3个人时,等级为3的海盗,等级最高,他来分配。他只要在前两个人中争取一个人就行。分配方案:99,0,1。这样等级为1的海盗肯定不会反对,因为比2个人的时候分的多。只有等级为2的海盗反对,但是没有用
考虑四个人的情况。分配方案:99,0,1,0。等级为4、2的海盗满意。
五个人的情况。分配方案:98,0,1,0,1。
8.给定一个集合A=[0,1,3,8](该集合中的元素都是在,之间的数字,但未必全部包含),指定任意一个正整数K,请用A中的元素组成一个大于K的最小正整数。
比如,A=[1,0] K=21 那么输出结构应该为100。
首先,计算正整数K的位数。假设k有m位。把用A中的元素组成一个大于K的最小正整数记为x。那么x就有m位或者m+1位。
根据K的最高位,在A中选数字。分两种情况:A中的数字都比k的最高位小、A中至少有一个数字等于大于k的最高位。
1.A中的数字都比k的最高位小,则x有m+1位。这时,只要用A中的数字组成一个m+1位的最小正整数即可。
2.A中至少有一个数字等于大于k的最高位。这时x的最高位就是不小于K最高位的最小数字。然后,用同样的方法继续比较下一位。
编程实现:很烦,写的都想吐血了。
- #include <iostream>
- #include <algorithm>
- using namespace std;
- //target为int值,最多是10位数
- const int MAX_INT_CNT = 20;
- int NearestInt( int target, int *data, int size )
- {
- int ans = 0;
- //计算target的位数
- int cnt = 0;
- int tmp = target;
- while( tmp > 0 )
- {
- cnt++;
- tmp /= 10;
- }
- //将target转换为字符串
- char des[MAX_INT_CNT];
- itoa( target, des , 10 );
- string strTarget( des );
- //对数组排序
- sort( data, data+size );
- int flag = 0;
- int i, j;
- for( i=0; i<cnt; i++ )
- {
- ans *= 10;
- //遍历数组,找到一个合适的元素
- for( j=0; j<size && flag==0; j++ )
- {
- if( strTarget[i] == data[j] )
- {
- ans += data[j];
- break;
- }
- if( strTarget[i] < data[j] )
- {
- ans += data[j];
- flag = 1;
- break;
- }
- }
- if( j >= size ) flag = 2;
- //flag == 2表示前面的数字都相等,只要后面的多一位就行
- if( flag == 2 )
- {
- if( i == 0 )
- {
- //找到一个非0元素
- for( j=0; j<size; j++ )
- {
- if( data[j] > 0 )break;
- }
- ans += data[j];
- }
- else
- ans += data[0];
- }
- //flag == 1表示前面的数字比较大,后面的取最小的数字即可
- if( flag == 1 ) ans += data[0];
- }
- //如果前面的数字都相等
- if( flag == 2 )
- {
- ans *= 10;
- ans += data[0];
- }
- return ans;
- }
- int main()
- {
- int data[] = { 0, 1, 3, 8 };
- cout << NearestInt( 21, data, 4 ) << endl;
- return 0;
- }
9. 用C语言实现一个revert函数,它的功能是将输入的字符串在原串上倒序后返回。
基本的字符串操作。应该没有什么问题,比起链表的反转简单多了。
- char* Revert( char *str )
- {
- if( str != NULL )
- {
- char *begin = str;
- char *end = str;
- while( *end != '\0' ) end++;
- end--;
- while( begin != end )
- {
- char tmp = *begin;
- *begin = *end;
- *end = tmp;
- begin++;
- end--;
- }
- }
- return str;
- }
10.用C语言实现函数void * memmove(void*dest, const void *src, size_t n)。memmove函数的功能是拷贝src所指的内存内容前n个字节到dest所指的地址上。
其实就是自己写一个memcpy函数。注意下面三种情况:
指针为空
两个指针间距过小( 如dest = 10010, src =10020, n = 20 )
void*的转换
- void* Memmove( void *dest, const void *src, size_t n )
- {
- char *cDest = (char*) dest;
- char *cSrc = (char*) src;
- assert( cDest != NULL && cSrc != NULL );
- assert( cDest >= cSrc + n || cSrc >= cDest + n );
- while( n-- ) *cDest++ = *cSrc++;
- return dest;
- }
11.有一根厘米的细木杆,在第3厘米、7厘米、11厘米、17厘米、23厘米这五个位置上各有一只蚂蚁。木杆很细,同时只能通过一只蚂蚁。开始时,蚂蚁的头朝左还是朝右是任意的,它们只会朝前走或调头,但不会后退。当任意两只蚂蚁碰头时,两只蚂蚁会同时调头朝反方向走。假设蚂蚁们每秒钟可以走一厘米的距离。
编写程序,求所有蚂蚁都离开木杆的最小时间和最大时间。
不知这题是想考什么。
题目的难点在于:初始状态,蚂蚁的方向任意。因为只有5个蚂蚁,每只蚂蚁的方向只有左、右两种选择,因此5只蚂蚁的初始方向有2^5 = 32种情况。
没有想到什么好的算法,只能枚举所有情况。对每种情况,模拟蚂蚁的爬杆过程:沿初始方向前进、每秒更新一次蚂蚁的位置、更新完成后进行碰撞检测。当所有蚂蚁都爬出细杆后,就可以得到所需时间。最后,在所有的初始情况下,求最小时间和最大时间。索性数据量很小,时间可以接受。
- const int LEFT = 0;
- const int RIGHT = 1;
- //记录每个蚂蚁的初始方向
- int dir[5];
- //记录每个蚂蚁的初始位置
- int pos[5];
- //记录每个蚂蚁是否爬出了细杆
- bool isFinish[5];
- void Init( int i )
- {
- //初始化蚂蚁的方向
- int tmp = i;
- int mask = 0x0001;
- for( int j=0; j<5; j++ )
- {
- dir[j] = ( tmp & mask ) ? RIGHT : LEFT;
- tmp >>= 1;
- }
- //初始化蚂蚁的位置
- pos[0] = 3;
- pos[1] = 7;
- pos[2] = 11;
- pos[3] = 17;
- pos[4] = 23;
- //初始化蚂蚁的状态标志
- memset( isFinish, false, sizeof(isFinish) );
- }
- void AntTime( int &maxTime, int &minTime )
- {
- int max = 0;
- int min = 10000000;
- //依次处理32种情况
- for( int i=0; i<32; i++ )
- {
- Init( i );
- //记录已经爬出细杆的蚂蚁个数
- int cnt = 0;
- //每秒检测一次
- int time;
- for( time=1; ; time++ )
- {
- //更新蚂蚁位置
- for( int j=0; j<5; j++ )
- {
- if( !isFinish[j] )
- {
- if( dir[j] == LEFT )
- pos[j]--;
- else
- pos[j]++;
- }
- }
- //检测蚂蚁是否已爬出细杆
- for( int m=0; m<5; m++ )
- {
- if( !isFinish[m] && ( pos[m] < 0 || pos[m] > 23 ) )
- {
- isFinish[m] = true;
- cnt++;
- }
- }
- //如果所有的蚂蚁都已经爬出细杆,则跳出
- if( cnt >= 5 ) break;
- //如果相撞,则掉头
- for( int k=0; k<5; k++ )
- {
- if( !isFinish[k] )
- {
- if( ( k == 0 && pos[k] == pos[k+1] ) || ( k == 5 && pos[k] == pos[k-1] ) ||
- ( ( k > 0 && k < 5 ) && ( pos[k] == pos[k+1] || pos[k] == pos[k-1] ) )
- )
- {
- dir[k] = ( dir == LEFT ) ? RIGHT : LEFT;
- }
- }
- }
- }
- if( time > max ) max = time;
- if( time < min ) min = time;
- }
- maxTime = max;
- minTime = min;
- }
12.请定义一个宏,比较两个数a、b的大小,不能使用大于、小于、if语句
这里有两种做法:正数的绝对值等于本身、两数相减判断符号位
- #define MAX( a, b ) ( fabs( a, b ) == ( (a) - (b) ) ? (a) : (b) )
- #define MMAX( a, b ) ( ( ( (a) - (b) ) & ( 1 << 31 ) ) ? (a) : (b) )
13.两个数相乘,小数点后位数没有限制,请写一个高精度算法
14.有A、B、C、D四个人,要在夜里过一座桥。他们通过这座桥分别需要耗时1、2、5、10分钟,只有一支手电,并且同时最多只能两个人一起过桥。请问,如何安排,能够在17分钟内这四个人都过桥?
这题想想不难,就不知道具体编程应该怎么实现,能想到的就是DFS。这里的17分钟应该就是最短时间了。先不管编程实现了,说说具体的思路吧
首先,要到对岸,每次不能只过一个人。因为这个人拿了手电,其他人都过不了。这样,每次过桥,必须两个人。两个人过去,其中一个人再拿了手电回来。那选哪两个人过去,哪个人再回来?当然是时间最小的啦。所以,5分钟的人和10分钟的人结伴过河,这样可以把5分钟的时间淹没在10分钟内,共需10钟就可以完成。在让时间最小的人拿了手电回去,那自然选1分钟的人了。也就是说,1分钟的人必须在5、10之前到达对岸。
这样,整个过程就是:1、2先到对岸(2Min),2拿了手电返回(2Min),5、10再结伴过桥(10Min),1拿手电返回(1Min),最后1、2结伴过桥(2Min),总共刚好17分钟。
15.有12个小球,外形相同,其中一个小球的质量与其他11个不同,给一个天平,问如何用3次把这个小球找出来,并且求出这个小球是比其他的轻还是重
很久以前的题了,估计大多数人都见过。类似折半查找的方法,把问题的规模以O( lgn )的速度减小。12---6---3---1。当剩3个时,问题最精妙,这时有三种状态可利用:天平左半、天平右边、不在天平两端。这提示我们,其实27个小桥也可以用这个方法。27---9----3----1,即称3次就可以完成。
其实,这里可以总结一个规律:( 3^(n-1), 3^n ]内的数都只需n次就可以完成。即,10、11、12、….、27个球都只用3次就可以。
16.在一个文件中有10G 个整数,乱序排列,要求找出中位数。内存限制为2G。只写出思路即可。
海量数据处理的问题。10G个数,中位数就是第5G、第5G+1个数。回想一下,一般情况下求中位数的做法:类似于快排的partition,找到一个数,使比它小的数的个数占到总数的一半就行。所以,可以把数值空间分段,然后统计每一段中数据的个数,这样就可以很容易的确定中位数在那一段。找个该段后,数据量已经急剧减小了,剩下的问题就好处理了。这种方法可以说是桶排序的思想,也可以说是hash的思想。下面具体分析一下:
因为要统计每一段中数据的个数,所以可以用一个unsigned int型。unsigned int一般占4个字节,可以计数到2^32-1,大约是4G。题目中有10G个数,如果有很多数落在同一个段中,unsigned int肯定不够用。所以,这里的计数用要8字节的long long。即,相当于有一个数组,数组是long long性,数组的每一个元素,代表了一个数据段内的数据个数。这个数组有多大?为了充分利用2G内存,数组大小2G/8 = 256M。即,有数组long long cnt[256M].
假设题目中的10G个数都是4字节的int。如何把这10G个整数,映射到cnt[256M]的数组中。可以使用计算机中的虚拟地址到物理地址的转换。取int的高28位作为数组下标的索引值,这样就可以完成映射。
整个算法的流程:
扫描10G个整数,对每个整数,取高28位,映射到数组的某个元素上
给数组的这个元素加1,表示找到一个属于该数据段的元素
扫描完10G个整数后,数组cnt中就记录了每段中元素的个数
从第一段开始,将元素个数累计,直到值刚好小于5G,则中位数就在该段
这时对10G个整数再扫描一遍,记录该段中每个元素的个数。直至累计到5G即可。
17..一个文件中有40亿个整数,每个整数为四个字节,内存为1GB,写出一个算法:求出这个文件里的整数里不包含的一个整数
方法一:
使用位图。4字节的int,有4G个不同的值。每个值,对应1bit,则共需4G/8 = 512M
内存。初始状态,对512M的位图清零。然后,对这40亿个整数进行统计。如果某个值出现了,那么就把这个值对应的bit置位。最后,扫描位图,找到一个没有被置位的bit即可。
方法二:
分段统计。Long long cnt[512M/8=64M]对应数值空间的64M个数据段。每个数据段包含64个不同值,用一个long long作为这个数据段内的位图,位图占64M*8=512M。
这样扫描一遍40亿个整数后,从数组中找到一个计数小于64的元素,然后查看它的位图,找出未出现的元素。
方法二平均性能应该比方法一快,但它占的内存很恐怖。其实,这两种方法都不是很实际,总共1G的内存,算法就消耗512M甚至1G,那剩下的系统程序怎么办?OS都跑不起来了吧。
18.腾讯服务器每秒有2w个QQ号同时上线,找出5min内重新登入的qq号并打印出来。
这应该是道面试题,面试官随口问了一下。主要是看思路吧。
最简单的想法:直接用STL的set。从某一时刻开始计时,每登陆一个QQ,把它放入set,如果已存则直接打印。直到5min后,就可以over了。下面来简单分析一下算法的负复杂度:
空间复制度:用str存储每个QQ号,假设QQ号有20位,理想情况下每个QQ占20Byte。则5min内的QQ:2w * 60 * 5 = 600w个,需要的存储空间600w * 20byte = 12000w byte = 120M,这样的存储应该可以忍受吧。
时间复杂度:STL的set是用二叉树(更确切的说是:红黑树)实现的,查找效率是O( lgn ),应该还是挺快的吧。
呃,有人说不让用STL。那就自己设计一个数据结构呗。该用什么数据结构呢?想了想,还是继续用树,这里用一个trie tree吧。节点内容包括QQ号、指向子节点的指针(这里有10个,认为QQ由0---9的数字组成)。登陆时间要不要?考虑这样一个问题:是否需要把所有的QQ都保存在内存中?随着时间的增加,登陆的QQ会越来越多,比较好的方法是把长时间不登陆的QQ释放掉。所以需要记录登陆时间,以便于释放长期不登陆的QQ。
- struct TrieNode
- {
- string qq;
- int lastLoginTime;
- TrieNode *next[10];
- };
我们的trie上的操作主要有两个:查找并插入、删除。也就是说,这颗树是不断动态变化的,我们需要维护它。
from: http://blog.csdn.net/sj13051180/article/details/6754228
1.判断单链表是否有环,要求空间尽量少(2011年MTK)
如何找出环的连接点在哪里?
如何知道环的长度?
很经典的题目。
1.判断是否有环。使用两个指针。一个每次前进1,另一个每次前进2,且都从链表第一个元素开始。显然,如果有环,两个指针必然会相遇。
2.环的长度。记下第一次的相遇点,这个指针再次从相遇点出发,直到第二次相遇。此时,步长为1的指针所走的步数恰好就是环的长度。
3.环的链接点。记下第一次的相遇点,使一个指针指向这个相遇点,另一个指针指向链表第一个元素。然后,两个指针同步前进,且步长都为1。当两个指针相遇时所指的点就是环的连接点。
链接点这个很不明显,下面解释一下。
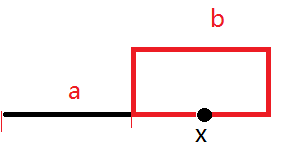
如图,设链表不在环上的结点有a个,在环上的结点有b个,前两个指针第一次在第x个结点相遇。
S( i )表示经过的总步长为i之后,所访问到的结点。
显然,环的链接点位S( a ),即从起点经过a步之后所到达的结点。
现在要证明:
从第一次的相遇点x再经过a步之后可到达链接点S( a ),即 S( x + a ) = S( a )
由环的周期性可知,只要 a = tb 其中( t = 1, 2, …. ),则S( x + a ) = S( a )
如何证明a = tb?
再看看已知条件,当两个指针第一次相遇时,必有S( x ) = S( 2x )
由环的周期性可知,必有 2x = x + bt, 即x = tb.
- struct Node
- {
- int data;
- Node* next;
- Node( int value ): data(value), next(NULL) {};
- };
- //判断单链表是否有环
- bool IsCircle( Node *pHead )
- {
- //空指针 或 只有一个元素且next为空时,必无环
- if( pHead == NULL || pHead->next == NULL ) return false;
- Node *pSlow = pHead;
- Node *pFast = pHead;
- while( ( pFast != NULL ) && ( pFast->next != NULL ) )
- {
- //分别按步长1、2前进
- pSlow = pSlow->next;
- pFast = pFast->next->next;
- if( pSlow == pFast ) break;
- }
- if( ( pFast == NULL ) || ( pFast->next == NULL ) )
- return false;
- else
- return true;
- }
- //求环的长度
- int GetLen( Node *pHead )
- {
- if( pHead == NULL || pHead->next == NULL ) return false;
- Node *pSlow = pHead;
- Node *pFast = pHead;
- //求相遇点
- while( ( pFast != NULL ) && ( pFast->next != NULL ) )
- {
- pSlow = pSlow->next;
- pFast = pFast->next->next;
- if( pSlow == pFast ) break;
- }
- //计算长度
- int cnt = 0;
- while( ( pFast != NULL ) && ( pFast->next != NULL ) )
- {
- pSlow = pSlow->next;
- pFast = pFast->next->next;
- cnt++;
- //再次相遇时,累计的步数就是环的长度
- if( pSlow == pFast ) break;
- }
- return cnt;
- }
- //求环的入口点
- Node* GetEntrance( Node* pHead )
- {
- if( pHead == NULL || pHead->next == NULL ) return false;
- Node *pSlow = pHead;
- Node *pFast = pHead;
- //求相遇点
- while( ( pFast != NULL ) && ( pFast->next != NULL ) )
- {
- pSlow = pSlow->next;
- pFast = pFast->next->next;
- if( pSlow == pFast ) break;
- }
- pSlow = pHead;
- while( pSlow != pFast )
- {
- //同步前进
- pSlow = pSlow->next;
- pFast = pFast->next;
- }
- return pSlow;
- }
2.用非递归的方式合并两个有序链表(2011年MTK)
用递归的方式合并两个有序链表
基本的链表操作,没什么好说的。
非递归:就是把一个链表上的所有结点插入到另一个链表中。
递归:??
- //两个有序链表的合并
- Node* merge( Node* pHeadA, Node* pHeadB )
- {
- //处理空指针
- if( pHeadA == NULL || pHeadB == NULL )
- {
- return ( pHeadA == NULL ) ? pHeadB : pHeadA;
- }
- //处理第一个节点
- Node *px, *py;
- if( pHeadA->data <= pHeadB->data )
- {
- px = pHeadA; py = pHeadB;
- }
- else
- {
- px = pHeadB; py = pHeadA;
- }
- Node *pResult = px;
- //将py上的节点按顺序插入到px
- Node *pre = px;
- px = px->next;
- while( py != NULL && px != NULL )
- {
- //在px上找到py应该插入的位置
- while( py != NULL && px != NULL && py->data > px->data )
- {
- py = py->next;
- px = px->next;
- pre = pre->next;
- }
- //py插入到pre和px之间
- if( py != NULL && px != NULL )
- {
- //py指针前移
- Node* tmp = py;
- py = py->next;
- //pre指针前移
- Node* tmpPre = pre;
- pre = pre->next;
- //插入
- tmp->next = px;
- tmpPre->next = tmp;
- //px指针前移
- px = px->next;
- }
- else
- break;
- }
- if( px == NULL ) pre->next = py;
- return pResult;
- }
4编程实现:把十进制数(long型)分别以二进制和十六进制形式输出,不能使用printf系列
用位操作实现。十进制数在计算机里本来就是按二进制存储的,因此通过掩码和移位操作很容易输出二进制形式。这里,要注意的一点:对最高位符号位的处理。符号位应该单独处理,否则结果会出错。十六进制的处理和二进制基本相同,只是每次处理四位。
- void LongFormat( long value )
- {
- //处理符号位
- long mask = 0x1 << ( 8 * sizeof(long) - 1 );
- if( value & mask ) cout << "1";
- else cout << "0";
- //转换为二进制
- mask = 0x1 << ( 8 * sizeof(long) - 2 );
- for( int i=1; i<8*sizeof(long); i++ )
- {
- if( value & mask ) cout << "1";
- else cout << "0";
- mask >>= 1;
- }
- cout << endl;
- //处理符号位
- cout << "0x";
- mask = 0xF << ( 8 * sizeof(long) - 4 );
- long tmp = ( value & mask ) >> ( 8 * sizeof(long) - 4 );
- if( tmp < 10 )
- cout << tmp;
- else
- cout << (char)( 'a' + ( tmp - 10 ) );
- //转换为十六进制
- mask = 0xF << ( 8 * sizeof(long) - 8 );
- for( int i=1; i<2*sizeof(long); i++ )
- {
- tmp = ( value & mask ) >> ( 8 * sizeof(long) - 4 * i - 4 );
- if( tmp < 10 )
- cout << tmp;
- else
- cout << (char)( 'a' + ( tmp - 10 ) );
- mask >>= 4;
- }
- }
5.编程实现:找出两个字符串中最大公共子字符串,如"abccade","dgcadde"的最大子串为"cad"
有人说:可用KMP。可惜KMP忘了,找时间补一下。
还有人说:用两个字符串,一个作行、一个作列,形成一个矩阵。相同的位置填1,不同的位置填0。然后找哪个斜线方向上1最多,就可以得到最大公共子字符串。空间复制度0( m*n ),感觉时间上也差不多O( m*n )

没想到什么好办法,只会用最笨的办法O( m*n )。即,对于字符串A中的每个字符,在字符串B中找以它为首的最大子串。哎,即便是这个最笨的方法,也写了好长时间,汗。
- void GetSubStr( char *strA, char *strB, char *ans )
- {
- int max = 0;
- char *pAns = NULL;
- //遍历字符串A
- for( int i=0; *(strA+i) != '\0'; i++ )
- {
- //保存strB的首地址,每次都从strB的第一个元素开始比较
- char *pb = strB;
- while( *pb != '\0' )
- {
- //保存strA的首地址
- char *pa = strA + i;
- int cnt = 0;
- char *pBegin = pb;
- //如果找到一个相等的元素
- if( *pb == *pa )
- {
- while( *pb == *pa && *pb != '\0' )
- {
- pa++;
- pb++;
- cnt++;
- }
- if( cnt > max )
- {
- max = cnt;
- pAns = pBegin;
- }
- if( *pb == '\0' ) break;
- }
- else
- pb++;
- }
- }
- //返回结果
- memcpy( ans, pAns, max );
- *(ans+max) = '\0';
- }
6.有双向循环链表结点定义为:
struct node
{
int data;
struct node *front,*next;
};
有两个双向循环链表A,B,知道其头指针为:pHeadA,pHeadB,请写一函数将两链表中data值相同的结点删除。
没什么NB算法。就是遍历对链表A,对A的每个元素,看它是否在链表B中出现。如果在B中出现,则把所有的出现全部删除,同时也在A中删除这个元素。
思路很简单,实现起来也挺麻烦。毕竟,双向循环链表也算是线性数据结构中最复杂的了。如何判断双向循环链表的最后一个元素?p->next == pHead.
删除操作:
双向循环链表只有一个节点时
双向循环链表至少有两个节点时
- struct Node
- {
- int data;
- struct Node *front,*next;
- Node( int value ): data( value ), front( NULL ), next( NULL ) { };
- void SetPointer( Node *pPre, Node *pNext ) { front = pPre; next = pNext; };
- };
- //如果成功删除返回真。否则,返回假。
- bool DeleteValue( Node *&pHead, int target )
- {
- if( pHead == NULL ) return false;
- //至少有两个元素
- bool flag = false;
- Node* ph = pHead;
- while( ph->next != pHead )
- {
- Node *pPre = ph->front;
- Node *pNext = ph->next;
- if( ph->data == target )
- {
- //如果删除的是第一个元素
- if( ph == pHead ) pHead = ph->next;
- pPre->next = pNext;
- pNext->front = pPre;
- Node *tmp = ph;
- delete tmp;
- //设置删除标记
- flag = true;
- }
- ph = pNext;
- }
- //只有一个元素或最后一个元素
- if( ph->next == pHead )
- {
- if( ph->data == target )
- {
- //如果要删除的是最后一个元素
- if( ph->front != ph )
- {
- Node *pPre = ph->front;
- Node *pNext = ph->next;
- pPre->next = pNext;
- pNext->front = pPre;
- Node *tmp = ph;
- delete tmp;
- }
- else
- {
- delete pHead;
- pHead = NULL;
- }
- flag = true;
- }
- }
- return flag;
- }
- void DeleteSame( Node *&pHeadA, Node *&pHeadB )
- {
- if( pHeadA != NULL && pHeadB != NULL )
- {
- Node *pa = pHeadA;
- while( pa->next != pHeadA )
- {
- //如果B中含有pa->data,并且已经删除
- if( DeleteValue( pHeadB, pa->data ) )
- {
- //在A中删除pa->data
- Node *tmp = pa->next;
- DeleteValue( pHeadA, pa->data );
- pa = tmp;
- }
- else
- pa = pa->next;
- }
- //只有一个元素或最后一个元素
- if( DeleteValue( pHeadB, pa->data ) )
- {
- DeleteValue( pHeadA, pa->data );
- }
- }
- }
7.设计函数int atoi(char *s)。
int i=(j=4,k=8,l=16,m=32); printf(“%d”, i); 输出是多少?
解释局部变量、全局变量和静态变量的含义。
解释堆和栈的区别。
论述含参数的宏与函数的优缺点。
1.字符串转整形,嘿嘿,前面已写过了。
2.逗号表达式的值等于最后一个逗号之后的表达式的值。对应本题,即i=(m=32)
3.局部变量:在函数内定义的变量。作用域范围:只在定义它的块内有效。
全局变量:在函数之外定义的变量。作用域范围:从定义的地方开始直到文件末尾都有效。
静态变量:static变量,属于静态存储方式。静态局部变量在函数内定义,生存期是整个源代码。但是,作用域范围只在定义它的函数内有效。静态全局变量与一般的全局变量:一般全局变量在整个源程序内有效,静态全局变量只在所在文件内有效。
4.堆:一般new出来的变量都在堆里,这里变量要由程序员自己管理,即在不用的时候要及时释放,防止内存泄露。
栈:一般局部变量、函数的参数都在栈里,他们是由编译器来自动管理的。
8.顺时针打印矩阵
题目:输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
例如:如果输入如下矩阵:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
则依次打印出数字, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10。
分析:包括Autodesk、EMC在内的多家公司在面试或者笔试里采用过这道题
本来想写递归的,结果递归的终止条件比较复杂。因为每次把最外面一圈都出来了,所以矩形的行列都减小2,而且还要记录当前矩形的起始位置。递归终止条件,要考虑行列为0、1的情况。哎,想不清楚。最后还是非递归的好写。也很简单,没啥所的,直接看代码把。
- const int MAX_ROW = 100;
- const int MAX_COL = 100;
- void PrintMatrix( int data[][MAX_COL], int row, int col )
- {
- int top = 0;
- int bottom = row-1;
- int left = 0;
- int right = col-1;
- int cnt = 0;
- int total = row * col;
- while( cnt < total )
- {
- //从左到右,打印最上面一行
- int j;
- for( j=left; j<=right && cnt<total; j++ )
- {
- cout << data[top][j] <<" ";
- cnt++;
- }
- top++;
- //从上到下,打印最右面一列
- for( j=top; j<=bottom && cnt<total; j++ )
- {
- cout << data[j][right] << " ";
- cnt++;
- }
- right--;
- //从右到左,打印最下面一行
- for( j=right; j>=left && cnt<total; j-- )
- {
- cout << data[bottom][j] << " ";
- cnt++;
- }
- bottom--;
- //从下到上,打印最左边一列
- for( j=bottom; j>=top && cnt<total; j-- )
- {
- cout << data[j][left] << " ";
- cnt++;
- }
- left++;
- }
- }
9.对称子字符串的最大长度
题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出。
分析:可能很多人都写过判断一个字符串是不是对称的函数,这个题目可以看成是该函数的加强版
10.用1、2、3、4、5、6这六个数字,写一个main函数,打印出所有不同的排列,如:512234、412345等,要求:"4"不能在第三位,"3"与"5"不能相连.
先不考虑限制条件,我们可以用递归打印出所有的排列(嘿嘿,这个前面写过,可以用递归处理)。然后,只要在递归终止时,把限制条件加上,这样只把满足条件的排列打印出来,就可以了。
- bool IsValid( char *str )
- {
- for( int i=1; *(str+i) != '\0'; i++ )
- {
- if( i == 2 && *(str+i) == '4' ) return false;
- if( *(str+i) == '3' && *(str+i-1) == '5' || *(str+i) == '5' && *(str+i-1) == '3' )
- return false;
- }
- return true;
- }
- void PrintStr( char *str, char *start )
- {
- if( str == NULL ) return;
- if( *start == '\0' )
- {
- if( IsValid( str ) ) cout << str << endl;
- }
- for( char *ptmp = start; *ptmp != '\0'; ptmp++ )
- {
- char tmp = *start;
- *start = *ptmp;
- *ptmp = tmp;
- PrintStr( str, start+1 );
- tmp = *start;
- *start = *ptmp;
- *ptmp = tmp;
- }
- }
11。微软面试题
一个有序数列,序列中的每一个值都能够被2或者3或者5所整除,1是这个序列的第一个元素。求第1500个值是多少?
2、3、5的最小公倍数是30。[ 1, 30]内符合条件的数有22个。如果能看出[ 31, 60]内也有22个符合条件的数,那问题就容易解决了。也就是说,这些数具有周期性,且周期为30.
第1500个数是:1500/22=68 1500%68=4。也就是说:第1500个数相当于经过了68个周期,然后再取下一个周期内的第4个数。一个周期内的前4个数:2,3,4,5。
故,结果为68*30=2040+5=2045
12.从尾到头输出链表
题目:输入一个链表的头结点,从尾到头反过来输出每个结点的值。链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道很有意思的面试题。该题以及它的变体经常出现在各大公司的面试、笔试题中。
链表的反向输出。前面我们讨论过:链表的逆序,使用3个额外指针,遍历一遍链表即可完成。这里当然可以先把链表逆序,然后再输出。链表上使用递归一般也很简单,虽然递归要压栈,但程序看起来很简洁。
- struct ListNode
- {
- int m_nKey;
- ListNode* m_pNext;
- };
- void PrintReverse( ListNode* pHead )
- {
- ListNode* ph = pHead;
- if( ph != NULL )
- {
- PrintReverse( ph->m_pNext );
- cout << ph->m_nKey << " ";
- }
- }
from: http://blog.csdn.net/sj13051180/article/details/6765603
1金币概率问题(威盛笔试题)
题目:个房间里放着随机数量的金币。每个房间只能进入一次,并只能在一个房间中拿金币。一个人采取如下策略:前四个房间只看不拿。随后的房间只要看到比前四个房间都多的金币数,就拿。否则就拿最后一个房间的金币。编程计算这种策略拿到最多金币的概率。
这题真要用数学的方法计算,估计还真不好算。还好,题目要求用编程实现。这样它就成了一个模拟题,即用程序来模拟整个取金币的过程。
我们可以进行很多次实验(如10000次)。每次实验,对每个房间产生随机数量的金币数,然后按照题目中的策略拿金币。如果拿到的金币数恰好是最多的则成功。最后统计很多次实验中成功的次数,并计算概率。
- #include <iostream>
- #include <ctime>
- using namespace std;
- const int MAX_COIN = 100;
- const int MIN_COIN = 1;
- //初始化随机数种子
- void InitRandom()
- {
- srand( time( NULL ) );
- }
- //为每个房间产生随机数量的金币
- int GegenrateGoldCoin( int *goldCoin, int size )
- {
- int max = 0;
- for( int i=0; i<size; i++ )
- {
- goldCoin[i] = ( rand()%( MAX_COIN - MIN_COIN + 1) ) + MIN_COIN;
- if( goldCoin[i] > max ) max = goldCoin[i];
- }
- //范围最多的金币数
- return max;
- }
- //按照给定的策略从房间中拿金币
- int TakeCoin( int *goldCoin, int size )
- {
- int firstFour[4];
- int maxInFirstFour = 0;
- for( int i=0; i<4; i++ )
- {
- firstFour[i] = goldCoin[i];
- if( goldCoin[i] > maxInFirstFour ) maxInFirstFour = goldCoin[i];
- }
- for( int i=4; i<size; i++ )
- {
- //如果比前四个房间的金币都多,则拿
- if( goldCoin[i] > maxInFirstFour ) return goldCoin[i];
- }
- //拿最后一个房间的金币
- return goldCoin[size-1];
- }
- int main()
- {
- int goldCoin[10];
- int tryCnt = 10000;
- int successCnt = 0;
- InitRandom();
- //总共进行tryCnt次实验
- for( int i=0; i<tryCnt; i++ )
- {
- int max = GegenrateGoldCoin( goldCoin, 10 );
- int choose = TakeCoin( goldCoin, 10 );
- if( max == choose ) successCnt++;
- }
- cout << successCnt * 1.0 / tryCnt << endl;
- return 0;
- }
2.找出数组中唯一的重复元素
1-1000放在含有个元素的数组中,只有唯一的一个元素值重复,其它均只出现一次.每个数组元素只能访问一次,设计一个算法,将它找出来;不用辅助存储空间,能否设计一个算法实现?
设数组为A[1001] = { a1, a2, …, a1001 },重复的元素为x, 且 1 <= x <=1000。
SumA = 1+…+1000
SumB = a1 + … + a1001
所以,唯一重复的元素为:x = SumB – SumA
要注意的问题:
1. 唯一重复的元素。这点很重要,如果有不止一个重复的元素,要找出其中任意一个,就不会这么简单了。
2. 注意溢出的情况。和的范围:(1+1000)*1000/2 ≈ 1000^2 ≈ 2^20。具体编程实现的时候,使用4字节的int完全可以搞定。如果数据范围很大,比如数组中存放的元素[1, 2^40],此时和的范围(1+2^40)*2^40/2 ≈ 2^80,远远超过了8字节的long long的表示范围,求和时显然会溢出。
3.百度校园招聘的一道笔试题
题目大意如下:
一排N个正整数,其中最大值1M,且+1递增,乱序排列。第一个不是最小的,把它换成-1,最小数为a且未知,求第一个被-1替换掉的数原来的值,并分析算法复杂度。
同上一题基本相同。
设这一排数是A1、A2、A3、…、AN,这N个数分别是: a, a+1, a+2, …, a+n
被替换掉的数为X。
SumA = A1+A2+A3+…+AN
SumB =a+(a+1)+…+(a+n)
则 X + 1 = SumB – SumA
处理溢出情况:
和的最大范围a + … + 2^20 ≈ 1+…+ 2^20 ≈ (1+2^20)* 2^20/2 =2^40。使用4字节的int会溢出。
下面有种方法,可以进行一个简单的处理,但处理能力有限。
使用辅助数组data,数组的元素是Ai-(a+i-1)。则data的所有元素之和恰好是SumB – SumA。现在要说明的是:对data的所有元素求和不会溢出。
最好情况下,这一排数{A1、A2、A3、…、AN}的顺序基本和{ a, a+1, a+2, …, a+n }相同,这样除了第一个元素,其余元素对应相减都为0,因此不会溢出。
最坏情况下,{A1、A2、A3、…、AN}递减排列,{ a, a+1, a+2, …, a+n }递增排列。此时,data的前N/2个元素为正,后N/2个元素为负。相加求和时,只要前N/2个元素的和不溢出,则结果不溢出。这时,前N/2个元素分别为:
(a+n)-(a), (a+n-1)-(a+1), (a+n-2)-(a+2),…2, 0
则,前N/2个元素的和:(((a+n)-(a))*n/2)/2 = n^2/4≈(2^20)^2/4≈ 2^40
3.一道SPSS笔试题求解
题目:输入四个点的坐标,求证四个点是不是一个矩形
关键点:
1.相邻两边斜率之积等于-1,
2.矩形边与坐标系平行的情况下,斜率无穷大不能用积判断。
3.输入四点可能不按顺序,需要对四点排序。
算法步骤:
1.首先,对这四个点按照x坐标从小到大排序,设这四个点分别为A、B、C、D。
2. 如果A.x == B.x,即如果是矩形,则与坐标轴平行。
即要求C.x == D.x&&( ( A.y == C.y && B.y == D.y ) || ( A.y == D.y && B.y== C.y ) )
3. 如果A.x != B.x,则计算四条边的斜率Kab、Kac、Kdb、Kdc。如果是矩形,则有三个内角都为90度。
即要求 Kab*Kac== -1 && Kdb*Kdc == -1 && Kac*Kdc == -1.
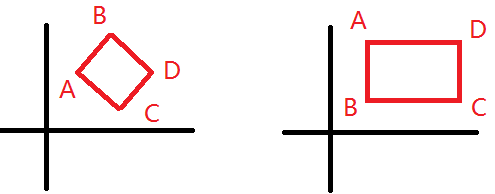
4.求两个或N个数的最大公约数和最小公倍数。
求两个数的最大公约数,即gcd( a, b ) = ?。先不管最大公约数怎么求,一旦已知最大公约数,就可以很容易得到最小公倍数。两个数的最小公倍数 = a * b / gcd( a, b)
最大公约数可以采用经典的辗转相差法。设这两个数分别是a和b, 且a > b.要证明辗转相差法,即要证明 gcd( a, b ) = gcd( b, r ),其中r = a mod b
设 c = gcd( a, b ),即 a = mc, b = nc.
且r = a – tb = mc – tnc = ( m – tn ) c
因此,gcd( b, r ) = gcd( nc, ( m – tn ) c ) = gcd( n, ( m – tn ) ) * c
即,现在要证明gcd( n, ( m – tn ) ) * c = c
即,要证明n, ( m – tn )互为质数。
再用反证法。即n, ( m – tn )存在公约数d,且d != 1
设n = xd,m – tn =yd,则m = yd + tn = yd + txd = (y+tx)d
即n = xd,m = (y+tx)d, 故gcd( a, b ) = gcd( mc,nc ) = cd != c,故矛盾
所以n, ( m – tn )互为质数
即gcd( a, b ) = gcd( b, r )
- //求a、b的最大公约数
- int GetGCD( int a, int b )
- {
- if( a < b )
- {
- //交换a、b值
- a = a + b;
- b = a - b;
- a = a - b;
- }
- //辗转相除
- while( b > 0 )
- {
- int r = a % b;
- a = b;
- b = r;
- }
- return a;
- }
还有一个问题:如何求3个数的最大公约数、最小公倍数?
5.字符串原地压缩
题目描述:“eeeeeaaaff" 压缩为 "e5a3f2",请编程实现。
多媒体压缩里的行程编码。当大量字符连续重复出现时,压缩效果惊人。编程实现比较简单,统计重复的字符个数,然后把个数转化为字符串接在原字符之后。具体编程,见代码:用两个计数指针i, j扫描字符串。i始终指向字符的第一次出现,j指向字符的最后一次出现+1。至于int转string,这里使用stringstream
- //字符串的原地压缩,即行程编码、游程编码
- void StrCompress( char *original, char *cmpr )
- {
- if( original == NULL )
- {
- cmpr = NULL;
- return;
- }
- int cnt = 0;
- int i,j;
- for( i=0, j=0; *(original+j) != '\0'; )
- {
- //统计相同字符的个数
- while( *( original + i ) == *( original + j ) )
- {
- cnt++;
- j++;
- }
- //复制字符
- *cmpr++ = *( original + i );
- //复制字符个数
- stringstream ss;
- ss << cnt;
- string strCnt;
- ss >> strCnt;
- const char *pcstr = strCnt.c_str();
- while( *pcstr != '\0' ) *cmpr++ = *pcstr++;
- cnt = 0;
- i = j;
- }
- *cmpr++ = '\0';
- }
6.字符串匹配实现
请以两种方法,回溯与不回溯算法实现。
回溯法,即最基本的方法。算法复杂度O( m * n )
设主串mainStr = { S0, S1, S2, …, Sm },
模式串matchStr = { T0, T1, T2, …, Tn };
当T[0]…T[j-1] == S[i-j]…S[i-1],即模式串的前j个字符已经和主串匹配,当前要比较T[j]和S[i]是否相等?
如果T[j] == S[i], 则i++, j++,继续比较下一个
如果T[j] != S[i], 则i要回溯,也就是i要退回到与j开始匹配时的下一个位置。同时j=0, 表示模式串从头开始,重新匹配。
不回溯:即用KMP算法。算法复杂度O( m + n )。
在KMP中,如果T[j] != S[i],则i保持不动(即,不回溯)。同时,j不用清零,而是向右滑动模式串,用T[k]和S[i]继续匹配。
算法的关键在于:模式串向右滑动多少?即K=?显然,k的值应该尽可能的大,即尽可能的向右滑动。
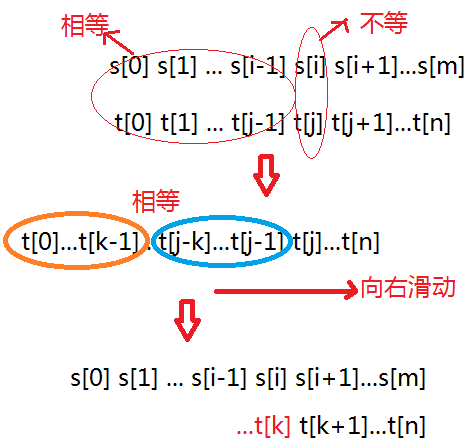
如图,如果模式串T[0]...T[j-1]前后两部分对称,也就是T[0]…T[k-1] == T[j-k]…T[j-1],则模式串可以向右滑动k个距离,即用T[k]和S[i]继续匹配。
因此 K = Max{ x | 0<=x<=j, 且T[0]…T[x-1] == T[j-x]…T[j-1]}
由上面的分析可以对于任意的j,都对应一个k,于是我们把所有的K放到一个next数组中。数组元素next[j]=k,表示当T[j]匹配失败时,下一次应该用T[k]继续匹配。现在要解决的问题就是:如何求next数组的值?当然,通过上面的理解,可以直接写出简单的字符串的next,这里我们的目标是给出一个求next的通用的方法。
求next可以用一个递归的过程。已知next[j] = k, 求next[j+1] = ?
如果T[j] == T[k],则next[j+1] = k+1
如果T[j] != T[k],则next[j+1] = ?。
这时就相当于用T[k]去匹配T[j],且匹配失败。那么,我们就应该在T[0]…T[k-1]中找到一个合适的位置x,使得T[0]…T[x-1] == T[k-x]…T[k-1]。也就是说,当用T[k]去匹配T[j]失败时,我们应该用T[x]去匹配T[j]。因此x = next[k]。整个过程相当于用模式串去匹配自身。
- #include <iostream>
- #include <cassert>
- using namespace std;
- //求next数组
- //next[j] = k:表示当matchStr[j]失配时,下一次应该用matchStr[k-1]来匹配
- void GetNext( char *str, int *next )
- {
- if( str == NULL ) return;
- for( int i=0; *(str+i) != '\0'; i++ )
- {
- if( i == 0 ) next[i] = 0;
- else if( i == 1 ) next[i] = 1;
- else
- {
- int tmp = next[i-1];
- if( str[i-1] == str[tmp-1] ) next[i] = tmp+1;
- else
- {
- //如果str[0]...str[j]前后两端有对称,找出对称位置
- while( tmp > 1 )
- {
- if( str[i-1] != str[tmp-1] ) tmp = next[tmp];
- else next[i] = tmp+1;
- }
- //如果str[0]...str[j]前后两端无对称,则next置1
- if( tmp <= 1 ) next[i] = 1;
- }
- }
- }
- }
- //字符串匹配:KMP算法,即在mainStr中找到从beginPos开始的第一个匹配位置
- int Kmp( char *mainStr, char *matchStr, int beginPos, int *next )
- {
- assert( mainStr != NULL && matchStr != NULL && beginPos >= 0 );
- int i, j;
- for( i=beginPos, j=0; *(mainStr+i) != '\0' && *(matchStr+j) != '\0'; )
- {
- //如果mainStr[i] == matchStr[j], 继续匹配下一个
- if( *(mainStr+i) == *(matchStr+j) )
- {
- i++; j++;
- }
- //如果mainStr[i] != matchStr[j],查询next数组,
- //用matchStr[next[j]-1]与mainStr[i]匹配
- else j = next[j]-1;
- }
- if( *(matchStr+j) == '\0' ) return i-j;
- else return -1;
- }
- //字符串匹配的一般算法,要回溯
- int StrMatch( char *mainStr, char *matchStr, int beginPos )
- {
- int i, j;
- for( i = beginPos; *(mainStr+i) != '\0'; i++ )
- {
- int tmp = i;
- for( j=0; *(matchStr+j) != '\0'; )
- {
- if( *(mainStr+tmp) == *(matchStr+j) )
- {
- tmp++; j++;
- }
- else break;
- }
- if( *(matchStr+j) == '\0' ) return tmp-j;
- }
- return -1;
- }
- int main()
- {
- int next[100];
- memset( next, 0, sizeof(next) );
- char *mainStr = "ababcabcacbab";
- char *matchStr = "abcac";
- GetNext( matchStr, next );
- cout << Kmp( mainStr, matchStr, 0, next ) << endl;
- cout << StrMatch( mainStr, matchStr, 0 ) << endl;
- return 0;
- }
7.取值为[1,n-1] 含n 个元素的整数数组至少存在一个重复数,O(n) 时间内找出其中任意一个重复数。
可以使用类似单链表求环的方法解决这个问题。把数组想想成一个链表,这里用数组元素的值作为下一个元素在数组中的索引。
设数组A共有n个元素,即A={ a0, a1, a2, …, an-1 }。
首先给出下标n-1,则第一个元素为A[n-1],然后用A[n-1]-1作为下标,可以到达元素A[A[n-1]-1],再以A[A[n-1]-1]为下标,可以得到元素A[A[A[n-1]-1]]…可以看到这里并没用直接用元素值作索引,而是用元素值减1,这样做是为了避免陷入死循环。
如果A[i]=A[j]=x,即x在数组中出现了两次。则A[i]--->A[x]--->…---> A[j]---> A[x],因此链表边形成了环。
一旦链表产生后,问题就简单多了。因为重复出现得到元素恰好是环的入口点。于是,问题就相当于单链表求环的入口点。用指针追过的办法,指针x每次步长为2,指针y每次步长为1。直到x、y相遇,然后重置x,使x重新开始。这次同步移动x、y,每次步长都为1,当x、y再次相遇时,恰好是环的入口点。
- //在O(n)的时间内,找出任意重复的一个数
- int FindRepeat( int *data, int size )
- {
- int x = size;
- int y = size;
- //找到相遇点
- do{
- x = data[data[x-1]-1];
- y = data[y-1];
- }while( x != y );
- //找到重复的元素
- x = size;
- do{
- x = data[x-1];
- y = data[y-1];
- }while( x != y );
- return x;
- }
























 2657
2657

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








