GitHub项目地址:地址
一、实验目的:
(1)掌握分治法思想。
(2)学会最近点对问题求解方法。
二、内容:
- 对于平面上给定的N个点,给出所有点对的最短距离,即,输入是平面上的N个点,输出是N点中具有最短距离的两点。
- 要求随机生成N个点的平面坐标,应用蛮力法编程计算出所有点对的最短距离。
- 要求随机生成N个点的平面坐标,应用分治法编程计算出所有点对的最短距离。
- 分别对N=100000—1000000,统计算法运行时间,比较理论效率与实测效率的差异,同时对蛮力法和分治法的算法效率进行分析和比较。
- 如果能将算法执行过程利用图形界面输出,可获加分。
三、算法思想提示
-
预处理:根据输入点集S中的x轴和y轴坐标进行排序,得到X和Y,很显然此时X和Y中的点就是S中的点。
-
点数较少时的情形

-
点数 ∣ S ∣ > 3 |S|>3 ∣S∣>3时,将平面点集S分割成为大小大致相等的两个子集 S L S_L SL和 S R S_R SR,选取一个垂直线L作为分割直线,如何以最快的方法尽可能均匀平分?注意这个操作如果达到效率,将导致整个算法效率达到 θ ( n 2 ) \theta(n^2) θ(n2)。
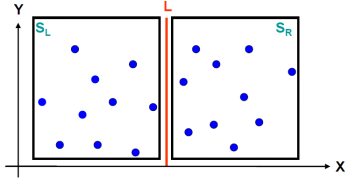
-
两个递归调用,分别求出 S L S_L SL和 S R S_R SR中的最短距离为 d l d_l dl和 d r d_r dr。
-
取 d = m i n ( d l , d r ) d=min(dl, dr) d=min(dl,dr),在直线L两边分别扩展d,得到边界区域Y,Y’是区域Y中的点按照y坐标值排序后得到的点集(为什么要排序?),Y’又可分为左右两个集合 Y ’ L Y’L Y’L和 Y ’ R Y’R Y’R
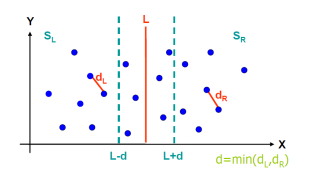
-
对于 Y ’ L Y’L Y’L中的每一点,检查Y’R中的点与它的距离,更新所获得的最近距离,注意这个步骤的算法效率,请务必做到线性效率,并在实验报告中详细解释为什么能做到线性效率?
四、实验过程及结果
一:实验结果正确性展示
随机生成了10组50个点,通过蛮力法与分治法分别求解,验证程序正确性,结果如下。
蛮力法:
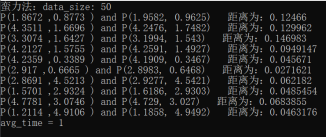
分治法:
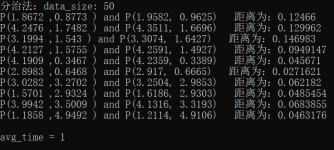
小规模测试中二者测试结果一致,答案正确。
二:蛮力法求解
-
算法原理:
(1) 存在N个点,那么就存在N(N - 1)/ 2 对点间的距离。穷举所有情况,选出最小值。 -
伪代码:
for i = 1 to N - 1
for j = i + 1 to N
if ( dis(p[i], p[j]) < min )
min = dis(p[i], p[j])
- 复杂度分析:
(1) 需要遍历 N ( N − 1 ) / 2 N(N - 1) / 2 N(N−1)/2种情况来找出最小值,最好最坏和平均情况的时间复杂度都为 O ( n 2 ) O(n^2) O(n2)
(2) 需要一个临时变量用来存储最小值,所以空间复杂度为 O ( 1 ) O(1) O(1)。 - 数据测试
使用随机数生成,均匀分布的生成了1000~35000的数据集。为了减少数据的偶然性,每个数据量都进行了10次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为20000)。理论值计算方法如下:
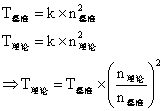
最终结果如下:


图像上符合 O ( n 2 ) O(n^2) O(n2) 二次曲线,并且理论值与实际值误差较小。
三:分治法求解
1. 分治法基本思路
本题思路:
分 – 将整体分为左右两个区域;
治 – 递归计算左右两区域的最短距离;
合 – 合并左右区域,并求合并后的最短距离;
对于本题而言,可以转化为:

(1) 分 – 将整体分为左右两个区域;
将所有点根据x坐标进行排序,取中间点。所以算法时间复杂度下限:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
m
i
d
=
(
l
+
r
)
/
2
mid = (l + r) / 2
mid=(l+r)/2
做到左右区域点集数目基本相同,降低数据随机性带来的影响
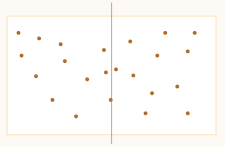
(2) 治 – 递归计算左右两区域的最短距离
子问题最小规模
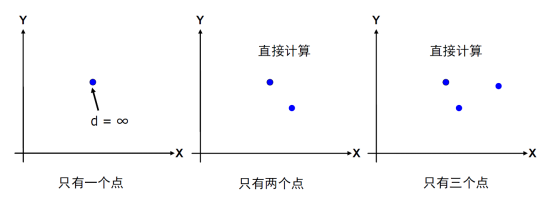
递归调用函数,即可获取左右两区域的最短距离
(3) 合 – 合并左右区域,并求合并后的最短距离

问题转化为:已知左右区域各自最短距离,求合并后的最短距离。
合并之后最短点对的选择一共有三种情况 :左+右、左+左、右+右
对于左+左、右+右的情况,利用第二步中的递归调用即可获取。
所以主要问题在于,如果最短点对来自于左+右的合并操作。
解决思路:
两点必定来自于中轴线左右两侧附近,并且两点距离小于
m
i
n
(
d
1
,
d
2
)
min(d1,d2)
min(d1,d2)
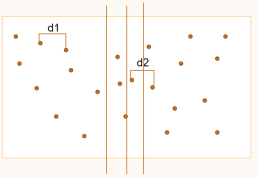

如左图所示,可以在中轴线附近取带状区域,其左右宽度为min(d1,d2)。在如此带状区域内,左右两点距离必定小于min(d1,d2),极限状态为一侧宽度长度。
问题转化为:从左右区域内各取一点,与d1,d2比较,取最短距离。
解决方法有如下展示三种。
2.分治 —— 部分蛮力
(1) 算法原理:

遍历左右带中的所有点,比较获得最短距离。
(2) 伪代码:
ans = min(d1,d2)
for i = 1 to left.size
for j = 1 to right.size
if ( dis(left[i], right[j]) < ans )
ans = dis(left[i], right[j])
(3) 复杂度分析:
对于均匀分布的大型点集,预计位于该带中的点的个数是非常少的。事实上,容易论证平均只有 O ( √ n ) O(√n) O(√n)个点是在这个带中的。
-----《数据结构与算法分析-C语言描述》P280
查询资料可知,对于均匀分布的点集而言,带中的元素个数为
√
n
√n
√n
递推公式为:
平均情况
T
(
n
)
=
2
T
(
n
/
2
)
+
(
√
n
)
2
T(n) = 2T(n/2) + (√n)^2
T(n)=2T(n/2)+(√n)2
总体时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
对于非均匀分布的点集,最差情况带中的元素个数为n
递推公式为:
最坏情况
T
(
n
)
=
2
T
(
n
/
2
)
+
(
n
)
2
T(n) = 2T(n/2) + (n)^2
T(n)=2T(n/2)+(n)2
总体时间复杂度
O
(
n
2
)
O(n^2)
O(n2)
(4) 数据分析:
最终结果如下:


图像上符合
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn) 曲线,并且理论值与实际值误差较小。
显然对于最差情况仍然为 O ( n 2 ) O(n^2) O(n2),需要改进。
3.分治 —— 多趟查询
(1) 算法原理:
遍历左带内的所有点,并与右带内所有符合条件的点进行长度比较。
右侧符合条件点集筛选过程及原理:
结论:右侧点位于以左侧点为中心,上下高度d,右侧宽度d的d*2d的范围内。且右侧点的个数存在上限。
证明如下:
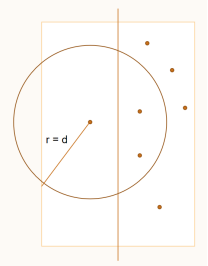
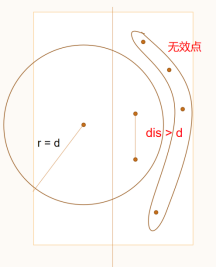
对于左侧的点,只有两点距离小于d才有合并时减小d的可能,所以右侧点必定在以左侧点为圆心、d为半径的圆内(上左图所示),其余点为无效点(上右图所示)。
又因为右侧区域内任意两点距离最小值为
d
2
≥
d
d2 \geq d
d2≥d, 所以圆内两点距离大于等于半径。

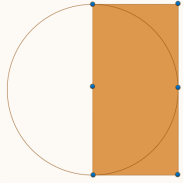
因为右侧点一定位于圆心右侧,最大可覆盖区域为右半圆,又因为两点距离大于半径,所以最多可能存在5个点满足条件(上左图所示)。
在计算机中对点坐标的排序为x或y坐标排序,难以对圆形区域进行判断,所以将半圆扩展为矩形便于计算机运算。改矩形范围内最多可能存在6个点满足条件(上左图所示)。

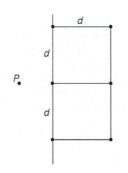
将矩形分为6个等大的2/3d*1/2d的小矩形,假设存在7个点,则必定有一个矩形内有两个点。
同一小矩形内两大距离最大值为对角线,即0.8333d < d 与题意不符,所以不能有7个点。而6个点的情况如上右图所示。
综上所述,右侧点位于以左侧点为中心,上下高度d,右侧宽度d的d*2d的范围内。且右侧点的个数存在上限。
所以在查找过程中,只需要找到第一个属于左侧点对应矩形范围内的点,并之多向上查找6次,即可完成查询。
依次遍历左带中的点,并自下而上的遍历右带直到遇到第一个符合条件的点。
(2) 伪代码:
for i = 1 to left.size
for j = 1 to right.size
if right[j] 在相应的矩形内
for k = j to j + 6 and k < right.size
ans = min(ans, dis(left[i], right[j]))
(3) 复杂度分析:
对于均匀分布的大型点集,预计位于该带中的点的个数是非常少的。事实上,容易论证平均只有O(√n)个点是在这个带中的。
-----《数据结构与算法分析-C语言描述》P280
递推公式
平均情况
T
(
n
)
=
2
T
(
n
/
2
)
+
(
√
n
)
2
T(n) = 2T(n/2) + (√n)^2
T(n)=2T(n/2)+(√n)2
总体时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
最坏情况
T
(
n
)
=
2
T
(
n
/
2
)
+
(
n
)
2
T(n) = 2T(n/2) + (n)^2
T(n)=2T(n/2)+(n)2
总体时间复杂度
O
(
n
2
)
O(n^2)
O(n2)
(4) 数据分析:
最终结果如下:


图像上符合
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn) 曲线,并且理论值与实际值误差较小。
显然对于最差情况仍然为 O ( n 2 ) O(n^2) O(n2),需要改进。
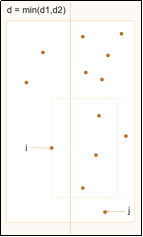
4.分治 —— 一趟查询
(1)算法原理:
此算法在上一部分的基础上进行了部分改进,达到了线性的查找效率。
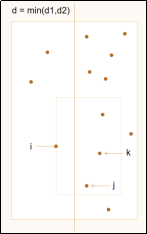
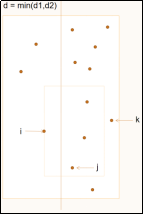
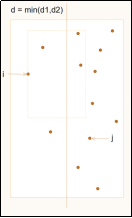
方法是对于左右侧的点都自下而上进行查找。因为矩形区域是固定的,所以随着左侧点的y坐标增大,矩形的最低点也是逐渐增大,右侧符合条件的第一个点的y也会逐渐增大,并不需要返回重新查找。(可以结合伪代码查看动图中指针的变化过程。具体过程在演示中展示。)


(2) 伪代码:
j = 0
for i = 1 to left.size
while j < right.size and right[j].y < left[i].y - d
j += 1
for k = j to j + 6 and right[k].y < left[i].y + d
ans = min(ans, dis(left[i], right[j]))
(3) 复杂度分析:
在此过程中,只需要对左右带中的点进行依次遍历,即可找到最短距离,最多比较6n次即可,达到了线性效率。
递推公式
T
(
n
)
=
2
T
(
n
/
2
)
+
n
T(n) = 2T(n/2) + n
T(n)=2T(n/2)+n
总体时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
(4) 数据分析:
最终结果如下:


图像上符合$O(nlogn) $曲线,并且理论值与实际值误差较小。
5.问题思考
上述合并的方法是利用自下而上的遍历左右带中的点集,所以需要对带中的点以y坐标进行排序。
前提条件:左右区域内的点是依据y坐标进行排序的。
实际条件:左右区域内的点是依据x坐标进行排序的。(获取中轴线时,已排序)
所以每次递归的过程之中都需要对y进行排序。
对于均匀分布的大型点集,预计位于该带中的点的个数是非常少的。事实上,容易论证平均只有O(√n)个点是在这个带中的。
-----《数据结构与算法分析-C语言描述》P280
递推公式
平均情况
T
(
n
)
=
2
T
(
n
/
2
)
+
√
n
l
o
g
√
n
<
2
T
(
n
/
2
)
+
n
T(n) = 2T(n/2) + √nlog√n < 2T(n/2) + n
T(n)=2T(n/2)+√nlog√n<2T(n/2)+n
合并效率小于
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn),又因为一开始对x排序,
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)为时间效率下限。
总体时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
最坏情况
T
(
n
)
=
2
T
(
n
/
2
)
+
n
l
o
g
n
T(n) = 2T(n/2) + nlogn
T(n)=2T(n/2)+nlogn
总体时间复杂度
O
(
n
l
o
g
n
l
o
g
n
)
O(nlognlogn)
O(nlognlogn)
虽然最坏情况下为 O ( n l o g n l o g n ) O(nlognlogn) O(nlognlogn),但相较于 O ( n 2 ) O(n^2) O(n2)有较大提升。
为了解决这一问题,引入以下方法。
解决方案:
我们将保留两个表。一个按照x坐标排序,一个按照y坐标排序,成为P和Q。Pl和Ql传递给左半部分递归调用,Pr和Qr传递给右半部分递归调用。一旦分割线已知,我们依序转到Q,把每一个元素放入相应的Ql或Qr。容易看出,Ql和Qr将自动地按照y坐标排序。当递归调用返回时,我们扫描Q表并删除其x坐标不在带内的所有的点。此时Q只含有带中的点,而这些点保证是按照它们的y坐标排序的。
-----《数据结构与算法分析-C语言描述》P281
递推公式:
T
(
n
)
=
2
T
(
n
/
2
)
+
n
T(n) = 2T(n/2) + n
T(n)=2T(n/2)+n
总体时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
6.综合分析

显然,分治法的时间效率是要远远优于蛮力法。
每一次的优化,都对于时间效率有着小幅度的提升。
























 3815
3815











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










