几个著名而又非常有用的算法

算法案例:

主要有辗转相除法、更相减损术、秦九韶算法、k进制化十进制的算法。

辗转相除的定义：

所谓辗转相除法，就是对于给定的两个数，用较大的数除以较小的数。若余数不为零，则将余数和较小的数构成新的一对数，继续上面的除法，直到大数被小数除尽，则这时较小的数就是原来两个数的最大公约数。

更相减损术的定义：

就是对于给定的两个数，用较大的数减去较小的数，然后将差和较小的数构成新的一对数，再用较大的数减去较小的数，反复执行此步骤直到差数和较小的数相等，此时相等的两数便为原来两个数的最大公约数。

• 比较辗转相除法与更相减损术的区别：

  （1）都是求最大公约数的方法，计算上辗转相除法以除法为主，更相减损术以减法为主，计算次数上辗转相除法计算次数相对较少，特别当两个数字大小区别较大时计算次数的区别较明显。
  （2）从结果体现形式来看，辗转相除法体现结果是以相除余数为0则得到，而更相减损术则以减数与差相等而得到。

• 辗转相除法的一个程序算法的步骤：

  第一步：输入两个正整数m,n(m>n).
  第二步：计算m除以n所得的余数r.
  第三步：m=n,n=r.
  第四步：若r＝0,则m,n的最大公约数等于m；否则转到第二步.第五步：输出最大公约数m.

• 更相减勋术的一个程序算法步骤：

  第一步：输入两个正整数a,b(a>b);
  第二步：若a不等于b,则执行第三步；否则转到第五步；
  第三步：把a-b的差赋予r;
  第四步：如果b>r,那么把b赋给a,把r赋给b;否则把r赋给a，执行第二步；
  第五步：输出最大公约数b.

•  

  秦九韶算法：

  一般地，一元n次 多项式 的求值需要经过[n（n+1）]/2次 乘法 和n次 加法 ，而秦九韶算法只需要n次乘法和n次加法。在人工计算时，一次大大简化了运算过程。

  把一个n次多项式

  

  改写成如下形式：

  

  

  

  

  

  

  求 多项式 的值时，首先计算最内层括号内一次多项式的值，即

  

  

  然后由内向外逐层计算一次 多项式 的值，即

  

  

  

  

  这样，求n次 多项式 f(x)的值就转化为求n个一次多项式的值。

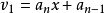
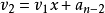
  结论：对于一个n次多项式，至多做n次 乘法 和n次加法。

  5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

  #include <bits/stdc++.h> using namespace std; class Solution { public:     int valueofPolynomial(string s)     {         int len = s.size();         int x, num[1000], dex = 0, temp = 0;         for (int i = 0; i < len; i++)         {             if (s[i] >= '0' && s[i] <= '9')             {                 temp = temp * 10 + s[i] - '0';             }             else if (s[i] == '+')             {                 temp = 0;                 continue;             }             else if (s[i] == '^')             {                 x = temp;                 continue;             }             else             {                 num[dex++] = temp;                 temp = 0;             }         }         temp = num[0];         for (int i = 1; i < dex; i++)         {             temp = temp * x + num[i];         }         return temp;     } }; int main() {     Solution Plain;     string str = "4*3^3+5*3^2+6*3^1+7*3^0";     cout << Plain.valueofPolynomial(str) << endl;     return 0; }

  以上就是秦九韶的完整代码。

  高斯消元法

  高斯消元法，是线性代数中的一个算法，可用来求解线性方程组，并可以求出矩阵的秩，以及求出可逆方阵的逆矩阵。
  高斯消元法的原理是：
  若用初等行变换将增广矩阵 化为 ，则AX = B与CX = D是同解方程组。
  所以我们可以用初等行变换把增广矩阵转换为行阶梯阵，然后回代求出方程的解。

  以上是线性代数课的回顾，下面来说说高斯消元法在编程中的应用。

  首先，先介绍程序中高斯消元法的步骤：
  (我们设方程组中方程的个数为equ，变元的个数为var，注意：一般情况下是n个方程，n个变元，但是有些题目就故意让方程数与变元数不同)

  1. 把方程组转换成增广矩阵。

  2. 利用初等行变换来把增广矩阵转换成行阶梯阵。
  枚举k从0到equ – 1，当前处理的列为col(初始为0) ，每次找第k行以下(包括第k行)，col列中元素绝对值最大的列与第k行交换。如果col列中的元素全为0，那么则处理col + 1列，k不变。

  3. 转换为行阶梯阵，判断解的情况。

  ① 无解
  当方程中出现(0, 0, …, 0, a)的形式，且a != 0时，说明是无解的。

  ② 唯一解
  条件是k = equ，即行阶梯阵形成了严格的上三角阵。利用回代逐一求出解集。

  ③ 无穷解。
  条件是k < equ，即不能形成严格的上三角形，自由变元的个数即为equ – k，但有些题目要求判断哪些变元是不缺定的。
      这里单独介绍下这种解法：
  首先，自由变元有var - k个，即不确定的变元至少有var - k个。我们先把所有的变元视为不确定的。在每个方程中判断不确定变元的个数，如果大于1个，则该方程无法求解。如果只有1个变元，那么该变元即可求出，即为确定变元。
  
  以上介绍的是求解整数线性方程组的求法，复杂度是O(n3)。浮点数线性方程组的求法类似，但是要在判断是否为0时，加入EPS，以消除精度问题。