浅谈欧拉回路与欧拉路径

§概念
欧拉环：图中经过每条边一次且仅一次的环；
欧拉路径：图中经过每条边一次且仅一次的路径；
欧拉图：有至少一个欧拉环的图；
半欧拉图：没有欧拉环，但有至少一条欧拉路径的图。

基图：对一个图而言把所有边视作无向边得到其基图。即将所有有向边变成无向边形成的无向图

  这里扯一点题外话，相信大家在小学课本里面都看到过一个叫做七桥问题的东西，好像是欧拉解决了这个问题，并且欧拉对一般情形也有深入的研究，所以一笔画问题的解决就是求图中的欧拉什么什么，名字貌似是这么来的。

  

§说明
感觉自己已经不会写Euler了，有些路径我早已忘记……所以决定写这么一个东西。当自己看到SGU101的时候，觉得自己好像只会写最简单的版本了！所以写了这个东西。

§各种情况【许多是参看以前的课件和旁边的链接】欧拉路径
【引理】
除了S、T之外的任何点一定满足进入次数等于出去次数！ 好吧，这个感觉就像一些奇怪的东西，待会儿会用到，先记住吧！

【无向图】
一个无向图是欧拉图当且仅当该图是连通的（注意，不考虑图中度为0的点，因为它们的存在对于图中是否存在欧拉环、欧拉路径没有影响）且所有点的度数都是偶数；一个无向图是半欧拉图当且仅当该图是连通的且有且只有2个点的度数是奇数（此时这两个点只能作为欧拉路径的起点和终点）；

证明：因为任意一个点，欧拉环（或欧拉路径）从它这里进去多少次就要出来多少次，故(进去的次数+出来的次数)为偶数，又因为(进去的次数+出来的次数)=该点的度数（根据定义），所以该点的度数为偶数。


【有向图】
一个有向图是欧拉图当且仅当该图的基图（这里同样不考虑度数为0的点）是连通的且所有点的入度等于出度；一个有向图是半欧拉图当且仅当该图的基图是连通的且有且只有一个点的入度比出度少1（作为欧拉路径的起点），有且只有一个点的入度比出度多1（作为终点），其余点的入度等于出度。

【混合图】
这个其实相当邪恶。

简直就是虐杀，超级丧病！我们先来看前面的【引理】，我开始提到了这是一个奇怪的东西，没错，感觉这个引理同【网络流】中的流量平衡/流守恒 (Flow Conservation)如出一辙。的确下面这个方法就用到了网络流的相关知识。

显然基图不连通肯定不是欧拉图
其实，难点在于图中的无向边，需要对所有的无向边定向（指定一个方向，使之变为有向边），使整个图变成一个有向欧拉图（或有向半欧拉图）。若存在一个定向满足此条件，则原图是欧拉图（或半欧拉图）否则不是。关键就是如何定向？


首先给原图中的每条无向边随便指定一个方向（称为初始定向），将原图改为有向图G'，然后的任务就是改变G'中某些边的方向（当然是无向边转化来的，原混合图中的有向边不能动）使其满足每个点的入度等于出度。
设D[i]为G'中(点i的出度 - 点i的入度）。可以发现，在改变G'中边的方向的过程中，任何点的D值的奇偶性都不会发生改变（设将边<i, j>改为<j, i>，则i入度加1出度减1，j入度减1出度加1，两者之差加2或减2，奇偶性不变）！而最终要求的是每个点的入度等于出度，即每个点的D值都为0，是偶数，故可得：若初始定向得到的G'中任意一个点的D值是奇数，那么原图中一定不存在欧拉环！


若初始D值都是偶数，则将G'改装成网络：设立源点S和汇点T，对于每个D[i]>0的点i，连边<S, i>，容量为D[i]/2；对于每个D[j]<0的点j，连边<j, T>，容量为-D[j]/2；G'中的每条边在网络中仍保留，容量为1（表示该边最多只能被改变方向一次）。求这个网络的最大流，若S引出的所有边均满流，则原混合图是欧拉图，将网络中所有流量为1的中间边（就是不与S或T关联的边）在G'中改变方向，形成的新图G''一定是有向欧拉图；若S引出的边中有的没有满流，则原混合图不是欧拉图。


为什么能这样建图？
考虑网络中的一条增广路径S-->i-->...-->j-->T，将这条从i到j的路径在G'中全部反向，则：i的入度加1出度减1，j的入度减1出度加1，路径中其它点的入度出度均不变。而i是和S相连的，因此初始D[i]>0，即i的出度大于入度，故这样反向之后D[i]减少2；同理，j是和T相连的，这样反向之后D[j]增加2。因此，若最大流中边<S, i>满流（流量为初始D[i]/2），此时D[i]值就变成了0，也就是i的入度等于出度。因此只要使所有S引出的边全部满流，所有初始D值>0的点的D值将等于0，又因为将边变向后所有点的D值之和不变，所有初始D值小于0的点的D值也将等于0，而初始D值等于0的D点既不与S相连也不与T相连，所以它们是网络中的中间点，而中间点的流入量等于流出量，故它们的入度和出度一直不变，即D值一直为0。因此，整个图G'成为欧拉图。


（2）欧拉路径的判定：
首先可以想到的是枚举欧拉路径的起点i和终点j，然后在图中添加边<j, i>，再求图中是否有欧拉回路即可。但是，该算法的时间复杂度达到了O(M * 最大流的时间)，需要优化。
前面已经说过，在将边变向的过程中任何点的D值的奇偶性都不会改变，而一个有向图有欧拉路径的充要条件是基图连通且有且只有一个点的入度比出度少1（作为欧拉路径的起点），有且只有一个点的入度比出度多1（作为终点），其余点的入度等于出度。这就说明，先把图中的无向边随便定向，然后求每个点的D值，若有且只有两个点的初始D值为奇数，其余的点初始D值都为偶数，则有可能存在欧拉路径（否则不可能存在）。进一步，检查这两个初始D值为奇数的点，设为点i和点j，若有D[i]>0且D[j]<0，则i作起点j作终点（否则若D[i]与D[j]同号则不存在欧拉路径），连边<j, i>，求是否存在欧拉环即可（将求出的欧拉环中删去边<j, i>即可）。这样只需求一次最大流。

【小结】

其实图论算法本身并不是非常的可怕，大部分的代码都有成品可以大肆利用。但是图论最重要的应该是在建模方面：

下面来看坑了蒟蒻我的SGU101

额，题目大意是什么domino，英语蒟蒻的我看了一天才知道是多米诺。

多米诺骨牌，一种用小的方的木块或其他材料，每个都被一些点在面上标记，这些木块通常被称为骨牌。每个骨牌的面都被一条线分成两个方形，两边各有一定点数。N个多米诺骨牌，每个骨牌左右两侧分别有一个0~6的整数（骨牌可以旋转以调换其左右两数），求一种把这些骨牌从左到右排列的方案，使得所有相邻的两数字相等（即左边骨牌右侧的数字等于右边骨牌左侧的数字）。

题目值得思考，中点在于如何构造边和点：

 将0~6这7种牌面看作节点，把骨牌看作是连接两节点的无向弧，这样就组成了一个无向图（当然可能有重边），图中的一条欧拉路就对应一种方案。
   欧拉路的构造方法：若图连同且度为奇数的节点不超过两个，则可以构造出欧拉路。先选一个度为奇数的节点（若没有就任选一个度为偶数的节点），以该节点为起点，深搜遍历所有的弧（每条弧只遍历一次），在每次回溯时将当前弧记录下来，记录的弧的排列就组成了一条欧拉路。
   实际编程时，为便于输出方案，可将图中的边加上一个“权值”，为骨牌的编号。

蒽，大体就是如此。感觉我还是水了。

对于我WA过的数据进行解释

[WA]
test 5 呵呵自动把编号当做是否要反转，这也能过前面的点我也是醉了
test 1 对于这一块而言下一块的反转应该与这一块不同。。。

【补例】

下面这道题是ACM的某题，也考虑到了构图是边和点的选择从而导致图的不同

有N个盘子，每个盘子上写着一个仅由小写字母组成的英文单词。
你需要给这些盘子按照合适的顺序排成一行，使得相邻两个盘子中，前一个盘子上面单词的末字母等于后一个盘子上面单词的首字母。
请你编写一个程序，判断是否能达到这一要求。如果能，请给出一个合适的顺序。

【模型1】

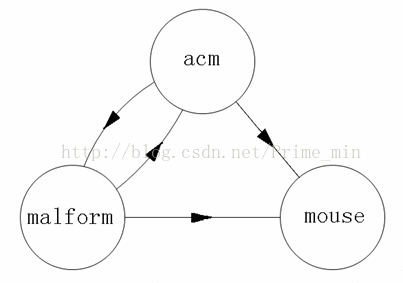
将每个盘子看作一个顶点。
如果盘子B能连接在盘子A后面，那么从A向B连一条有向边。

问题转化为在图中寻找一条不重复地经过所有顶点的路径，即哈密尔顿路。
但是，求哈密尔顿路是一个十分困难的问题，岂止是困难，简直是吓人，这样的建模没有给解题带来任何便利。我们必须另辟蹊径。

【模型2】

当然模型2 就应运而生。

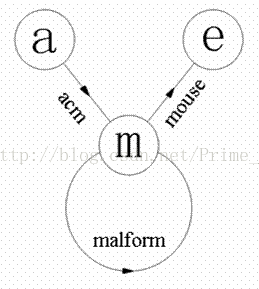
以26个英文字母作为顶点。
对于每一个单词，在图中从它的首字母向末字母连一条有向边。

然后求欧拉路径就可以了。

好吧。这只是一个浅析，我毕竟大概确实是一个蒟蒻。希望大家能看懂。