图像处理：阈值法与K-means聚类在图像分割中的应用-CSDN博客

本文链接：https://blog.csdn.net/programing_game/article/details/135100764

1.阈值法

（1）基本思想：

根据灰度图像直方图的特点，以直方图双峰之间的谷底处的灰度值作为阈值进行图像处理，能够较好地分割目标区域。

在图像分割的过程中，阈值选的过大或者过小都会大大影响分割的效果，所以，在使用阈值分割的过程中，阈值的选择很重要，使用直方图的方法不容易确定出合适的阈值，常见的阈值分割方法有大津算法（Ostu）、迭代阈值法、自适应阈值分割、最大熵阈值分割等。

迭代寻找最佳阈值的算法思想

1) 设定参数T0=0.01，并选择一个初始的估计阈值T1。

2)用阈值T1分割图像。将图像分成两部分: G1前景是由灰度值大于T1的像素组成，G2背景是由灰度值小于或等于T1的像素组成。

3)计算G1和G2中所有像素的平均灰度值u1和u2，以及新的阈值T2 =(u1+u2)/2。

4)如果|T2-T1|<T0，则推出T2即为最优阈值；否则，将T2赋值给T1，并重复步骤2)—4)，直到获取最佳阈值。

（2）代码实现（直方图法和迭代阈值法）

①直方图法

img = imread('yx.png');

I = rgb2gray(img); %灰度处理

K = im2double(I); %归一化

[h,w] = size(I);

imhist(I) %灰度直方图

pause(3)

for i = 1:h

for j =1:w

if( K(i,j) > 199/255)

K(i,j) = 1; % 将大于全局阈值的像素点置为1(白色)

else

K(i,j) = 0; % 将小于等于全局阈值的像素点置为0(黑色)

end

% imshow(K);

% K = im2bw(I,199/255); %根据直方图观察得到阈值为199/255

%graythresh(I)返回Otsu算法求解后的阈值为0.6118

subplot(1,2,1);

imshow(I);

subplot(1,2,2);

imshow(K);

灰度直方图分割结果

②迭代阈值法

img = imread('yx.png');

I = rgb2gray(img); %灰度处理

I = im2double(I); %归一化

T0 = 0.01;

T1 = (min(I(:))+max(I(:)))/2;

r1 = find(I>T1);

r2 = find(I<=T1);

T2 = (mean(I(r1))+mean(I(r2)))/2;

if(abs(T2-T1) < T0)

K = im2bw(I,T2);

else

while(abs(T2-T1) >= T0)

T1 = T2;

r1 = find(I>T1);

r2 = find(I<=T1);

T2 = (mean(I(r1))+mean(I(r2)))/2;

end

K = im2bw(I,T2);

end

subplot(1,2,1);

imshow(I);

title('原灰度图像');

subplot(1,2,2);

imshow(K);

title(['迭代最佳阈值为 ',num2str(T2)]);

2.K-means聚类

（1）基本思想

输入：①n个d维数据的特征向量D=(x1,x2,x3,…xn);②聚类的簇数K。

输出：每个数据所属的聚簇标签（簇划分）C=C1,C2,…,CK

初始聚类中心向量V=(v1,v2,…,vk)T。根据输入的参数k，将数据划分成k个簇，即k个聚类中心，在每一轮迭代中，依据k个聚类中心将周围的点分别组成k个簇，而重新计算的每个簇的质心（即簇中所有点的平均值，也即几何中心）将被作为下一轮迭代的参照点。迭代使得选取的参照点越来越接近真实的簇质心，所以目标函数越来越小，聚类效果越来越好。

采用误差平方和准则函数作为聚类准则函数，误差平方和准则函数定义为：

Jc=i=1kp∈Ci||p-Mi ||2

其中，Mi是类Ci中数据对象的均值，p是类Ci中的空间点

（2）算法步骤：

①初始化聚类质心

随机选择K个样本作为初始聚类质心c={c1,c2,…,cK}，每个聚类质心cj所在的集合记为Gj。

②根据欧式距离对数据进行聚类

将每个待聚类的数据放入唯一一个聚类集合中。

计算xi和cj之间的欧式距离：

distxi,cj=m=1d(xi,m-cj,m)2

(1≤i≤n,1≤j≤K)

将每个xi放入与之距离最近的聚类质心所在聚类集合中。

③更新聚类质心

cj=1|Gj|xi∈Gjxi

根据聚类结果更新聚类质心，即根据每个聚类集合中所包含的数据，求均值得到该聚类集合新的质心。

④重复②③步，直到收敛。

聚类迭代终止判断一般说来有以下两种：

a.已经达到了迭代次数的上限；

b.前后两次迭代中，聚类质心保持不变。

（3）代码实现（matlab）

img = imread('yx.png');

I = rgb2gray(img); %灰度处理

I = im2double(I); %归一化

k=2;

[h,w] = size(I);

R = zeros(size(I)); %分割后的结果

label =zeros(h,w); %类别矩阵

C = zeros(k,1); %聚类中心向量

newcenter = zeros(k,1);%更新聚类中心向量

error = 10e-4; %无穷小

iter = 0 ;%迭代次数

%初始化聚类中心

for i =1:k

h_rand = randi(h);

w_rand = randi(w);

C(i,:) = I(h_rand,w_rand);

end

%聚类

while true

iter =iter +1;

D = zeros(k,1);

s = zeros(1,k);

num=zeros(1,k);

for i = 1:h

for j = 1:w

for x =1:k

D(x,:)= abs(I(i,j)-C(x,:));

end

[~,temp] = min(D); %temp返回距离最小值的行坐标索引

label(i,j) = temp;

end

%统计各类的数目和像素的总和

for i = 1:h

for j = 1:w

for x =1:k

if(label(i,j) ==x)

s(1,x) = s(1,x)+I(i,j);

num(1,x) = num(1,x)+1;

end

%更新聚类中心

for x =1:k

newcenter(x,1) = s(1,x)/num(1,x);

end

% 当簇中心变化很小时退出循环

if(abs(min(newcenter)-min(C))<error)

break;

else

C=newcenter;

end

if(iter == 10)

break;

end

%图像分割

for i =1:h

for j =1:w

for x =1:k

if(label(i,j) ==x)

R(i,j) = C(x);

end

figure

subplot(121),imshow(I);

subplot(122),imshow(R);

title(['k=',num2str(k)]);

（4）运行结果

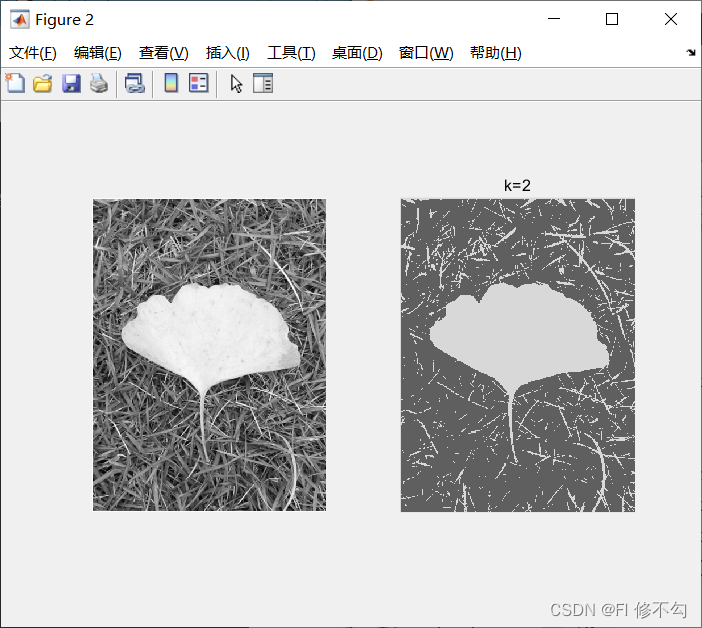
聚类中心向量为[0.85,0.37],乘255为[217,94]

补充：使用matlab自带函数imsegkmeans进行分割

img = imread('yx.png');

I = rgb2gray(img); %灰度处理

[L,Centers] = imsegkmeans(I,2); %K-means聚类

B = labeloverlay(I,L);

imshow(B)

title("Result")

进一步验证聚类中心向量为

[97,216]，与上述代码所得结果一致。

3.思考及总结

本次采用了阈值法和K-means聚类对图像进行分割，阈值法原理较容易理解，关键在阈值的选取，K-means作为机器学习中无监督学习的一种，原理相对通俗易懂，容易实现，虽然是局部最优，但效果往往不错；至于缺点，由于所给图片前景和背景较为确定，所以K值的选取事先确定，多数情况由于不知道要分成几类，聚类数目K值的选取需要事先确定，初始聚类中心向量的选择也会影响最终的聚类效果。此外，算法是迭代执行，时间开销比较大。