最短路径算法

 

 

 

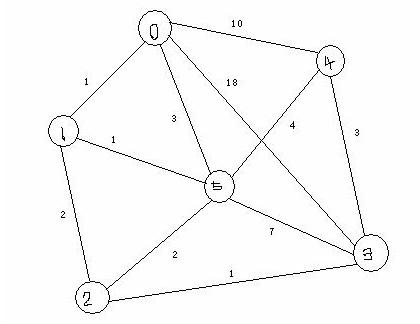
Floyd算法

          0        1         2        3        4        5

 

0        0        1        ∞       ∞      5        4

1        1        0         8        ∞      ∞      1

2       ∞       8         0        1        ∞      3

3       ∞      ∞        1        0        3        5 

 

4       5        ∞       ∞       3        0        2

 

5       4         1        3         5        2        0

Floyd算法过程描述如下：
　　１、 首先Ｓ以边集Ｍ初始化，得到所有的直接连通代价；
　　２、 依次考虑第k个结点，对于Ｓ中的每一个Ｓ[i][j]，判断是否满足：
　　S[i][j]>S[i][k]+S[k][j]，如果满足则用S[i][k]+S[k][j]代替Ｓ[i][j]，此为第k步；
　　３、 k循环取遍所有结点，算法结束时，Ｓ为最终解。

#include <stdio.h>

#include <stdlib.h>

main()

{int i,j,k,temp,number,a[6][6],d[6][6],r[6][6];

 k=0;number=0;

 for(i=0;i<6;i++)

    for(j=0;j<6;j++)

      {printf("a[%d][%d]=",i,j);

       scanf("%d",&temp);

       a[i][j]=temp;

       }

 for(i=0;i<6;i++)

    for(j=0;j<6;j++)

    {printf("a[%d][%d]=%d   ",i,j,a[i][j]);

     if(j==6-1) printf("/n");

     }

for(i=0;i<6;i++)

    for(j=0;j<6;j++)

      {

       d[i][j]=a[i][j];

       r[i][j]=a[i][j];

       }

while(number<6)

{

 for(i=0;i<6;i++)

  for(j=0;j<6;j++)

    for(k=0;k<6;k++)

     if(d[i][k]+d[k][j]<d[i][j])

     {

      d[i][j]=d[i][k]+d[k][j];

      r[i][j]=d[i][j];

     }

 number=number+1;

 }

for(i=0;i<6;i++)

   for(j=i+1;j<6;j++)

    printf("r[%d][%d]=%d/n ",i,j,r[i][j]);

 getch();

}

 

r[0][1]=1

r[0][2]=5

r[0][3]=6

r[0][4]=4

r[0][5]=2

r[1][2]=4

r[1][3]=5

r[1][4]=3

r[1][5]=1

r[2][3]=1

r[2][4]=4

r[2][5]=3

r[3][4]=3

r[3][5]=4

r[4][5]=2

 

 

 

 

 

 

1　经典Dijkstra算法的主要思想

  算法介绍
Dijkstra算法是由荷兰计算机科学家艾兹格·迪科斯彻发现的。算法解决的是有向图中最短路径问题。

举例来说，如果图中的顶点表示城市，而边上的权重表示著城市间开车行经的距离。 Dijkstra算法可以用来找到两个城市之间的最短路径。

Dijkstra算法的输入包含了一个有权重的有向图G，以及G中的一个来源顶点S。 我们以V表示G中所有顶点的集合。 每一个图中的边，都是两个顶点所形成的有序元素对。(u,v)表示从顶点u到v有路径相连。 我们以E所有边的集合，而边的权重则由权重函数w: E → [0, ∞]定义。 因此，w(u,v)就是从顶点u到顶点v的非负花费值(cost)。 边的花费可以想像成两个顶点之间的距离。任两点间路径的花费值，就是该路径上所有边的花费值总和。 已知有V中有顶点s及t，Dijkstra算法可以找到s到t的最低花费路径(i.e. 最短路径)。 这个算法也可以在一个图中，找到从一个顶点s到任何其他顶点的最短路径。

算法描述
这个算法是通过为每个顶点v保留目前为止所找到的从s到v的最短路径来工作的。初始时，源点s的路径长度值被赋为0（d[s]=0）， 同时把所有其他顶点的路径长度设为无穷大，即表示我们不知道任何通向这些顶点的路径（对于V中所有顶点v除s外d[v]= ∞）。当算法结束时，d[v]中储存的便是从s到v的最短路径，或者如果路径不存在的话是无穷大。 Dijstra算法的基础操作是边的拓展：如果存在一条从u到v的边，那么从s到u的最短路径可以通过将边(u,v)添加到尾部来拓展一条从s到v的路径。这条路径的长度是d+w(u,v)。如果这个值比目前已知的d[v]的值要小，我们可以用新值来替代当前d[v]中的值。拓展边的操作一直执行到所有的d[v]都代表从s到v最短路径的花费。这个算法经过组织因而当d达到它最终的值的时候没条边(u,v)都只被拓展一次。

算法维护两个顶点集S和Q。集合S保留了我们已知的所有d[v]的值已经是最短路径的值顶点，而集合Q则保留其他所有顶点。集合S初始状态为空，而后每一步都有一个顶点从Q移动到S。这个被选择的顶点是Q中拥有最小的d值的顶点。当一个顶点u从Q中转移到了S中，算法对每条外接边(u,v)进行拓展。  

　　

#include "stdio.h"

struct vertex

{

 int name;

 int tag;

 };

 

main()

{

 int i,j,k,t,kt,temp,tag_number,min;

 struct vertex s[6];

 int dist[6],a[6][6],path[6][6];

 for(i=0;i<6;i++)

   for(j=0;j<6;j++)

   {

    printf("a[%d][%d]=",i,j);

    scanf("%d",&a[i][j]);

    }

 

 for(i=0;i<6;i++)

   dist[i]=a[0][i];

 

 for(i=0;i<6;i++)

   for(j=0;j<6;j++)

      path[i][j]=-1;

 

 for(i=0;i<6;i++)

   {

    s[i].name=i;

    s[i].tag=0;

    }

 

 s[0].tag=1;

 path[0][0]=0;

 tag_number=1;

 

 while(tag_number<6)

   {

    for(i=0;i<6;i++)

     {

      if(s[i].tag==0)

       {

        for(j=0;j<6;j++)

          if((s[j].tag==1)&&(dist[j]+a[j][i]<dist[i]))

         dist[i]=dist[j]+a[j][i];

        }

     }

    min=100;

    for(k=0;k<6;k++)

     {

      if((s[k].tag==0)&&(dist[k]<min))

      {

       min=dist[k];

       t=k;

       }

     }

 

   dist[t]=min;

   s[t].tag=1;

   printf("The vertex %d has been selected!/n",t);

   k=t;

   temp=0;

   for(i=0;i<6;i++)

       if((s[i].tag==1)&&(i!=k)&&(dist[k]==dist[i]+a[i][k]))

       {

        while(path[i][temp]!=-1)

        temp++;

        kt=j=0;

         for(kt=0;kt<temp;kt++)

         {

          path[k][kt]=path[i][j];

          j++;

         }

        path[k][kt]=k;

       }

   tag_number++;

 

   }

 

 for(i=0;i<6;i++)

    printf("dist[%d]=%d/n",i,dist[i]);

 

 for(i=0;i<6;i++)

   for(j=0;j<6;j++)

    if(path[i][j]!=-1)

      printf("path[%d][%d]=%d ",i,j,path[i][j]);

    else

      printf("/n");

 

 getch();

 

}

 

dist[0]=0

dist[1]=1

dist[2]=3

dist[3]=4

dist[4]=6

dist[5]=2

path[0][0]=0 

path[1][0]=0 path[1][1]=1 

path[2][0]=0 path[2][1]=1 path[2][2]=2 

path[3][0]=0 path[3][1]=1 path[3][2]=2 path[3][3]=3 

path[4][0]=0 path[4][1]=1 path[4][2]=5 path[4][3]=4 

path[5][0]=0 path[5][1]=1 path[5][2]=5