机器学习基本概念2

一、认识线性模型的局限性

我们可以通过改变线性模型（y = b + wx）w，b可以得到不同的图形，但是它永远是一条直线，这种局限性我们把它称之为Model Bias，如果我们的实际图形是一条折线或者曲线，那么线性模型就无法表示。这个时候我们就需要一条更加灵活的模型。

二、找一个新的函数。

1. 引入：折线图的表示

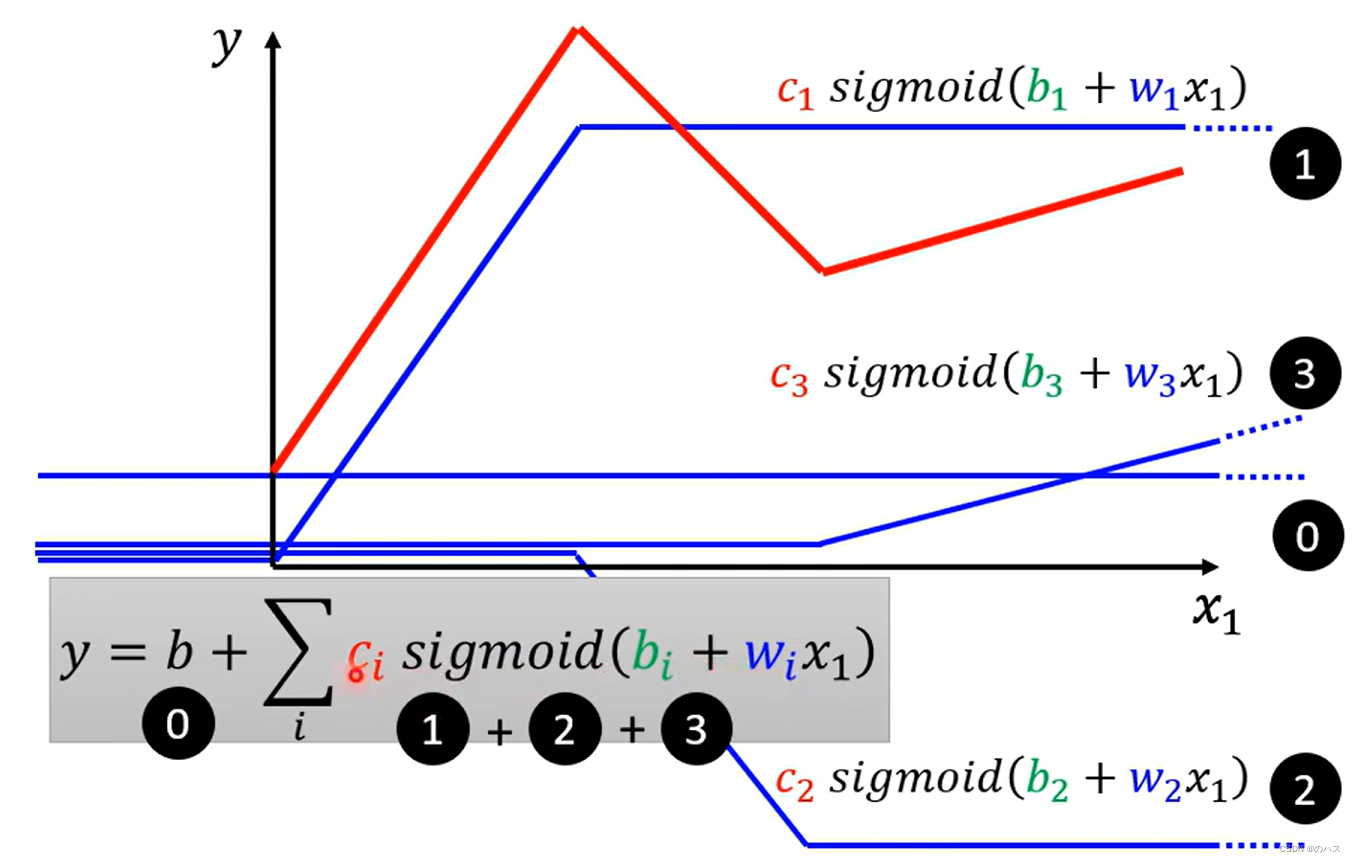
图中的红线是由一个常数和多个蓝色函数（在两个转折点之间有与红线对应区间平行的线段，其它地方是平的）相加得到的，我们用 函数 0
来表示这个常数，对于每一段线段，我们各用一个函数与之前的所有函数相加，如图中红线第一段上升，我们用一个函数 1与之前的函数0相加来表示，同理红线第一个转折点之后的下降线段，用函数 2与函数0，函数1相加来表示，以此类推。

折线图都能用思想这种方式来表示，折线转折点越多，需要的蓝色函数也就越多。当数量趋近于无穷时，近似的可以用来表示曲线，和微积分是一个思想。

那么如何来表示这个蓝色函数呢？

近似表示蓝色函数的方法一

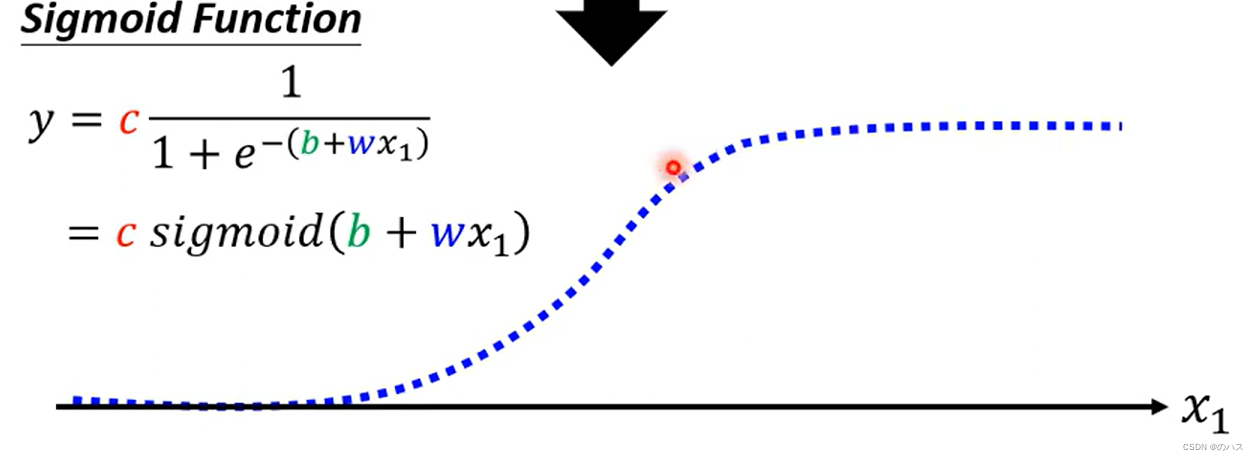
我们采用一个Sigmoid Function，可以理解成一个S型的函数来近似表示这个蓝色函数（这种折线不平滑的函数称为Hard Sigmoid）。

改变这三个变量时函数变化：
改变w：改变坡度

改变b：左右移动函数

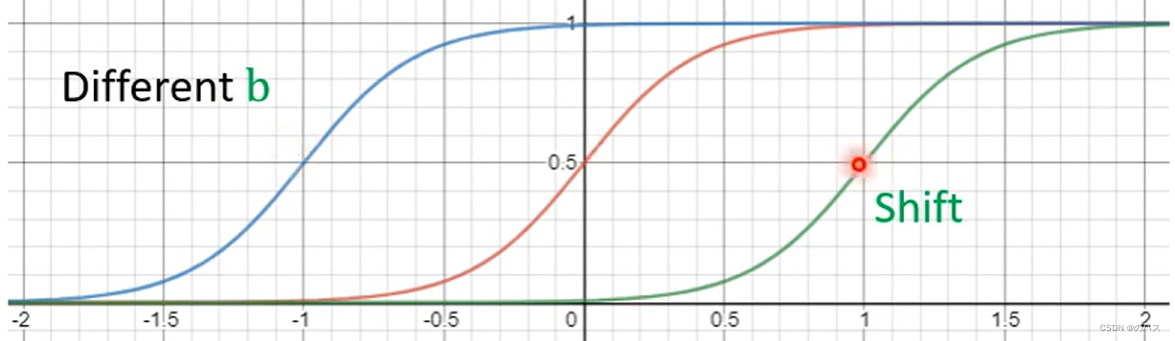
改变c：改变函数高度

用Sigmoid函数表示之后，折线图可以用这样的模型表示：

蓝色函数的表示方法二

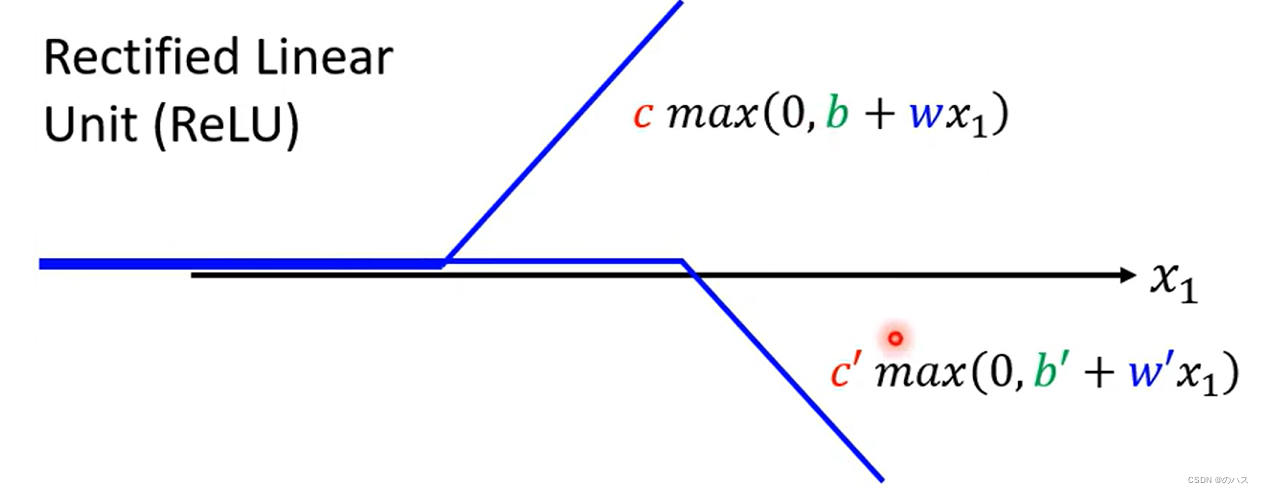
我们也可以使用一个ReLU函数来近似表示我们的蓝色函数，max函数表示取0和函数b+wx中大的那个表示在图上。用这样两条函数来表示我们的蓝色函数。

我们取更多的features可以得到：

由于我们的ReLU函数是由两条函数合成的，我们需要Sigmoid函数两倍的参数。
这两种近似表示蓝色函数的函数（Sigmoid max）我们称之为Activation function。
两种之中max函数会好一点

3.Step1.写一个带有未知参数的函数

括号里的内容可以表示为矩阵乘法：

同理，我们用相同的方式将y表示出来。


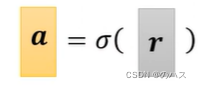
表示用一个函数c塔，将r转变为a

4.Step2.定义Loss函数

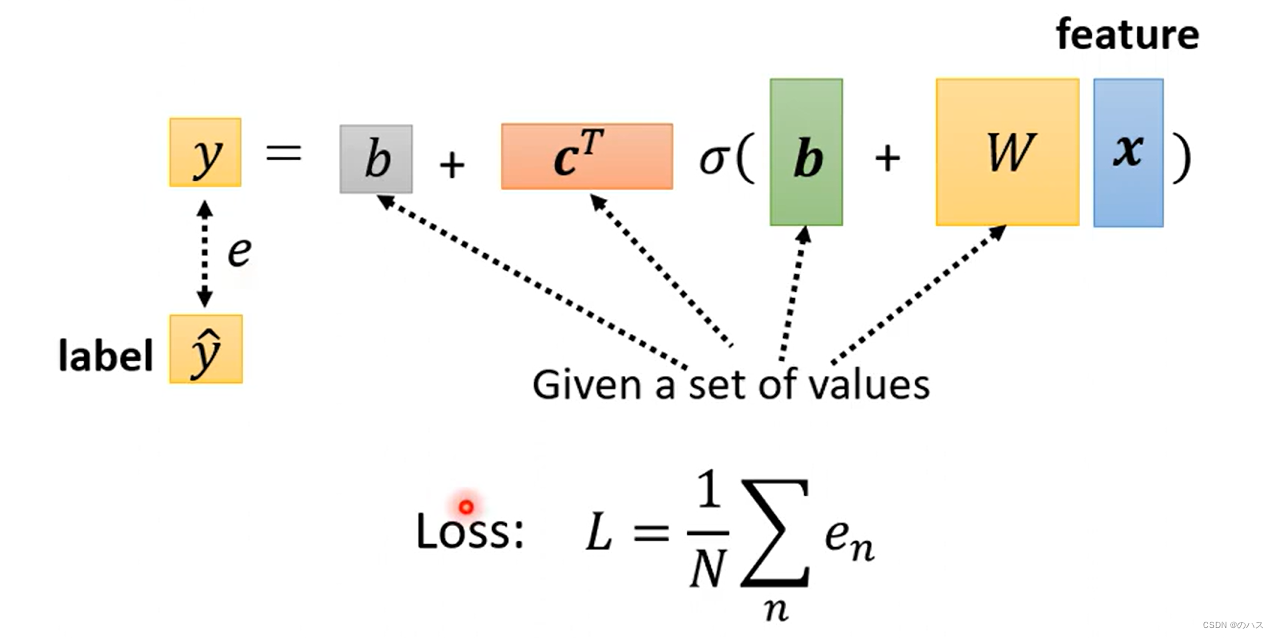
同上次讲的，给定一组参数的值，然后带入已知的feature值，算出的实际y与label的误差，最后算出L值。

5.Step3.最优化

我们把未知参数全部用c塔来表示。


对于取得最小L值的一组c塔我们称为c塔*。
最优化方法也和线性模型类似，我们先随机找一个c塔0，在这个位置L对c塔求微分得到梯度。
然后用c塔0 减去我们之前定义的Learning Rate乘以梯度得到c塔1，以此类推。

还有另一种方法来更新：
我们把所有的c塔，随机分为很多个batch，然后去每个batch中的c塔计算一次梯度，用这个梯度来更新c塔，每个batch算一次，当所有batch都进行了一次之后，我们称之为一个epoch。

epoch的理解：

由于每个batch就需要更新一次，所以一个epoch更新的次数等于batch数。

6.神经网络和深度学习

我们可以用同样的方法，再给一组参数得到a’，这样通过迭代的方式来减小我们的L值


我们把一个r称之为一个Neuron，很多Neuron组成的网络，这就是我们常说的神经网络（Neural Network）。
相同层次的Neruon我们称之为一个hidden layer
很多的layer就意味着Deep 这也就是我们所谓的深度学习（Deep Learning）

但是层数增多也可能会出现问题，对于这种training data 数值变好，但预测数据数值变差的现象，我们称为Overfitting