题意:
给你a数组,然后要得到一个b数组,b数组中的每一项是a中那一项和其前面的很多项异或的结果。
但是这个操作要重复m次。
关于题意有几种说法:
1.a中的第i个元素异或完前边的之后,结果替换a[i],也就是你得到a[i]之前,a[i]前面的元素都在变
2.a中的第i个元素异或完前边的之后,a[i]不变,把结果给了b[i],一直到a中第n个元素有了结果并给了b[n]之后,直接把b数组看成是a数组,也就是你得到a[i]之前,a[i]前面的元素都没变
两种说法都可过样例,但是正确的题意是第二种,第一种看似也没毛病,而且做的时候过程也很经典。
先说正解:
变化过程如上,把系数提取出来之后发现每一项是它左边和上边的加起来得到的,类似一个杨辉三角
(其中a前面的系数表示有几个a相异或)。然后发现系数可写成下面这样:
倒着看,每一项里的第几个就是前多少项对应着的。
那么根据行标列标的关系,也就是上图右边,可得每个位置的组合数是
(第m次变化,第i项) C(m+i-2,i-1)
然后一个数经过奇数次异或等于自己,经过偶数次异或等于0,那么需要判断组合数的奇偶性。
判断组合数的奇偶:C(n,m),如果n&m==m则C(n,m)为奇数
然后用一个巧妙的循环把上面的结论综合一下就ok了。
#include <bits/stdc++.h>
using namespace std;
int a[250050],b[250050];
int main()
{
int t,m,n;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)///这层循环遍历系数
{
int aa=i+m-2;
int bb=i-1;
if((aa&bb)==bb)///对每一项的系数判断,奇数为本身,偶数是0(无操作)
for(int j=i;j<=n;j++) /// 这层循环对b进行求值,类似于一个直角倒三角赋值
b[j]=b[j]^a[j-i+1];///j-i+1表示b[j]的倒数第几项
}
for(int i=1;i<n;i++)
printf("%d ",b[i]);
printf("%d\n",b[n]);
}
return 0;
}









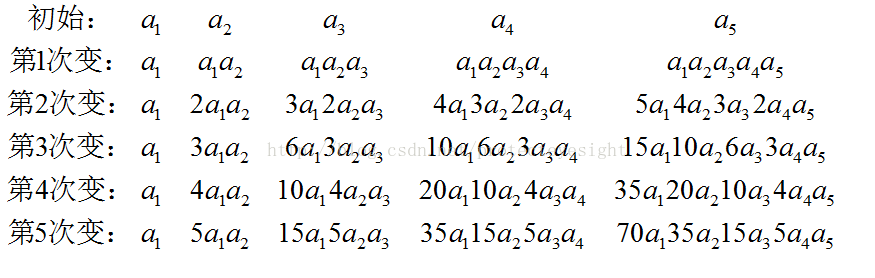


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








