列表错题本

概念题：

1.如果有一个列表 list1，有两种方法可以获取到该列表的最后一个元素，你知道分别是什么吗？

答：list1[len(list1) - 1]    和   list1[-1]1:Yka
^zsg4exIZ-w6jX2H$7) 9c},k(L+
解析：使用下标索引的方式可以实现列表的随机访问（就是你想访问哪个元素就访问哪个）。(>0o&h4lC
dKxAOm}MWD?$T+|G`BSqv:p>3J~Y2
这第一种方法是先使用 len() 函数计算列表的长度，然后 -1 是因为下标索引值是从 0 开始数起的。@9dfE
`mN^cCh)@p*QEK2ObeV{
第二种方法看上去更加 “老司机”，因为你知道 Python 是允许反向索引的，下标值为 -1，则表示直接访问最后一个元素。

2.请问下面代码打印的结果是什么？

[1, 2, 3, 4, 5][:3]

正解：[1,2,3] 

3.请问下面代码打印的结果是什么？

[5, "上", 4, "山", 3, "打", 2, "老", 1, "虎"][-2::-2]

正解：首先，切片操作 [::-1] 是将列表前后翻转：

[5, "上", 4, "山", 3, "打", 2, "老", 1, "虎"][::-1]
['虎', 1, '老', 2, '打', 3, '山', 4, '上', 5]

然后，将跨度值设置为 2（[::2]）代表每提取一个元素，就跨过下一个元素，那么设置为 -2（[::-2]）就表示提取的顺序是带跨度的倒着来：

[5, "上", 4, "山", 3, "打", 2, "老", 1, "虎"][::-2]
['虎', '老', '打', '山', '上']

最后，既然是倒着来，我们设置它的起始元素为倒数第二个，所以结果就是 [1, 2, 3, 4, 5]： 

[5, "上", 4, "山", 3, "打", 2, "老", 1, "虎"][-2::-2]
[1, 2, 3, 4, 5]

3. 下面有两列表，请问如何将 list2 列表中的全部元素，添加到 list1 列表中第 2 和第 3 个元素的中间。

list1 = [1, 2, 8, 9]
list2 = [3, 4, 5, 6, 7]

 正解：利用切片大法

list1 = list1[:2] + list2 + list1[2:]
list1
[1, 2, 3, 4, 5, 6, 7, 8, 9]

4.请问 == 运算符和 is 运算符有什么区别呢？

== 运算符用于判断两个变量的值是否相等，而 is 运算符用于判断两个变量是否为同一对象。 

5.请问下面代码的执行结果是？

>>> len([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

[[1, 2, 3], [4, 5, 6], 7, 8, 9]

6. 请问下面代码的执行结果是？

>>> len([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

 正解：3

7.请问下面代码的结果是返回 True 还是 False 呢？

>>> a = 1000
>>> b = 1000
>>> a is b

出于性能优化方面的考虑，Python 在内部为 -5~256 范围内的整数维护了一个数组，起到缓存的作用。hAS:U
ev2b#6qQ9z{&oxN!R0my^uh?gnrO
这样，每次你试图创建一个 -5~256 范围内的整数时，Python 都会从这个数组中返回相对应的引用，而不是重新开辟一块新的内存空间存放。

但是，如果超过了 -5~256 这个范围（大家可以自己动手测试一下），比如 1000，那么 Python 会为两个 1000 单独开辟两块不同的内存区域，因此 a is b 的结果为 False。 

8.请问如何不直接使用下标索引值的前提下，将下面列表中的 “黑寡妇“ 替换为 ”神奇女侠“？ 

>>> heros = ['蜘蛛侠', '绿巨人', '黑寡妇', '鹰眼', '灭霸', '雷神']

heros[heros.index("黑寡妇")] = "神奇女侠", 

9.. 请问你是如何理解 ”在 Python 中，变量不是盒子” 这句话的？Lj9s@mWX+
DuZ!(Fv7odL$,E{:j"9?O+A i_n-
答：在一些编程语言中，经常会有“变量就是盒子”这样的比喻，因为赋值操作就像是往盒子里面放东西。j>9AG%U
%rm*WQV;ZqdA(+8:~F1e$
但在 Python 中变量并不是一个盒子，当赋值运算发生的时候，Python 并不是将数据放进变量里面，而是将变量与数据进行挂钩，这个行为我们称之为引用。

10.请问下面代码执行后，y 的值是多少

>>> x = 1
>>> y = x
>>> x = 2

1。来自：
wn%U:[^cKRk$.#{'VmlQb|aIJ
解析：这个例子跟视频中演示的可不是一个性质的东西。IY4X_
c-[ty~QG!^:U$}9T<R`oF8b3iY
前两个语句执行后，内存中的情况是这样的：[Y*jMbt
f$Twtg8 @.3bmz0d]lZ:
 

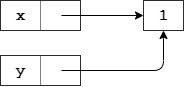
*(9`iCpg?{R0,=<s#e|wZ
第三个语句将 x 赋值为 2，也就是将其原来指向 1 的引用改为数字 2 的引用了：t[HBe
WKOb<uJ`4*:U^p5mxolr#_$|ABqPE
 

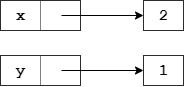
%'~@f*OI78X(DQ;#W`e)Ro5n.3lEh
如果你们不嫌我啰嗦，小甲鱼再讲两句。来自：
W O1E80YFC#xyN~(QBA|}5
视频中演示的是将两个变量指向同一个列表，然后通过下标来修改列表中的元素的值，改的是列表的内容，而非变量的引用，才会牵一发而动全身。,z

11.请问下面代码执行后，列表 x 和 y 的内容分别是什么？ostv#{*9
dHiZyBuAJbDs~S*T_14'N

>>> x = [[1, 2, 3], [4, 5, 6]]
>>> y = x.copy()
>>> y.append(7)
>>> y[1].append(8)

 答：代码执行后，列表 x 变成 [[1, 2, 3], [4, 5, 6, 8]]，列表 y 变成 [[1, 2, 3], [4, 5, 6, 8], 7]。B5,X401EAD
"A&(cEh0rqIwiWeH!-z<nfg.K D@y
解析：来自：
=s;m(BJ9'~2z1>!j?$aZW:CAlQkLG%
调用列表的 copy() 方法实现的是浅拷贝，浅拷贝，只能拷贝第一层数据，其余仅拷贝其引用。5)l{tnsq&W
U4f[]G.nmCtArO%5!,@b<alPh-oT
y.append(7) 是往列表 y 添加一个新元素 7，这一步操作对列表 x 并不会产生任何影响；4os%X7x
D_-e.h1?C7&r;~pn,KJPtb9[N`'
但是，y[1].append(8) 是往列表 y 的内嵌列表添加一个新元素，由于是浅拷贝，所以两个内嵌的列表是 x 和 y 共享的，该操作也会对列表 x 产生影响。

12.请问下面代码执行后，列表 s 的内容是什么？

>>> s = [1]
>>> s.append(s)

答：[1, [...]]。版权属于
<)o MT1I_tq5$ZO2,#'W(^9n@4;
解析:很多鱼油的答案应该是 [1, [1]]，但这是错误的。X+?WidZw=
ZFBd(XY<#+%2w;P*AT~p`ic'9h5b&?
首先，你得理解将变量与数据进行挂钩的这个行为，我们称之为引用：2tsv(B
Ez6&qCA[:ZXrG4QgK-Ulb
 

7"6t8iG|I*ZqH3Y>X:=!,oDWaF0$
那么，那么对于 s.append(s) 这样的代码，Python 会在列表的最后添加一个元素，并且其内容是指向 s，即自身：c3](F
sB*vf_0t$ah!4KWF.?i#V@CY
 

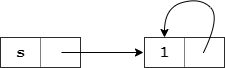
csUSn6G)z}0dFVvmQ[TE
那为什么结果是 [1, [...]] 呢？x:th

13.请使用列表推导式，创建一个内容为 [[0, 2], [1, 3], [2, 4], [3, 5], [4, 6], [5, 7]] 的列表？

>>> [[i - 1, i + 1] for i in range(1, 7)]
[[0, 2], [1, 3], [2, 4], [3, 5], [4, 6], [5, 7]]

14.请将下面的循环转换为列表推导式的形式实现？

>>> matrix = [[1, 2, 3],
...           [4, 5, 6],
...           [7, 8, 9]]
>>> diag = []
>>> for i in range(len(matrix)):
...     i *= matrix[i][i]
...     diag.append(i)
...
>>> diag
[0, 5, 18]

答案：

>>> diag = [i * matrix[i][i] for i in range(len(matrix))]
>>> diag
[0, 5, 18]

 15. 请问下面代码执行后，变量 x 和 y 的值分别是什么？

>>> x = "FishC"
>>> y = [x for x in "123"]

答：x 的值依旧是 'FishC'；y 的值是 ['1', '2', '3']。p*n$gu`'W
>(X}|W%T:9&krLI$vohZ'YfP!DECM
解析：列表推导式中，对 x 变量进行多次赋值，显然从“理论上“来说它的值应该被修改了才是。~: r9TxV
J{YI]<h0#y.H2N:@GF"ie5lm
但事实上并不会，这是由于它们处于不同作用域的原因——这个知识点我们在后面的课程中会有详细的讲解。

16.如何获取矩阵从右上角到左下角这条对角线上的元素？

>>> matrix = [[1, 2, 3],
...           [4, 5, 6],
...           [7, 8, 9]]

正解： 

>>> diag = [matrix[i][len(M)-1-i] for i in range(len(matrix))]
>>> diag
[3, 5, 7]

 17. 请使用列表推导式创建一个 4 * 5 的二维列表，并将每个元素初始化为数字 8。

>>> s = [[8] * 5 for i in range(4)]
>>> s
[[8, 8, 8, 8, 8], [8, 8, 8, 8, 8], [8, 8, 8, 8, 8], [8, 8, 8, 8, 8]]

18.请将下面 matrix 矩阵反向展开，即使得最终的结果为 [9, 8, 7, 6, 5, 4, 3, 2, 1]

>>> matrix = [[1, 2, 3],
...           [4, 5, 6],
...           [7, 8, 9]]

正解：

>>> flatten = [col for row in matrix for col in row][::-1]
>>> flatten
[9, 8, 7, 6, 5, 4, 3, 2, 1]

 

 

L动手题

1.给定一个整数列表 nums 和一个目标值 target，请在该数组中找出和为目标值的两个元素，并将它们的数组下标值打印出来。

比如给定的列表 nums = [2, 7, 11, 15]，目标值 target = 9，那么由于 nums[0] + nums[1] = 2 + 7 = 9，所以打印结果是：[0, 1]
 

nums = [2, 7, 11, 15]
target = 9

n = len(nums)
for i in range(n):
    for j in range(i+1, n):
        if nums[i] + nums[j] == target:
            print([i, j])

 这里两层嵌套循环的执行逻辑就是：外层循环获取一个被加数，然后和内层循环获取的每一个加数进行相加，判断它们的和是否等于 target 变量的值？如果是，则打印结果

2.这次我们想让用户自己来录入 nums 和 target 的数据……

nums = []

isInput = True
while isInput == True:
    x = input("请录入一个整数（输入STOP结束）：")
    if x != "STOP":
        nums.append(int(x))
    else:
        isInput = False

target = int(input("请录入目标整数："))

isFind = False
n = len(nums)
for i in range(n):
    for j in range(i+1, n):
        if nums[i] + nums[j] == target:
            print([i, j])
            isFind = True

if isFind == False:
    print("找不到！")

3.最后，回忆前面我们学习过的 random 模块，生成一个由 10000 个整数（范围是 1 ~ 65535）构成的随机列表，目标值 target 由用户输入。

import random

nums = []

for i in range(10000):
    x = random.randint(1, 65535)
    nums.append(x)

target = int(input("请录入目标整数："))

isFind = False
n = len(nums)
for i in range(n):
    for j in range(i+1, n):
        if nums[i] + nums[j] == target:
            print([i, j])
            isFind = True

if isFind == False:
    print("找不到！")

4. 请编写一个程序，判断给定的字符串 s 中括号的写法是否合法。

条件：
 

• 字符串仅包含 '('、')'、'['、']'、'{'、'}' 这三对括号的组合
• 左右括号必须成对编写，比如 "()" 是合法的，"(" 则是非法的
• 左右括号必须以正确的顺序闭合，比如 "{()}" 是合法的，"{(})" 则是非法的

s = input("请输入测试字符串：")

# 创建一个特殊列表
stack = []
    
for c in s:
    # 如果是左括号，那么添加到特殊列表中
    if c == '(' or c == '[' or c == '{':
        stack.append(c)
    # 如果是右括号的情况
    else:
        # 如果碰到右括号，但特殊列表中没有左括号，那么肯定是非法的
        if len(stack) == 0:
            print("非法T_T")
            break
    
        # 逐个给出 c 对应的右括号 d
        if c == ')':
            d = '('
        elif c == ']':
            d = '['
        elif c == '}':
            d = '{'
    
        # 对比 d 和从特殊列表尾部弹出的元素
        if d != stack.pop():
            print("非法T_T")
            break
else:
    # 如果循环走完，特殊列表不为空，那么肯定是左括号比右括号多的情况
    # 那肯定有同学会问：右括号比左括号多的情况在哪里判断？
    # 小甲鱼答：在上面 d != stack.pop() 的判断中已经可以排除了~
    if len(stack) == 0:
        print("合法^o^")
    else:
        print("非法T_T")

5. 如果有一个列表，其中占比超过一半的元素称之为主要元素，那么如何获取一个列表的主要元素呢？8i' &
@,G^".?OE&%QzBr6_(4uWj
题目给定的列表是：[2, 2, 4, 2, 3, 6, 2]&bZ2+Dz
nIJOdw;MeV^~@s$?C8GAf27cR>
请根据解题思路进行编程。Powered b
h|Tb_?H%J*Du[;g71]O"EWrc=C
解题思路：来自
Hv);^phi3w`(#%y:'0?xDWU7umjan
根据主要元素的定义，对列表进行排序操作之后，主要元素必然会出现在列表长度一半之后的一个位置上。cM`(I0:"V
N>vB?3zlfLU~t6FG&oI=w
所以，我们只需要判断列表中是否有超过一半的元素与中间元素相同即可（如果有，中间元素为主要元素；否则，不存在主要元素）。

​
nums = [2, 2, 4, 2, 3, 6, 2]
    
nums.sort()
length = len(nums)
half = nums[length // 2]
count = 0
    
for each in nums:
    if each == half:
        count += 1
if count > length / 2:
    print("存在主要元素，是：", half)
else:
    print("不存在主要元素！")

​

@!q#fY
A&6:9*uYFo+N#5,X<O(1dq|
E4"m9nTFB'D7rO8outvR<Q#
6. 其实上面这道题有一个经典的解法，就是使用摩尔投票法（Boyer–Moore majority vote）。`5XOv
iv"ycI!'K<}F2)-Ah &joSb
摩尔投票法有时候也被称为“多数投票法”，该算法解决的问题是如何在任意多的候选人中（选票无序），找到获得票数最多的那个。a07^V
JtSa{<PM 1(`nX6A]c57bCu)GY+okr
摩尔投票法分为两个阶段：来自：
~O3z%ZdT?${VIn]60bw7 iS'1v

• 对抗阶段：分属两个候选人的票数进行两两对抗抵消
• 计数阶段：计算对抗结果中最后留下的候选人票数是否有效

大家不妨可以将摩尔投票法的工作原理想象为诸侯争霸，假设每个国家都是全民皆兵，并且打起仗来都是以 1 换 1 的形式消耗人口，当一个国家人口总数为 0，那么 Gameover， 

nums = [2, 2, 4, 2, 3, 6, 2]
    
# 对抗阶段
major = nums[0]
count = 0
for each in nums:
    if count == 0:
        major = each
    if each == major:
        count += 1
    else:
        count -= 1
    
# 统计阶段
if nums.count(major) > len(nums) / 2:
    print("主要元素是：", major)
else:
    print("不存在主要元素。")

7.. 我们知道，列表的 index() 方法可以找到第一个匹配元素的下标，那么你有没有办法在不改变原列表的情况下，找到最后一个匹配元素的下标呢？（有两种方法可以实现）

第一种方法的思路是：通过拷贝获取一个列表的副本（题目要求不改变原列表），然后将该副本原地翻转，再通过 index() 方法获取翻转后指定元素的下标，最后，使用（列表的长度 - 1 - 翻转后的下标）得到最终的结果。

>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 8, 8, 5, 6, 3, 2, 1, 2]
>>> nums_copy = nums.copy()
>>> nums_copy.reverse()
>>> len(nums_copy) - 1 - nums_copy.index(1)
15

第二种解题思路，就是暴力搜寻法

>>> count = nums.count(1)
>>> length = len(nums)
>>> for each in range(length):
...     if nums[each] == 1:
...         count -= 1
...     if count == 0:
...         print(each)
...         break
...
15

8.请根据下面的内存关系图，分别创建出 x、y 和 z 三个不同的列表

x = [[0] * 3] * 3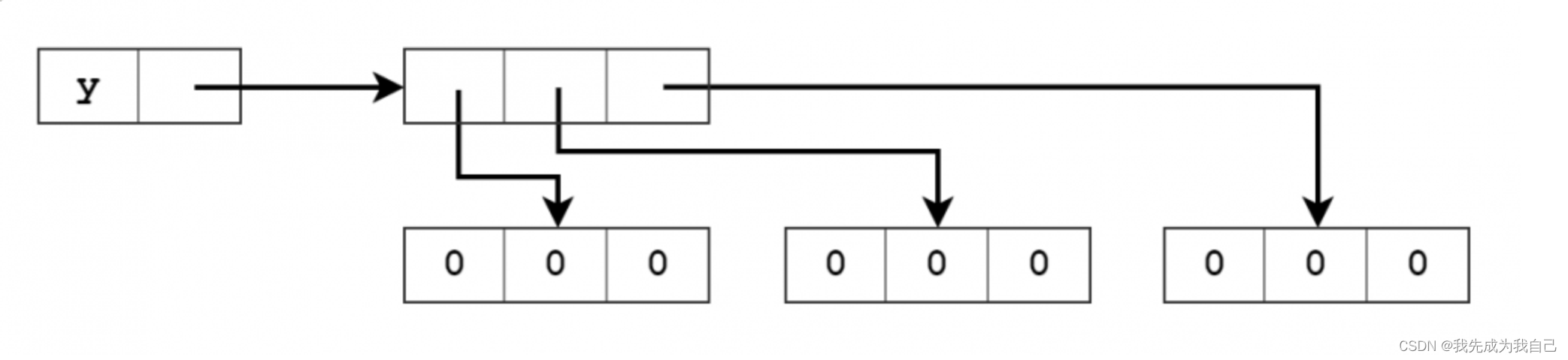

 

y = [0] * 3
for i in range(3):
    y[i] = [0] * 3

 

z = [0] * 3
for i in range(3):
    z[i] = [0] * 3
    for j in range(3):
        z[i][j] = [0] * 2

9.编写代码，利用“摩尔投票法”来找出占比数量最多的两个元素（注意：这两个元素的数量都需要超过总数的三分之一）

nums = [1, 1, 2, 1, 3, 2, 3, 2]
    
major1 = major2 = nums[0]
count1 = count2 = 0
    
# 对抗阶段
for each in nums:
    if major1 == each:
        count1 += 1
        continue
    
    if major2 == each:
        count2 += 1
        continue
    
    if count1 == 0:
        major1 = each
        count1 = 1
        continue
    
    if count2 == 0:
        major2 = each
        count2 = 1
        continue
    
    count1 -= 1
    count2 -= 1
    
# 统计阶段
if nums.count(major1) > len(nums) / 3:
    print(major1)
if nums.count(major2) > len(nums) / 3:
    print(major2)

10.创建一个88 x 88的随机整数矩阵（二维列表），然后匹配用户输入的整数是否与其中某元素相等，如果相等则打印其行号和列号 

要求1：随机整数取值范围 0~1024Powered b
MXahi0ok"d4f(qyB [.2l
要求2：需找出所有匹配的元素来自：
,LMQHO(`=.<nJmx l3k&$+*
程序实现演示：版权属于：
8,b@Q%BG?~Yy;ET4=-`nzFP
 

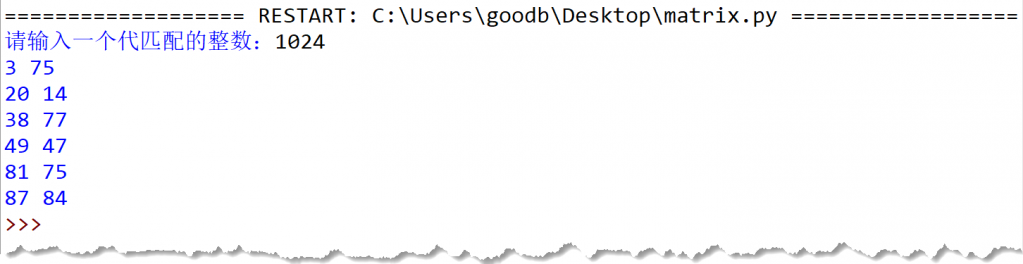
import random
    
# 创建并初始化二维列表
matrix = []
for i in range(88):
    matrix.append([])
    for j in range(88):
        matrix[i].append(random.randint(0, 1024))
    
target = int(input("请输入一个代匹配的整数："))
    
# 匹配用户输入的整数
for i in range(88):
    for j in range(88):
        if matrix[i][j] == target:
            print(i, j)

11.请编程找出矩阵中的幸运数字。

说明：假设给定一个 m * n 的矩阵（矩阵中数值的取值范围是 0~1024，且各不相同），如果某一个元素的值在同一行的所有元素中最小，并且在同一列的所有元素中最大，那么该元素便是幸运数字。
r~p>H' C4:03$W]xqNKag!{<ji
假设给定的矩阵如下：

matrix = [[10, 36, 52],
          [33, 24, 88],
          [66, 76, 99]]

那么输出结果应该是 66（同时满足同一行的所有元素中最小，并且在同一列的所有元素中最大）。

matrix = [[10, 36, 52],
          [33, 24, 88],
          [66, 76, 99]]
    
row = len(matrix)
col = len(matrix[0])
    
min_row = [1024] * row
max_col = [0] * col
    
# 遍历矩阵中的每一个元素
# 找到每行中最小的元素，并将它们存放到列表min_row中
# 找到每列中最大的元素，并将它们存放到列表max_col中
for i in range(row):
    for j in range(col):
        min_row[i] = matrix[i][j] if matrix[i][j] < min_row[i] else min_row[i]    # min(matrix[i][j], min_row[i])
        max_col[j] = matrix[i][j] if matrix[i][j] > max_col[j] else max_col[j]    # max(matrix[i][j], max_col[j])
    
# 遍历矩阵中的每一个元素
# 判断是否同时满足“同一行的所有元素中最小”和“同一列的所有元素中最大”
for i in range(row):
    for j in range(col):
        if matrix[i][j] == min_row[i] and matrix[i][j] == max_col[j]:
            print(matrix[i][j])

12.打印杨辉三角形Powered by https://fishc.com.cn
l&jwViqX_CN;<]hp7rAd~"Z=')3H
杨辉三角形是中国古代数学的杰出研究成果之一，是我国北宋数学家贾宪于 1050 年首先发现并使用的。而后南宋数学家杨辉在《详解九章算法》一书中记载并保存了“贾宪三角形“。因此，贾宪三角形又被称为杨辉三角形。?~z_&j@B
,B-2x(gpwv4C+_#[^8jIq@Pd
简单地说，杨辉三角形的构成如下面动图所示：4eE3U*TO@5
8Su`kg)'JR.>=X<m4c-*xf2T]br%

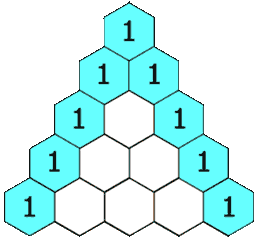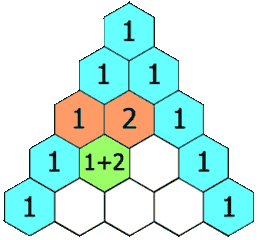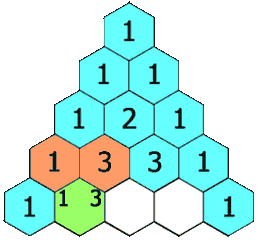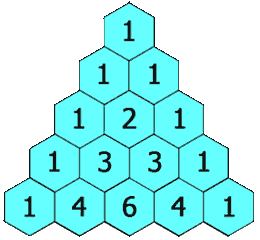
6$*v40U8(+1!)pEJBDt"9;%
从上面的动图我们可以得出一个道公式：杨辉三角形第i行j列的值 = 第 (i-1) 行 (j-1) 列的值 + 第 (i-1) 行 (j) 列的值8Ff[{:~174
kBvM !A[^b?P=|5DCd9*`SO<YmVo2
好，大家知道它的构成形式就可以开干了，千万不要以“我不懂数学，没听说过杨辉三角形”为理由放弃对本题目的挑战哦^o^b-${`XW;J
7aej|#~PFps3Jc]S-*r{'ul2A@_zLQ
好了，大家开拔吧！来自：https://fishc.com.cn
TD+`&~dO'Mwuh0U5= }#R@X.
编写代码，让程序实现如下：版权属于：https://fishc.com.cn
htK#,QXaP5p&=+<TNik]E;VScyfb

# 初始化杨辉三角形
# 创建一个10*10的二维列表，并将所有的元素初始化为0
triangle = []
for i in range(10):
    triangle.append([])
    for j in range(10):
        triangle[i].append(0)
    
# 计算杨辉三角形
# 根据观察，我们知道杨辉三角形左右两边的元素均为1
for i in range(10):
    triangle[i][0] = 1
    triangle[i][i] = 1
    
# 第i行j列的值 = 第(i-1)行(j-1)列的值 + 第(i-1)行(j)列的值
for i in range(2, 10):
    for j in range(1, i):
        triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]
    
# 输出杨辉三角形
for i in range(10):
    for j in range(i+1):
        print(triangle[i][j], end='  ')
    print()

+pjv4~kiV@>C,ah#A%!2qOg n("Dc
 

yJ:`Fcl*.!%UNtBLX{bd4,_)3Y
@$1_x?#&bM+i)-yEIw{;9(L.PV4
1. 在不使用超纲姿势的前提下，修改代码，将杨辉三角形按下图的形式打印：{kLN:
:hTl1pD([^vm'B;N fPOto*kr7)E

# 初始化杨辉三角形
# 创建一个10*10的二维列表，并将所有的元素初始化为0
triangle = []
for i in range(10):
    triangle.append([])
    for j in range(10):
        triangle[i].append(0)
    
# 计算杨辉三角形
# 根据观察，我们知道杨辉三角形左右两边的元素均为1
for i in range(10):
    triangle[i][0] = 1
    triangle[i][i] = 1
    
# 第i行j列的值 = 第(i-1)行(j-1)列的值 + 第(i-1)行(j)列的值
for i in range(2, 10):
    for j in range(1, i):
        triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]
    
# 输出杨辉三角形
for i in range(10):
    # 因为是三角形，所以i越小，前边需要填充的TAB越多
    for k in range((10-i)//2):
        print('\t', end='')
    for j in range(i+1):
        # 要形成“隔行错开”的效果，所以我们在偶数行加4个空格
        if i % 2 == 1:
            print("    ", end='')
        # 为何要使用TAB而非空格，大家可以将下面的end='\t'改成对应的空格数即可知晓
        print(triangle[i][j], end='\t')
    print()

14.

请使用列表推导式，获得 matrix 矩阵的转置矩阵 Tmatrix（将 matrix 的行列互换之后得到的矩阵，称为 matrix 的转置矩阵）。

>>> matrix = [[1, 2, 3, 4],
...           [5, 6, 7, 8],
...           [9, 10, 11, 12]]

什么是转置矩阵？来自：https://fishc.com.cn
~*MAXB5xO{3Yn<9g`kE%"^jwHVbfIP
一个矩阵 matrix，把它的第一行变成第一列，第二行变成第二列，……，最末一行变为最末一列，从而得到一个新的矩阵 Tmatrix。这一过程称为矩阵的转置。BE7>9l+
>A.@t9VTP$O?bGaN25<;,p
 

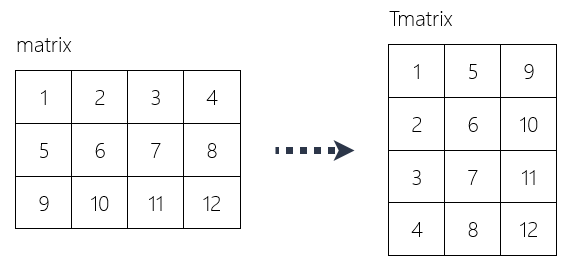
15.请按照顺时针螺旋顺序输出矩阵中的所有元素。EG FX9}i{'
M{lGB*ogv<+@}($A|eakb_ymUcsX6
比如矩阵 matrix 如下 

>>> matrix = [[1, 2, 3, 4],
...           [5, 6, 7, 8],
...           [9, 10, 11, 12]]

那么将输出：

[1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]

 

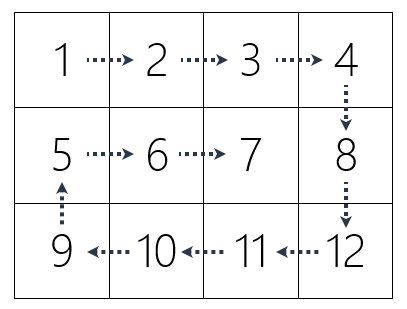
}=@isFYbD%,!WJpTkn XI^
提示1：根据已知矩阵，我们可以轻而易举地获取它四个方向的初始值（top: 0; right: 二维列表的“行”的长度; bottom: 二维列表的“列”的长度; left: 0）fz.jun
c,KrTV3zq;'g^pmuwP$v~|> (9Cy
 

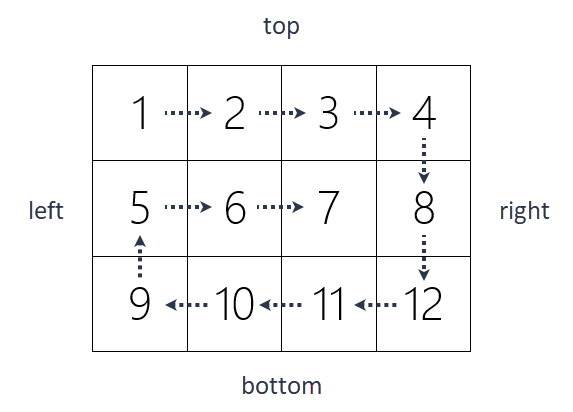
7GQxEuq~1<?3D6crbik=2
提示2：那么按照顺时针螺旋顺序……版权属于：https://fishc.com.cn
Bm>yE~"u3$tfhWdp_lJTki0beN

• 首先从左往右遍历，依次是 (top, left) 到 (top, right)
• 然后从上往下遍历，依次是 (top+1, right) 到 (bottom, right)
• 接着从右往左遍历，依次是 (bottom, right-1) 到 (bottom, left+1)
• 最后从下往上遍历，依次是 (bottom, left) 到 (top+1, left)

w3pWKSQ[56|:AMRPb1Ycy!n4q8%g
提示3：经过一轮的遍历，那么相当于走了外层一圈，接着应该怎么办？没错，应该进入下一层，也就是 left+1、right-1、top+1、bottom-1。wi5gZ6K
@xG9{F0n~qHJ<*P?5BZbCYOS
提示4：那么每前进一层 left 就加 1，right 就减 1，top 和 bottom 也是一样，那么无论这个二维列表有多大，都会遇到一个矛盾点，那就是 left 终究会大于 right，bop 终究会大于 bottom，对不对？所以嘛，这个就是结束的条件啦！]Qk,p{.