Transformer——Q70 GeLU激活函数 xΦ (x) 的近似误差分析（Φ 为CDF）-CSDN博客

本文链接：https://blog.csdn.net/pzccool/article/details/147843353

该问题归类到Transformer架构问题集——前馈网络——全连接层。请参考LLM数学推导——Transformer架构问题集。

1. 引言

在大语言模型（LLM）的复杂架构中，激活函数是赋予模型非线性表达能力的关键组件。GeLU（Gaussian Error Linear Units）激活函数凭借其独特的自适应特性，在 Transformer 等主流 LLM 架构中广泛应用。然而，由于其表达式 $GeLU(x)=x\Phi(x)$ 中的 $\Phi(x)$ （标准正态分布的累积分布函数）不存在显式初等函数形式，实际计算依赖近似方法，这就产生了近似误差问题。深入探究这些误差，对理解 LLM 的运行机制与性能优化至关重要。

2. GeLU 激活函数基础理论

2.1 函数定义与特性

GeLU 激活函数定义为 $GeLU(x)=x\Phi(x)$ ，其中 $\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{t^2}{2}}dt$ 。该函数通过融合输入 x 与标准正态分布的累积概率信息，实现自适应激活：当 x 较大时， $\Phi(x)$ 趋近于 1， $GeLU(x)$ 近似线性；当 x 较小时， $\Phi(x)$ 趋近于 0，对输入进行收缩。这种特性使 GeLU 能更好捕捉数据非线性特征，增强模型表达能力。

2.2 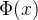$\Phi(x)$ 的常见近似方法

2.2.1 泰勒级数展开

基于泰勒级数在 x = 0 处展开 $\Phi(x)$ ，其展开式为 $\Phi(x)\approx\frac{1}{2}+\frac{1}{\sqrt{2\pi}}\sum_{n = 0}^{\infty}\frac{(-1)^n}{(2n + 1)n!2^n}x^{2n + 1}$ 。不过，远离 x = 0 时，需增加级数项数以保证精度，计算量也随之上升。

2.2.2 有理函数近似

通过构造 $R(x)=\frac{P(x)}{Q(x)}$ （P(x)、Q(x) 为多项式）逼近 $\Phi(x)$ ，常见形式如 $\Phi(x)\approx\frac{1}{2}\left(1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right)$ 。此方法在特定区间精度较好，计算效率较高。

2.2.3 查表法

预先计算存储一定范围内 x 对应的 $\Phi(x)$ 值，计算时查表获取近似值。该方法速度快，但精度受表格分辨率限制，插值计算会引入误差。

3. GeLU 激活函数近似误差分析

3.1 基于泰勒级数展开的误差

3.2 基于有理函数近似的误差

使用有理函数 $R(x)$ 近似 $\Phi(x)$ 得到 $GeLU_R(x)=xR(x)$ ，近似误差 $E_R(x)=|GeLU(x)-GeLU_R(x)|=|x(\Phi(x)-R(x))|$ 。其误差取决于有理函数形式与参数，优化后可在特定区间控制误差，但区间外误差可能增大。

3.3 基于查表法的误差

查表法得到 $\Phi_{table}(x)$ ，则 $GeLU_{table}(x)=x\Phi_{table}(x)$ ，近似误差 $E_{table}(x)=|GeLU(x)-GeLU_{table}(x)|=|x(\Phi(x)-\Phi_{table}(x))|$ 。误差主要源于表格分辨率，插值计算会导致结果与真实值存在偏差。

4. GeLU 激活函数在 LLM 中的使用分析

4.1 典型应用场景

4.1.1 文本生成任务

以 GPT 系列模型为例，在 Transformer 解码器的 FFN 中，GeLU 激活函数对自注意力机制输出特征进行非线性变换。如生成故事时，输入前文语义表征，GeLU 函数根据 “角色”“情节” 等语义特征分布，自适应调整激活程度。对关键情节特征增强激活，使生成内容逻辑连贯、情节精彩；对次要描述适度收缩，保证文本详略得当。

4.1.2 问答系统

在 BERT - QA 等问答模型中，GeLU 激活函数应用于 Transformer 编码器。当用户提问 “爱因斯坦的主要贡献有哪些？” ，模型编码问题与答案文本时，GeLU 函数对 “爱因斯坦”“贡献” 等关键语义特征相关向量增强激活，突出关键信息。经过多层编码处理，模型准确理解问题，从文本中提取 “相对论”“质能方程” 等答案。

4.1.3 语言翻译

在 Transformer 神经机器翻译模型中，GeLU 激活函数贯穿源语言编码与目标语言解码过程。如中译英时，源语言句子编码阶段，GeLU 函数依据中文语义和语法特征调整向量特征，助力模型理解句子结构；目标语言解码生成英文时，根据已生成内容和源语言语义，进一步优化特征，生成符合英文表达习惯的译文。

4.2 近似误差的影响

4.2.1 对模型训练的影响

在训练情感分析模型时，若 GeLU 激活函数近似误差导致文本特征表示不准确，模型可能将积极情感误判为消极。例如把 “这部电影太棒了” 错误分类，影响训练准确率，导致训练不稳定、收敛缓慢，甚至无法收敛到最优解。

4.2.2 对模型推理的影响

在医疗诊断辅助 LLM 中，医生输入患者症状描述，若 GeLU 近似误差使模型误解关键症状信息，可能给出错误诊断建议，延误病情。在金融风险评估场景，误差可能导致模型对金融文本风险判断偏差，给投资者带来经济损失。

5. 优缺点分析

5.1 优点

自适应能力强：能依据数据分布动态调整激活，更好捕捉语义特征，提升 LLM 对复杂语言模式的学习能力。
理论基础扎实：基于标准正态分布，为模型理论分析和优化提供支撑。
性能表现出色：在多项 LLM 任务中，相比部分激活函数，收敛更快，处理长序列数据效果好，泛化能力强。

5.2 缺点

计算复杂度高：因 $\Phi(x)$ 需近似计算，增加计算量，影响训练和推理效率。
误差影响显著：近似误差导致训练不稳定、推理结果不准确，高精度场景下问题突出，增加模型调试难度。
可解释性不足：工作机制复杂，缺乏直观解释，不利于分析模型行为和优化。

6. 优化策略

6.1 改进近似方法

针对泰勒级数展开，优化余项估计，根据 x 范围和精度动态确定项数；对有理函数近似，采用遗传算法等智能算法优化参数，提升不同区间近似精度。

6.2 混合近似策略

结合多种近似方法，如 |x| 较小时用泰勒级数展开，较大时切换有理函数近似；或先查表获取初值，再用其他方法修正，平衡计算速度与精度。

6.3 硬件与架构优化

利用 GPU 并行计算加速近似计算；采用分布式计算框架处理大规模训练任务。同时优化 LLM 架构，增加深度和宽度提升鲁棒性，引入误差补偿机制降低误差影响。

7. 代码示例

import torch
import math

def taylor_approx_phi(x, n):
    """
    使用泰勒级数展开近似标准正态分布的累积分布函数 \(\Phi(x)\)
    :param x: 输入值
    :param n: 泰勒级数展开的项数
    :return: \(\Phi(x)\) 的近似值
    """
    sum_terms = 0
    for i in range(n):
        term = ((-1) ** i / ((2 * i + 1) * math.factorial(i) * (2 ** i))) * (x ** (2 * i + 1))
        sum_terms += term
    return 0.5 + (1 / math.sqrt(2 * math.pi)) * sum_terms

def taylor_approx_gelu(x, n):
    """
    使用泰勒级数展开近似GeLU激活函数
    :param x: 输入值
    :param n: 泰勒级数展开的项数
    :return: GeLU(x) 的近似值
    """
    phi_approx = taylor_approx_phi(x, n)
    return x * phi_approx

# 示例调用
x = torch.tensor(1.0)
n_terms = 5
approx_value = taylor_approx_gelu(x, n_terms)
print(approx_value)

8. 代码解读

上述代码通过两个自定义函数实现基于泰勒级数展开的 GeLU 激活函数近似。taylor_approx_phi函数根据泰勒级数公式计算标准正态分布累积分布函数 $\Phi(x)$ 的近似值，taylor_approx_gelu函数调用前者结果，结合 GeLU 激活函数定义完成最终近似计算。示例调用部分设定输入值x和展开项数n_terms，展示函数实际使用方式并输出近似结果。

9. 总结

通过对 GeLU 激活函数 $x\Phi(x)$ 近似误差的深度解析，我们全面了解了其理论基础、近似方法、在 LLM 中的应用及误差影响。尽管 GeLU 在 LLM 中优势显著，但近似误差带来的挑战不容忽视。通过优化近似方法、采用混合策略和改进模型架构等手段，可有效降低误差影响。未来，随着 LLM 不断发展，对激活函数近似误差的研究将持续推动自然语言处理技术进步。