NOIP 2013 - 提高组 火柴排队 归并排序+逆序对 重庆一中高2018级竞赛班第六次测试 2016.7.31 Problem 4

【问题描述】
涵涵有两盒火柴，每盒装有 n 根火柴，每根火柴都有一个高度。现在将每盒中的火柴各自排成一列，同一列火柴的高度互不相同，两列火柴之间的距离定义为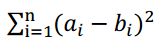：，其中 ai表示第一列火柴中第 i 个火柴的高度，bi表示第二列火柴中第 i 个火柴的高度。

每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 99,999,997 取模的结果。

【输入格式】
共三行，第一行包含一个整数 n，表示每盒中火柴的数目。
第二行有 n 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。
第三行有 n 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。

【输出格式】
输出共一行，包含一个整数，表示最少交换次数对 99,999,997 取模的结果。

【输入样例】
【样例1】

4 
2 3 1 4 
3 2 1 4

【样例2】

4 
1 3 4 2 
1 7 2 4

【输出样例】
【样例1】

1

【样例2】

2

【样例解释】
【样例1说明】
最小距离是 0，最少需要交换 1 次，比如：交换第 1 列的前 2 根火柴或者交换第 2 列的前 2 根火柴。
【样例2说明】
最小距离是 10，最少需要交换 2 次，比如：交换第 1 列的中间 2 根火柴的位置，再交换第 2 列中后 2 根火柴的位置。

【数据范围】
对于 10%的数据， 1 ≤ n ≤ 10；
对于 30%的数据，1 ≤ n ≤ 100；
对于 60%的数据，1 ≤ n ≤ 1,000；
对于 100%的数据，1 ≤ n ≤ 100,000，0 ≤火柴高度≤ 2^31 - 1。

思路：完全想不到用逆序对来做，考试的时候还以为是某种贪心算法。（2016.8.3：昨天晚上想了一下觉得这道题应该也含有贪心思想，要将两个队列都由小到大排序。）
正解是：将A,B两个队列都从小到大排序，排序后A队列第i个位置的火柴原来的id就是现在B队列第i个位置的火柴应该交换到的位置，在将B队列还原，理由为数论中的排序不等式（根本不知道是什么鬼，请自行谷歌）。

/*
    Name: match.cpp
    Copyright: Twitter & Instagram @stevebieberjr
    Author: @stevebieberjr
    Date: 02/08/16 19:33
*/
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 100005
#define mod 99999997
using namespace std;

int n;

struct data
{
    int s,id,d;
}m1[maxn],m2[maxn];

bool cmp1(data a,data b)
{
    return a.s<b.s;
}

bool cmp2(data a,data b)
{
    return a.id<b.id;
}

int t[maxn];

long long calc(int x,int y)
{
    if(x>=y) return 0;
    int m=(x+y)>>1;
    long long t1=calc(x,m);
    long long t2=calc(m+1,y);
    long long t3=0;
    int i=x,j=m+1,k=x;
    for(;i<=m && j<=y;)
    {
        if(m2[i].d>m2[j].d)
        {
            t[k++]=m2[j++].d;
            t3+=(m-i+1)%mod;
        }
        else t[k++]=m2[i++].d;
    }
    for(;i<=m;) t[k++]=m2[i++].d;
    for(;j<=y;) t[k++]=m2[j++].d;

    for(int i=x;i<=y;i++) m2[i].d=t[i];

    return ((t1+t2)%mod+t3)%mod;
}

int main()
{
    freopen("match.in","r",stdin);
    freopen("match.out","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&m1[i].s);
        m1[i].id=i;
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&m2[i].s);
        m2[i].id=i;
    }
    sort(m1+1,m1+1+n,cmp1);
    sort(m2+1,m2+1+n,cmp1);
    for(int i=1;i<=n;i++)
    {
        m2[i].d=m1[i].id;
    }
    sort(m2+1,m2+1+n,cmp2);
    long long ans=calc(1,n);
    cout<<ans<<endl;
    return 0;
}