三大核心运算

一、函数求极限

1. 无穷小的比较

1. =0，∞，k，0

2. 常见的等价无穷小

   1. 一阶，二阶，三阶

3. 等价替换原理
   注意：整个极限而言 ==乘除因子==中才可以用替换，加减用泰勒或者化简变成乘替换！

4. 等价无穷小的充要条件
   化成 ‘=’ 号,加上误差
   
   

2.泰勒公式

3.极限运算法则

1. 极限的加减乘除

2. 抓大头

3. 复合函数
   注意：里面的极限是趋向而不能相等

4. 洛必达法则
   
   

4. 求极限通法

1. 代入x，分析极限类型和可使用的化简
2. 化简：
   多考虑，抓大头，+1-1，开根号等
3. 求值
   1. 洛必达和泰勒
      

5. 典型例题和补充细节

重点在化简部分：

1. 去根号：n-n 化成 n+n直接得出结果，注意 | x^2| = ±x
2. 提公因式：有e什么 - e什么的就提前方便的再重要极限

二、函数求导

1. 定义

1. 变化率

注意：一般都是考一个点的导数，就先写定义上去，一个个找就行

2. 几何意义
   1. 斜率，切线，法线

总结：
计算：一般都用到洛必达法则，因为要得出导数

2. 各类型函数求导

1. 基本求导公式和四则运算
2. 复合函数求导
3. 隐函数求导（直接求）
4. 参数方程求导
5. 反函数求导
6. 高阶导数
   1. 找规律
   2. 莱布尼茨公式
   3. 泰勒公式
      
      
      
      

三、积分

01、不定积分

1. 概念与基本公式.

1. 概念
2. 基本积分公式
   

2. 四大积分方法

1. 第一类换元法（微分法）

2. 第二类（去根号）
   1. 一次
   2. 二次

技巧注意

1.二次三角换元时，注意什么时候用反函数，什么时候用画图直接搞数

3. 分部积分法

在，想不到或用不了（1）时，先用试试；
或者多做题了解清楚大概什么题型可以用。（如：分母是2次方等等）

4. 有理函数积分法
   
   

3. 三角有理函数积分

技巧

1.凑的技术：搞不定时可以试着凑（分子和分母的关系）【如，1/2(a-b+b+a)就是几组的组合了，看有没有分子和分母有积分导数联系的等等 】
2.分子为常数时，可以处或者乘些东西，让其有操作性（如：常见secx^2 = dtanx,tanxsec = d secx 等等）
3.+1-1，和弄平方差

∫cscx dx
=∫1/sinx dx
=∫1/[2sin(x/2)cos(x/2)] dx,两倍角公式
=∫1/[sin(x/2)cos(x/2)] d(x/2)
=∫1/tan(x/2)*sec²(x/2) d(x/2)
=∫1/tan(x/2) d[tan(x/2)],注∫sec²(x/2)d(x/2)=tan(x/2)+C
=ln|tan(x/2)|+C。

02 定积分

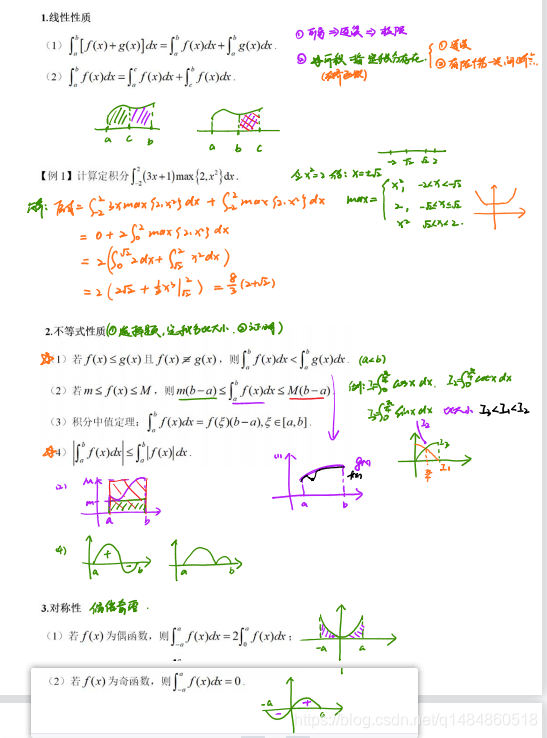
1. 性质

1. 线性性质
2. 不等式性质
3. 对称性
   

2. 计算

1. 牛顿莱布尼茨公式
2. 定积分的换元法
3. 分部积分
4. 区间再现
5. 华里士公式

03变限积分与反常积分

1. 变限积分

1. 形式
2. 连续性
3. 可导性
4. 变限积分的导数
   
   
   
   

2. 反常积分

1. 无穷限上的反常积分
2. 无界函数
3. 伽玛函数