4 矩阵分析
4.1 向量范数
1.概念
向量x属于空间V,若有一种实值函数f(x)能将向量x映射为一个实数,记作f(x)=||x||,只要这个实值函数||x||满足
1)正定性: ||x|| ≥ 0
2)齐次性: ||kx|| = |k|||x||(
k∈N
)
3)三角不等式: ||x+y|| ≤ ||x||+||y|| ( x,y均为V空间的向量)
那么这个函数||x||就可以用来表征向量x的大小,叫做向量x的范数。凡是满足这三个条件的的实值函数都能当做向量范数。这个有了范数的空间V也叫做赋范线性空间。
2.常用的向量范数
p-范数
向量
x=(x1,x2,...xn)
, 定义向量x的p-范数为
| 常用的向量范数 | 求法 |
|---|---|
| ||x||1 | 向量中所有元素的模的和 |
| ||x||2 | 向量中所有元素的模的平方和,再求和的平方根 |
| ||x||p | 向量中所有元素的模的p次幂的和,再对和开p次方 |
| ||x||∞ | 向量中所有元素的模的最大值 |
4.2 矩阵范数
1.概念
定于矩阵A的一个实函数,记作f(A)=||A||,只要这个函数||A||满足
1)正定性: || A || ≥ 0
2)齐次性: ||k A || = |k||| A ||
3)三角不等式: || A +B|| ≤ || A ||+||B||
4) 相容性: ||AB|| ≤ ||A||||B|| (乘积不等式)
此时称||A||是矩阵A的范数,如果只满足前3个条件,那只是广义矩阵范数。
2.几种常见的矩阵范数
| 常用的矩阵范数 | 名称 | 求法 |
|---|---|---|
| ||A||1 | 列和范数/列范数 | 对每一列求各个元素的模的和,有n列就有n个和,再取这些和的最大值 |
| ||A||∞ | 行和范数/行范数 | 对每一行求各个元素的模的和,有n行就有n个和,再后取这些和的最大值 |
| ||A||2 | 谱范数 | AHA 的所有特征值中的最大值的平方根 |
4.3 特征值估计
1.盖尔圆
方阵的盖尔圆所在的平面为复平面,x轴为实数,y轴为虚数,方阵的特征值只会出现在盖尔圆内。N阶方阵
A(aij)
共有n个盖尔圆,它的第i个盖尔圆以
aii
为圆心,以
为半径,即第i个盖尔圆的半径以矩阵第i行,除去对角元素的,其他所有元素的模的和。
第i个盖尔圆 Gi 的表示为
有k个孤立的盖尔圆内则至少有k个相异的特征值,相交的盖尔圆内可能有重根。
4.4 矩阵函数
1.概念
矩阵函数
如果矩阵A中的每个元素 aij(t) 都是变量t的函数,则称A(t)为矩阵函数。如果矩阵的每个元素都有极限,则这个矩阵函数也有极限。矩阵序列
矩阵序列 A(k)m×n,k∈N , 共有 m×n 个元素,那么就有 m×n 组数列, 当每个数列 {aij(k)} 均分别收敛于相应的极限 aij 时,则矩阵序列{A(t)}收敛于A, 其中A由 aij 组成。谱半径
矩阵A所有特征值的模的最大值单纯矩阵与矩阵函数
对于可对角化的单纯矩阵而言,f(A)的特征值就是f(λ),可用来求f(A)的谱分解和谱半径
2.判断矩阵幂级数敛散性
1)考虑矩阵幂级数
∑A(k)
, 先把矩阵A换成未知数x,计算这个数项幂级数
∑x(k)
的收敛半径R
2)求矩阵A的特征值,并计算其谱半径
ρ(λ)
(特征值模的最大值)
3)若
ρ(λ)<R
,则矩阵幂级数绝对收敛;
若
ρ(λ)>R
,则发散
4)若
ρ(λ)=R
,上述方法失效,可计算A(k)的Jordan形,
A(n)=P−1J(k)P
,通过证明J(k)的敛散来证明A(k)的敛散,进而证明
∑A(k)
的敛散。
5) J(k)的每个元素都是关于n的级数,看看当n->∞时,所有元素是不是都收敛,有一个不收敛就是发散,都收敛时,A的矩阵幂级数才收敛
3.矩阵函数的计算方法
- Jordan标准型法(不推荐)
1)求m阶矩阵A的Jordan标准形J和可逆阵P, P−1 ,使得 P−1AP=J
2)求f(J), f(J)=diag(f(J1),f(J2),…f(Jm)) ,其中 f(Ji)r×r
3) f(A)=Pf(J)P−1
- 待定系数法(推荐)
1)求A的最小式,得到最小次的总次数degmA(λ)=k
2)令 p(λ)=b0+b1λ+b2λ2+…+bk−1λk−1 , k是几就有几个b, b0…bk−1
3)列方程组
p(λi)=f(λi)
若 λi 是2重根,则再设 p′(λi)=f′(λi)
如f(A)=sinA, mA(λ)=(λ−2)2(λ−1) ,令 p(λ)=b0+b1λ+b2λ2 ,要满足的方程组为
⎧⎩⎨⎪⎪P(1)=sin1P(2)=sin2P′(2)=cos2
即
⎧⎩⎨⎪⎪b0+b1+b2=sin1b0+2b1+4b2=sin2b1+4b2=cos2
4)解出
bi
,即解出了p(λ), 把p(λ)换成A就是p(A), 最后f (A)= p(A)
4.4 矩阵求导
矩阵求导包括标量,行向量 xT , 列向量x,矩阵之间的求导。
1. 矩阵Y=F(x)对标量x求导
相当于矩阵
Ym×n
中的每个元素对x求导,转化为
m×n
次普通的求导
2. 标量y对列向量x求导
相当于标量y对列向量x的每个分量求偏导,再组成一个新的列向量
3. 行向量 yT 对列向量x求导
相当于行向量
yT
的每一个分量作为标量对列向量x求导,转化为标量对列向量x求导的情况。考虑
yT=(y1,y2,…yn)T,x=(x1,x2,…,xm)
,则y的n个分量都对x的求导,得到n个维度为m的列向量,最后这n个列向量再组成m行n列的矩阵。
注意:
1.
1×n
的行向量对
m×1
的列向量求导后是
m×n
的矩阵。
2. 重要结论:
4. 列向量y对行向量 xT 求导
转化为行向量
yT
对列向量 x 的导数,然后转置。
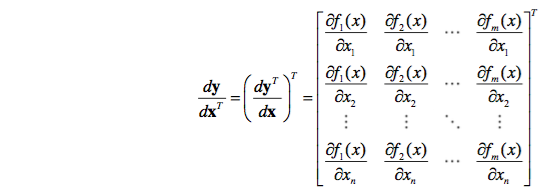
注意
1. m×1 向量对 1×n 向量求导结果为 m×n 矩阵。
2. 重要结论:
5. 向量积 uTv 对列向量x求导的运算法则
例如:
6. 矩阵Y对列向量x求导
将Y对x的每一个分量求偏导,构成一个超列向量,超向量中的每个分量都是一个矩阵。转化为矩阵对标量求导的情况。
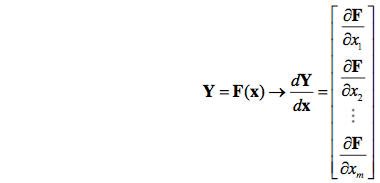
注意:矩阵对列向量求导的结果是以矩阵作为分量的超向量。
7. 矩阵Y对行向量 xT 求导
相当于Y对
xT
的每一个分量求偏导,结果是个超级行向量。
8.标量y对矩阵X求导
相当于标量y对矩阵X中的每个元素求导,结果是个和矩阵X行列相等的矩阵
重要结论:
9. 矩阵Y对矩阵X求导
将矩阵
Ym×n
的每个元素对矩阵X求导,转化为
m×n
个标量对矩阵
Xs×r
求导,最后排起来得到
m×n
的超级矩阵,其中每个元素为
s×r
的矩阵。
矩阵对矩阵求导的结果是以矩阵作为元素的超级矩阵。












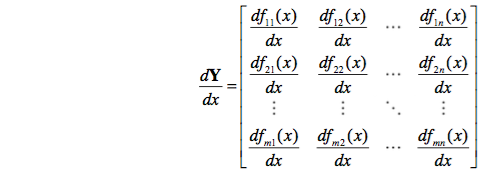
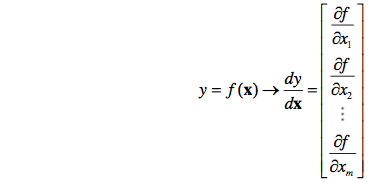
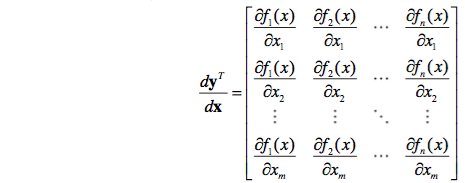
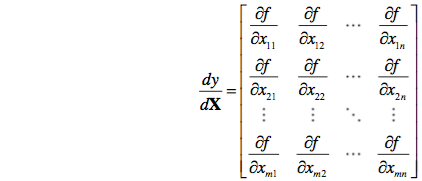

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








