线性回归方法(1)

线性模型使用范围

相比于非线性模型，线性模型更适用于：
1. 小数据集
2. 低信噪比
3. 稀疏数据

1. 线性回归模型

约定数据集$X=(X_1,X_2,...,X_p)$有p个特征，$X_j \in R^N$共N个样本。

$$f(X)=\beta_0+\sum_{i=1}^p X_j\beta_j$$

给X增加一列1，$X=(1, X_1,X_2,...,X_p)$， $\beta=(\beta_0, \beta_1, ..., \beta_p)^T$，上式可写成矩阵形式：

$$f(X)=X\beta$$

这里的$f(X)$为真实模型，$\beta$为真实模型参数，相对应的有估计模型和估计参数, 估计模型的结果为估计的响应变量y

$$\hat{y}=\hat{f}(X)=X\hat{\beta}$$

在统计学习里，我们一般认为真实的,即观测到的响应变量为估计与误差的叠加

$$y=\hat f(X)+\varepsilon=X \hat \beta+\varepsilon$$

这里$\varepsilon=(\varepsilon_0, \varepsilon_1,...,\varepsilon_N)^T$, 是每个样本预测值和真实值的误差组成的向量，假设它服从高斯分布

$$\varepsilon \sim N(0, \sigma^2I_N )$$

那么y也服从高斯分布

$$y \sim N(X\beta, \sigma^2I_N )$$

根据X的不同来源，线性模型的表达能力可以得到极大的扩展：

• 定量输入
• 定量输入的变换，如log, 平方根，平方
• 基展开，如$X_2=X_1^2, X_3=X_1^3$
• 哑变量，类别变量做独热编码变成的由0，1组成的稀疏矩阵
• 交互项，如$X_3=X_1X_2$

2. 最小二乘法

2.1 求解方法与理解

为了求得真实模型，我们希望y和$\hat{y}=X\hat \beta$的误差尽量小，因此需要求得使残差平方和$RSS(\beta)=(y-X\beta)^T(y-X\beta)$最小的模型参数$\beta$，这是无约束二次优化问题，直接求导即可

$$\frac{\partial RSS(\beta)}{\partial \beta}=-2X^T(y-X\beta)=0$$

$$X^TX\beta = X^Ty$$

当X列满秩时，若以y为未知数，方程组Xy=0中y只有0解，而这里y≠0，因此Xy≠0，所以$y^T(X^TX)y=(Xy)^T(Xy)>0$，即$X^TX$正定，非奇异，则

$$\hat{\beta} = (X^TX)^{-1}X^Ty$$

其实，要使所求解为极小值点也必须满足

$$\frac{\partial ^2RSS(\beta)}{\partial \beta \partial \beta^T}=2X^TX>0$$

因此X列满秩是必须满足的条件。下面只讨论X列满秩的情况。
那么

$$\hat{y} =X\hat{\beta}$$

可见，$\hat{y}$是X列向量的线性组合，$\hat{y} \in span<X_0, X_1,...,X_p>$，所以

$$dim(\hat y)=p+1$$

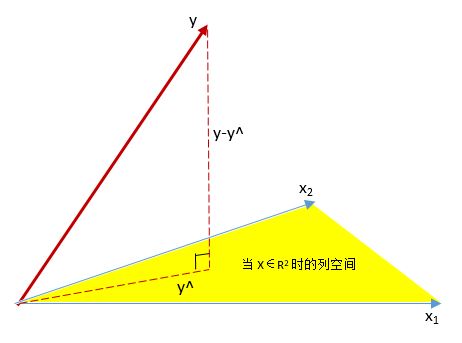
真实的$y=f(X)+\varepsilon$, 由于误差的存在，y不在X的列空间里边。所以，对于最小二乘法来说，最小化残差平方和$min||y-\hat{y}||^2$即找到一个$\hat y$使得$y-\hat y$正交于X的列空间。此时，$||y-\hat{y}||$取得最小值，放张图感受一下。

根据维数公式，有

$$\begin{eqnarray}dim(y) &=&dim(\hat y) + dim(y-\hat y)-dim(\hat y\bigcap (y-\hat y))\\ &=&dim(\hat y) + dim(y-\hat y)\\ \end{eqnarray}$$

所以，$dim(y-\hat y) = dim(y)-dim(\hat y) = N-(p+1)$(求这个是为了后面求卡方分布的自由度)
那么，什么是回归？就是求y在X列空间的投影，所以我们说$\hat{y}$是y在X上的回归。而最小二乘法所做的就是找到这种正交映射。令$H=X(X^TX)^{-1}X^T$

$$\hat{y} =X\hat{\beta}=X(X^TX)^{-1}X^Ty=Hy$$

H就是这个投影矩阵。

2.2 $\hat \beta$的期望与方差

我们估计的$\hat{\beta}$与真实的$\beta$差别有多大呢？

$$\begin{eqnarray}E_{Y|X}(\hat{\beta}) &=&E_{Y|X}((X^TX)^{-1}X^Ty)\\ &=&(X^TX)^{-1}X^TE_{Y|X}(y)\\ &=&(X^TX)^{-1}X^TX\beta\\ &=&\beta \end{eqnarray}$$

可见，用最小二乘法所估计出来的模型参数是无偏估计。

$$\begin{eqnarray}Var_{Y|X}(\hat \beta) &=&E_{Y|X}[(\hat{\beta}-E_{Y|X}(\hat{\beta}))(\hat{\beta}-E_{Y|X}(\hat{\beta}))^T]\\ &=&E_{Y|X}[((X^TX)^{-1}X^T\varepsilon)((X^TX)^{-1}X^T\varepsilon)^T]\\ &=&E_{Y|X}[(X^TX)^{-1}X^T\varepsilon \varepsilon^TX(X^TX)^{-1}]\\ &=&(X^TX)^{-1}X^TE_{Y|X}(\varepsilon \varepsilon^T)X(X^TX)^{-1}\\ &=&(X^TX)^{-1}X^TX(X^TX)^{-1}E(\varepsilon \varepsilon^T)\\ &=&(X^TX)^{-1}E(\varepsilon \varepsilon^T)\\ &=&(X^TX)^{-1}[E(\varepsilon \varepsilon^T)-0]\\ &=&(X^TX)^{-1}[E(\varepsilon \varepsilon^T)-E^2(\varepsilon)]\\ &=&(X^TX)^{-1}Var(\varepsilon)\\ &=&(X^TX)^{-1}\sigma^2I_N\\ \end{eqnarray}$$

其中

$$\begin{eqnarray}\hat{\beta}-E_{Y|X}(\hat{\beta}) &=&(X^TX)^{-1}X^Ty-\beta\\ &=&(X^TX)^{-1}X^Ty-(X^TX)^{-1}X^TX\beta\\ &=&(X^TX)^{-1}X^T(y-X\beta)\\ &=&(X^TX)^{-1}X^T\varepsilon\\ \end{eqnarray}$$

另外，如果我们能估计出$\sigma$，那么也就能估计出$Var(\hat \beta)$, 也就能求出$\hat \beta$的置信区间了。
我们知道，误差服从高斯分布

$$y-\hat y \sim N(0, \sigma^2I_N)$$

$$\frac{y-\hat y}{\sigma} \sim N(0, I_N)$$

$$\frac{||y-\hat y||^2}{\sigma^2} \sim \chi^2_{dim(y-\hat y)}=\chi^2_{N-p-1}$$

$$||y-\hat y||^2 \sim \sigma^2 \chi^2_{N-p-1}$$
残差平方和服从自由度为N-p-1的卡方分布(一个高斯分布的平方自然是 $\chi ^ 2$分布了)，所以有
$$E||y-\hat y||^2 = (N-p-1)\sigma^2$$

则

$$\sigma^2 = \frac{1}{N-p-1}E||y-\hat y||^2$$

$$\hat \sigma^2 = \frac{1}{N-p-1}\sum_{i=1}^N(y_i-\hat y_i)^2$$

可证明，上面的$\hat \sigma$是$\sigma$的无偏估计。因此

$$E(\hat \beta)=\beta$$

$$Var(\hat \beta)=(X^TX)^{-1}\hat \sigma^2I_N$$

2.3 $\hat \beta_j$的假设检验

2.3.1 单个$\hat \beta_j$的假设检验

由$\hat{\beta} = (X^TX)^{-1}X^Ty$，以及y服从高斯分布可知，$\hat{\beta}$也服从高斯分布

$$\hat{\beta} \sim N(\beta, (X^TX)^{-1}\hat \sigma^2I_N)$$

写成分量形式，对于 j=1,2,…,N,

$$\hat{\beta_j} \sim N(\beta_j, v_{jj} \hat \sigma^2)$$

其中，$v_{jj}$为$(X^TX)^{-1}$的第j个对角元，$v_{jj} \hat \sigma^2$是$\hat{\beta_j}$的方差，其标准差应为$\sqrt{v_{jj}} \hat \sigma$。不过，我们不知道是否有$v_{jj} > 0$

设$u \in R^{p+1}$列向量，构造$w=(X^TX)^{-1}u$，也是p+1维列向量，自然有$u=X^TXw$，因此

$$\begin{eqnarray}u^T(X^TX)^{-1}u &=&(X^TXw)^T(X^TX)^{-1}X^TXw \\ &=&w^TX^TX(X^TX)^{-1}X^TXw \\ &=&w^TX^TXw \\ &=&(Xw)^T(Xw) \geq0 \end{eqnarray}$$

显然，只有当u=0时，才有w=0,进而才恒有$u^T(X^TX)^{-1}u=0$, 因此$(X^TX)^{-1}$正定，故$v_{jj}>0$，此时我们可以写出参数$\hat \beta_j$的z分数了。

$$z=\frac{\hat \beta_j}{std(\hat \beta_j)}=\frac{\hat \beta_j}{ \sqrt{v_{jj}}\hat \sigma} \sim t_{N-p-1}$$

在原假设$\hat \beta_j=0$下，z服从自由度为N-p-1的t分布(一个高斯分布除以一个$\chi ^ 2$分布的平方根，自然是t分布了)，绝对值大的z分数，其对应的p值(可以查t分布表)也就越小，越可以拒绝原假设，即$\hat \beta_j>0$，相应的特征$X_j$应该被保留。
当N足够大时，t分布近似于高斯分布，t分布的尾分数与高斯分布的尾分数几乎相等，因此也可认为z服从高斯分布。这是一般的假设检验过程，这里不详述了。

2.3.2 多个$\hat \beta_j$的假设检验

F统计量可检验一组系数是否可置0,

$$F=\frac{(RSS_0-RSS_1)/(p_1-p_0)}{RSS_1/(N-p_1-1)}$$

其中$RSS_1$是用较大模型(参数多)算出来的残差平方和，$p_1$是该模型的参数数量(特征维数)，$RSS_0$是较小模型的残差平方和，$p_0$是该模型的参数数量(特征维数)。在高斯假设下，设较小模型更正确为零假设下，F统计量服从$F_{p_1-p_0, N-p_1-1}$分布，可查表得到相应p值以判断是否拒绝原假设，即较小模型是否更好。

2.4 $\hat \beta_j$的置信区间

上面提到参数$\hat \beta_j$的z分数

$$z=\frac{\hat \beta_j}{ \sqrt{v_{jj}\hat \sigma^2}} \sim t_{N-p-1}$$

z服从自由度为N-p-1的t分布，那么z的$1-\alpha$置信区间为

$$(-z^{1-{\alpha \over 2}}, z^{1-{\alpha \over 2}})$$

因此真实模型参数$\beta_j$的$1-\alpha$置信区间为

$$(\hat \beta_j-z^{1-{\alpha \over 2}}v_{jj}^{1 \over 2}\hat \sigma, \hat \beta_j+z^{1-{\alpha \over 2}}v_{jj}^{1 \over 2}\hat \sigma)$$

其中$z^{1-{\alpha \over 2}}$可通过查表得到。比如我想要个95%置信区间

$$\alpha=1-0.95=0.05$$

$$1-{\alpha \over 2}=1-0.025=0.975$$

若样本较多，N很大，可查标准正太分布表有

$$z^{1-{\alpha \over 2}}=z^{0.975}=1.96$$

所以$\beta_j$的95%置信区间为

$$(\hat \beta_j-1.96v_{jj}^{1 \over 2}\hat \sigma, \hat \beta_j+1.96v_{jj}^{1 \over 2}\hat \sigma)$$

---

总结自The Elements of Statistical Learning